Menu Close

solve-y-2y-y-x-1-2-e-x-with-y-0-1-y-0-0-y-2-0-1-

Tinku Tara 0 Comments
Pin




Question Number 96571 by mathmax by abdo last updated on 02/Jun/20
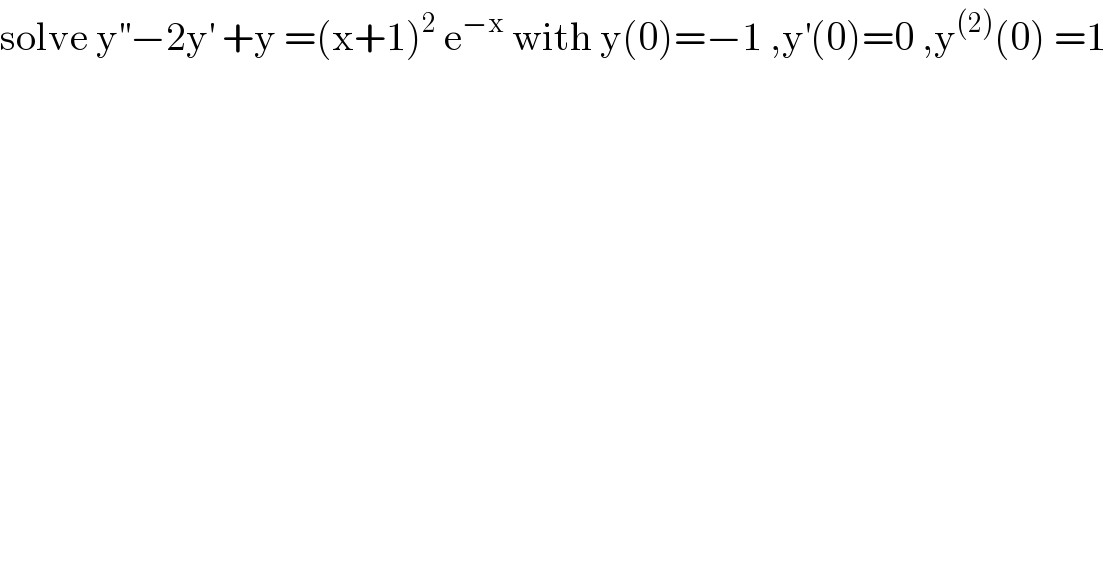
solve y^(′′) −2y^′ +y =(x+1)^2 e^(−x) with y(0)=−1 ,y^′ (0)=0 ,y^((2)) (0) =1
$$\mathrm{solve}\:\mathrm{y}^{''} −\mathrm{2y}^{'} \:+\mathrm{y}\:=\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} \:\mathrm{e}^{−\mathrm{x}} \:\mathrm{with}\:\mathrm{y}\left(\mathrm{0}\right)=−\mathrm{1}\:,\mathrm{y}^{'} \left(\mathrm{0}\right)=\mathrm{0}\:,\mathrm{y}^{\left(\mathrm{2}\right)} \left(\mathrm{0}\right)\:=\mathrm{1} \\ $$
Answered by mathmax by abdo last updated on 03/Jun/20
let solve by laplace transform (e)⇒L(y^(′′) )−2L(y^′ )+L(y) =L((x+1)^2 e^(−x) ) ⇒ x^2 L(y)−x y(0)−y^′ (0)−2(xL(y)−y(o))+L(y) =L{(x+1)^2 e^(−x) } ⇒ (x^2 −2x+1)L(y)+x−2 =L{(x+1)^2 e^(−x) } ⇒ (x^2 −2x+1)L(y)=−x+2 +L{(x+1)^2 e^(−x) } L{(x+1)^2 e^(−x) } =∫_0 ^∞ (t+1)^2 e^(−t) e^(−xt) dt =∫_0 ^∞ (t+1)^2 e^(−(x+1)t) dt =_(by parts) [(((t+1)^2 )/(−(x+1))) e^(−(x+1)t) ]_0 ^∞ −∫_0 ^∞ 2(t+1)×(1/(−(x+1)))e^(−(x+1)t) dt =(1/(x+1)) +(2/(x+1))∫_0 ^∞ (t+1)e^(−(x+1)t) [dt =(1/(x+1)) +(2/(x+1)){ [((t+1)/(−(x+1)))e^(−(x+1)t) ]_0 ^∞ −∫_0 ^∞ (1/(−(x+1)))e^(−(x+1)t) dt} =(1/(x+1)) +(2/(x+1)){ (1/(x+1)) +(1/(x+1))[(1/(−(x+1)))e^(−(x+1)t) ]_0 ^∞ } =(1/(x+1)) +(2/((x+1)^2 )){ 1+(1/(x+1))} =(1/(x+1)) +(2/((x+1)^2 )) +(2/((x+1)^3 )) (e)⇒(x^2 −2x+1)L(y) =−x+2 +(1/(x+1)) +(2/((x+1)^2 )) +(2/((x+1)^3 )) ⇒ L(y) =((−x+2)/(x^2 −2x+1)) +(1/((x+1)(x^2 −2x+1))) +(2/((x+1)^2 (x^2 −2x+1))) +(2/((x+1)^3 (x^2 −2x+1))) =((−x+2)/((x−1)^2 )) +(1/((x+1)(x−1)^2 )) +(2/((x+1)^2 (x−1)^2 )) +(2/((x+1)^3 (x−1)^2 )) ⇒ y =L^(−1) (((−x+2)/((x−1)^2 )))+L^(−1) ((1/((x+1)(x−1)^2 )))+L^(−1) ((2/((x+1)^( (x−1)^2 ))) +L^(−1) ((2/((x+1)^3 (x−1)^2 ))) ...be continued...
$$\mathrm{let}\:\mathrm{solve}\:\mathrm{by}\:\mathrm{laplace}\:\mathrm{transform}\: \\ $$$$\left(\mathrm{e}\right)\Rightarrow\mathrm{L}\left(\mathrm{y}^{''} \right)−\mathrm{2L}\left(\mathrm{y}^{'} \right)+\mathrm{L}\left(\mathrm{y}\right)\:=\mathrm{L}\left(\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} \:\mathrm{e}^{−\mathrm{x}} \right)\:\Rightarrow \\ $$$$\mathrm{x}^{\mathrm{2}} \:\mathrm{L}\left(\mathrm{y}\right)−\mathrm{x}\:\mathrm{y}\left(\mathrm{0}\right)−\mathrm{y}^{'} \left(\mathrm{0}\right)−\mathrm{2}\left(\mathrm{xL}\left(\mathrm{y}\right)−\mathrm{y}\left(\mathrm{o}\right)\right)+\mathrm{L}\left(\mathrm{y}\right)\:=\mathrm{L}\left\{\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} \:\mathrm{e}^{−\mathrm{x}} \right\}\:\Rightarrow \\ $$$$\left(\mathrm{x}^{\mathrm{2}} −\mathrm{2x}+\mathrm{1}\right)\mathrm{L}\left(\mathrm{y}\right)+\mathrm{x}−\mathrm{2}\:=\mathrm{L}\left\{\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} \:\mathrm{e}^{−\mathrm{x}} \right\}\:\Rightarrow \\ $$$$\left(\mathrm{x}^{\mathrm{2}} −\mathrm{2x}+\mathrm{1}\right)\mathrm{L}\left(\mathrm{y}\right)=−\mathrm{x}+\mathrm{2}\:+\mathrm{L}\left\{\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} \:\mathrm{e}^{−\mathrm{x}} \right\} \\ $$$$\mathrm{L}\left\{\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} \:\mathrm{e}^{−\mathrm{x}} \right\}\:=\int_{\mathrm{0}} ^{\infty} \:\left(\mathrm{t}+\mathrm{1}\right)^{\mathrm{2}} \:\mathrm{e}^{−\mathrm{t}} \:\mathrm{e}^{−\mathrm{xt}} \:\mathrm{dt}\:=\int_{\mathrm{0}} ^{\infty} \:\left(\mathrm{t}+\mathrm{1}\right)^{\mathrm{2}} \:\mathrm{e}^{−\left(\mathrm{x}+\mathrm{1}\right)\mathrm{t}} \:\mathrm{dt} \\ $$$$=_{\mathrm{by}\:\mathrm{parts}} \:\:\:\:\left[\frac{\left(\mathrm{t}+\mathrm{1}\right)^{\mathrm{2}} }{−\left(\mathrm{x}+\mathrm{1}\right)}\:\mathrm{e}^{−\left(\mathrm{x}+\mathrm{1}\right)\mathrm{t}} \right]_{\mathrm{0}} ^{\infty} \:−\int_{\mathrm{0}} ^{\infty} \:\mathrm{2}\left(\mathrm{t}+\mathrm{1}\right)×\frac{\mathrm{1}}{−\left(\mathrm{x}+\mathrm{1}\right)}\mathrm{e}^{−\left(\mathrm{x}+\mathrm{1}\right)\mathrm{t}} \:\mathrm{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{x}+\mathrm{1}}\:+\frac{\mathrm{2}}{\mathrm{x}+\mathrm{1}}\int_{\mathrm{0}} ^{\infty} \:\:\left(\mathrm{t}+\mathrm{1}\right)\mathrm{e}^{−\left(\mathrm{x}+\mathrm{1}\right)\mathrm{t}} \left[\mathrm{dt}\right. \\ $$$$=\frac{\mathrm{1}}{\mathrm{x}+\mathrm{1}}\:+\frac{\mathrm{2}}{\mathrm{x}+\mathrm{1}}\left\{\:\:\left[\frac{\mathrm{t}+\mathrm{1}}{−\left(\mathrm{x}+\mathrm{1}\right)}\mathrm{e}^{−\left(\mathrm{x}+\mathrm{1}\right)\mathrm{t}} \right]_{\mathrm{0}} ^{\infty} \:−\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{−\left(\mathrm{x}+\mathrm{1}\right)}\mathrm{e}^{−\left(\mathrm{x}+\mathrm{1}\right)\mathrm{t}} \mathrm{dt}\right\} \\ $$$$=\frac{\mathrm{1}}{\mathrm{x}+\mathrm{1}}\:+\frac{\mathrm{2}}{\mathrm{x}+\mathrm{1}}\left\{\:\frac{\mathrm{1}}{\mathrm{x}+\mathrm{1}}\:+\frac{\mathrm{1}}{\mathrm{x}+\mathrm{1}}\left[\frac{\mathrm{1}}{−\left(\mathrm{x}+\mathrm{1}\right)}\mathrm{e}^{−\left(\mathrm{x}+\mathrm{1}\right)\mathrm{t}} \right]_{\mathrm{0}} ^{\infty} \right\} \\ $$$$=\frac{\mathrm{1}}{\mathrm{x}+\mathrm{1}}\:+\frac{\mathrm{2}}{\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} }\left\{\:\mathrm{1}+\frac{\mathrm{1}}{\mathrm{x}+\mathrm{1}}\right\}\:=\frac{\mathrm{1}}{\mathrm{x}+\mathrm{1}}\:+\frac{\mathrm{2}}{\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} }\:+\frac{\mathrm{2}}{\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{3}} } \\ $$$$\left(\mathrm{e}\right)\Rightarrow\left(\mathrm{x}^{\mathrm{2}} −\mathrm{2x}+\mathrm{1}\right)\mathrm{L}\left(\mathrm{y}\right)\:=−\mathrm{x}+\mathrm{2}\:+\frac{\mathrm{1}}{\mathrm{x}+\mathrm{1}}\:+\frac{\mathrm{2}}{\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} }\:+\frac{\mathrm{2}}{\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{3}} }\:\Rightarrow \\ $$$$\mathrm{L}\left(\mathrm{y}\right)\:=\frac{−\mathrm{x}+\mathrm{2}}{\mathrm{x}^{\mathrm{2}} −\mathrm{2x}+\mathrm{1}}\:+\frac{\mathrm{1}}{\left(\mathrm{x}+\mathrm{1}\right)\left(\mathrm{x}^{\mathrm{2}} −\mathrm{2x}+\mathrm{1}\right)}\:+\frac{\mathrm{2}}{\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} \left(\mathrm{x}^{\mathrm{2}} −\mathrm{2x}+\mathrm{1}\right)}\:+\frac{\mathrm{2}}{\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{3}} \left(\mathrm{x}^{\mathrm{2}} −\mathrm{2x}+\mathrm{1}\right)} \\ $$$$=\frac{−\mathrm{x}+\mathrm{2}}{\left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{2}} }\:+\frac{\mathrm{1}}{\left(\mathrm{x}+\mathrm{1}\right)\left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{2}} }\:+\frac{\mathrm{2}}{\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} \left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{2}} }\:+\frac{\mathrm{2}}{\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{3}} \left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{2}} }\:\Rightarrow \\ $$$$\mathrm{y}\:=\mathrm{L}^{−\mathrm{1}} \left(\frac{−\mathrm{x}+\mathrm{2}}{\left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{2}} }\right)+\mathrm{L}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\left(\mathrm{x}+\mathrm{1}\right)\left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{2}} }\right)+\mathrm{L}^{−\mathrm{1}} \left(\frac{\mathrm{2}}{\left(\mathrm{x}+\mathrm{1}\right)^{\left(\right.} \left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{2}} }\right)\:+\mathrm{L}^{−\mathrm{1}} \left(\frac{\mathrm{2}}{\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{3}} \left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{2}} }\right) \\ $$$$…\mathrm{be}\:\mathrm{continued}… \\ $$
Answered by mathmax by abdo last updated on 03/Jun/20
wronkien method (he)→y^((2)) −2y^((1)) +y =0→r^2 −2r +1 =0 ⇒(r−1)^2 =0 ⇒ r=1 ⇒y_h =(ax+b)e^x =axe^x +be^x =au_1 +bu_2 ,u_1 =xe^x and u_2 =e^x W(u_1 ,u_2 ) = determinant (((u_1 u_2 )),((u_1 ^′ u_2 ^′ )))= determinant (((xe^x e^x )),(((x+1)e^x e^x )))=xe^(2x) −(x+1)e^(2x) =−e^(2x) W_1 = determinant (((0 e^x )),(((x+1)^2 e^(−x) e^x )))=−(x+1)^2 W_2 = determinant (((xe^x 0)),(((x+1)e^x (x+1)^2 e^(−x) )))=x(x+1)^2 v_1 =∫ (w_1 /W)dx =∫ ((−(x+1)^2 )/(−e^(2x) )) dx =∫ (x+1)^2 e^(−2x) dx =−(1/2)(x+1)^2 e^(−2x) −∫ 2(x+1)×(−(1/2))e^(−2x) dx =−(1/2)(x+1)^2 e^(−2x) +∫ (x+1)e^(−2x) dx =−(1/2)(x+1)^2 −((x+1)/2) e^(−2x) +(1/2)∫ e^(−2x) dx =−(((x+1)^2 )/2)−(((x+1)e^(−2x) )/2) −(1/4) e^(−2x) v_2 =∫ ((w2)/W)dx =∫ ((x(x+1)^2 )/(−e^(2x) ))dx =−∫ x(x^2 +2x+1)e^(−2x) dx −v_2 =∫ (x^3 +2x^2 +x)e^(−2x) dx =−(1/2)(x^3 +2x^2 +x)e^(−2x) +(1/2)∫ (3x^2 +4x+1)e^(−2x) dx =−(1/2)(x^3 +2x^2 +x)e^(−2x) +(1/2)( −(1/2)(3x^2 +4x+1)e^(−2x) +(1/2)∫(6x+4)e^(−2x) dx) =−(1/2)(x^3 +2x^2 +x)e^(−2x) −(1/4)(3x^2 +4x+1)e^(−2x) +(1/2)∫ (3x+2)e^(−2x) dx but ∫ (3x+2)e^(−2x) dx =−(1/2)(3x+2)e^(−2x) +(3/2)∫ e^(−2x) dx =−(1/2)(3x+2)e^(−2x) −(3/4)e^(−2x) ⇒ v_2 =((1/2)(x^3 +2x^2 +x) +(1/4)(3x^2 +4x+1)+(1/2)(3x+2)+(3/4))e^(−2x) =.... y_p =u_1 v_1 +u_2 v_(2 ) and general solution is y =y_h +y_p ...be continued....
$$\mathrm{wronkien}\:\mathrm{method}\:\:\left(\mathrm{he}\right)\rightarrow\mathrm{y}^{\left(\mathrm{2}\right)} −\mathrm{2y}^{\left(\mathrm{1}\right)} \:+\mathrm{y}\:=\mathrm{0}\rightarrow\mathrm{r}^{\mathrm{2}} −\mathrm{2r}\:+\mathrm{1}\:=\mathrm{0}\:\Rightarrow\left(\mathrm{r}−\mathrm{1}\right)^{\mathrm{2}} \:=\mathrm{0}\:\Rightarrow \\ $$$$\mathrm{r}=\mathrm{1}\:\Rightarrow\mathrm{y}_{\mathrm{h}} =\left(\mathrm{ax}+\mathrm{b}\right)\mathrm{e}^{\mathrm{x}} \:=\mathrm{axe}^{\mathrm{x}} \:+\mathrm{be}^{\mathrm{x}} \:=\mathrm{au}_{\mathrm{1}} \:+\mathrm{bu}_{\mathrm{2}} \:\:\:\:,\mathrm{u}_{\mathrm{1}} =\mathrm{xe}^{\mathrm{x}} \:\mathrm{and}\:\mathrm{u}_{\mathrm{2}} =\mathrm{e}^{\mathrm{x}} \\ $$$$\mathrm{W}\left(\mathrm{u}_{\mathrm{1}} \:,\mathrm{u}_{\mathrm{2}} \right)\:=\begin{vmatrix}{\mathrm{u}_{\mathrm{1}} \:\:\:\:\:\:\:\:\:\mathrm{u}_{\mathrm{2}} }\\{\mathrm{u}_{\mathrm{1}} ^{'} \:\:\:\:\:\:\:\:\:\mathrm{u}_{\mathrm{2}} ^{'} }\end{vmatrix}=\begin{vmatrix}{\mathrm{xe}^{\mathrm{x}} \:\:\:\:\:\:\:\:\:\:\:\:\mathrm{e}^{\mathrm{x}} }\\{\left(\mathrm{x}+\mathrm{1}\right)\mathrm{e}^{\mathrm{x}} \:\:\:\mathrm{e}^{\mathrm{x}} }\end{vmatrix}=\mathrm{xe}^{\mathrm{2x}} −\left(\mathrm{x}+\mathrm{1}\right)\mathrm{e}^{\mathrm{2x}} \:=−\mathrm{e}^{\mathrm{2x}} \\ $$$$\mathrm{W}_{\mathrm{1}} =\begin{vmatrix}{\mathrm{0}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{e}^{\mathrm{x}} }\\{\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} \mathrm{e}^{−\mathrm{x}} \:\:\:\:\mathrm{e}^{\mathrm{x}} }\end{vmatrix}=−\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} \\ $$$$\mathrm{W}_{\mathrm{2}} =\begin{vmatrix}{\mathrm{xe}^{\mathrm{x}} \:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{0}}\\{\left(\mathrm{x}+\mathrm{1}\right)\mathrm{e}^{\mathrm{x}} \:\:\:\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} \mathrm{e}^{−\mathrm{x}} }\end{vmatrix}=\mathrm{x}\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} \\ $$$$\mathrm{v}_{\mathrm{1}} =\int\:\frac{\mathrm{w}_{\mathrm{1}} }{\mathrm{W}}\mathrm{dx}\:=\int\:\:\frac{−\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} }{−\mathrm{e}^{\mathrm{2x}} }\:\mathrm{dx}\:=\int\:\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} \:\mathrm{e}^{−\mathrm{2x}} \:\mathrm{dx} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} \:\mathrm{e}^{−\mathrm{2x}} −\int\:\mathrm{2}\left(\mathrm{x}+\mathrm{1}\right)×\left(−\frac{\mathrm{1}}{\mathrm{2}}\right)\mathrm{e}^{−\mathrm{2x}} \:\mathrm{dx} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} \:\mathrm{e}^{−\mathrm{2x}} \:+\int\:\left(\mathrm{x}+\mathrm{1}\right)\mathrm{e}^{−\mathrm{2x}} \:\mathrm{dx} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} \:−\frac{\mathrm{x}+\mathrm{1}}{\mathrm{2}}\:\mathrm{e}^{−\mathrm{2x}} +\frac{\mathrm{1}}{\mathrm{2}}\int\:\:\mathrm{e}^{−\mathrm{2x}} \:\mathrm{dx} \\ $$$$=−\frac{\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{2}}−\frac{\left(\mathrm{x}+\mathrm{1}\right)\mathrm{e}^{−\mathrm{2x}} }{\mathrm{2}}\:−\frac{\mathrm{1}}{\mathrm{4}}\:\mathrm{e}^{−\mathrm{2x}} \\ $$$$\mathrm{v}_{\mathrm{2}} =\int\:\frac{\mathrm{w2}}{\mathrm{W}}\mathrm{dx}\:=\int\:\:\frac{\mathrm{x}\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} }{−\mathrm{e}^{\mathrm{2x}} }\mathrm{dx}\:=−\int\:\mathrm{x}\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{2x}+\mathrm{1}\right)\mathrm{e}^{−\mathrm{2x}} \:\mathrm{dx} \\ $$$$−\mathrm{v}_{\mathrm{2}} =\int\:\:\left(\mathrm{x}^{\mathrm{3}} \:+\mathrm{2x}^{\mathrm{2}} \:+\mathrm{x}\right)\mathrm{e}^{−\mathrm{2x}} \:\mathrm{dx} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{x}^{\mathrm{3}} \:+\mathrm{2x}^{\mathrm{2}} \:+\mathrm{x}\right)\mathrm{e}^{−\mathrm{2x}} \:+\frac{\mathrm{1}}{\mathrm{2}}\int\:\left(\mathrm{3x}^{\mathrm{2}} \:+\mathrm{4x}+\mathrm{1}\right)\mathrm{e}^{−\mathrm{2x}} \mathrm{dx} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{x}^{\mathrm{3}} \:+\mathrm{2x}^{\mathrm{2}} +\mathrm{x}\right)\mathrm{e}^{−\mathrm{2x}} \:+\frac{\mathrm{1}}{\mathrm{2}}\left(\:\:−\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{3x}^{\mathrm{2}} \:+\mathrm{4x}+\mathrm{1}\right)\mathrm{e}^{−\mathrm{2x}} +\frac{\mathrm{1}}{\mathrm{2}}\int\left(\mathrm{6x}+\mathrm{4}\right)\mathrm{e}^{−\mathrm{2x}} \mathrm{dx}\right) \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{x}^{\mathrm{3}} \:+\mathrm{2x}^{\mathrm{2}} \:+\mathrm{x}\right)\mathrm{e}^{−\mathrm{2x}} −\frac{\mathrm{1}}{\mathrm{4}}\left(\mathrm{3x}^{\mathrm{2}} \:+\mathrm{4x}+\mathrm{1}\right)\mathrm{e}^{−\mathrm{2x}} +\frac{\mathrm{1}}{\mathrm{2}}\int\:\left(\mathrm{3x}+\mathrm{2}\right)\mathrm{e}^{−\mathrm{2x}} \:\mathrm{dx}\:\mathrm{but} \\ $$$$\int\:\left(\mathrm{3x}+\mathrm{2}\right)\mathrm{e}^{−\mathrm{2x}} \:\mathrm{dx}\:=−\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{3x}+\mathrm{2}\right)\mathrm{e}^{−\mathrm{2x}} \:+\frac{\mathrm{3}}{\mathrm{2}}\int\:\:\mathrm{e}^{−\mathrm{2x}} \:\mathrm{dx} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{3x}+\mathrm{2}\right)\mathrm{e}^{−\mathrm{2x}} \:−\frac{\mathrm{3}}{\mathrm{4}}\mathrm{e}^{−\mathrm{2x}} \:\Rightarrow \\ $$$$\mathrm{v}_{\mathrm{2}} =\left(\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{x}^{\mathrm{3}} \:+\mathrm{2x}^{\mathrm{2}} \:+\mathrm{x}\right)\:+\frac{\mathrm{1}}{\mathrm{4}}\left(\mathrm{3x}^{\mathrm{2}} \:+\mathrm{4x}+\mathrm{1}\right)+\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{3x}+\mathrm{2}\right)+\frac{\mathrm{3}}{\mathrm{4}}\right)\mathrm{e}^{−\mathrm{2x}} \:=…. \\ $$$$\mathrm{y}_{\mathrm{p}} =\mathrm{u}_{\mathrm{1}} \mathrm{v}_{\mathrm{1}} \:+\mathrm{u}_{\mathrm{2}} \mathrm{v}_{\mathrm{2}\:\:} \:\:\mathrm{and}\:\mathrm{general}\:\mathrm{solution}\:\mathrm{is} \\ $$$$\mathrm{y}\:=\mathrm{y}_{\mathrm{h}} \:+\mathrm{y}_{\mathrm{p}} …\mathrm{be}\:\mathrm{continued}…. \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *