Question Number 129130 by bounhome last updated on 13/Jan/21
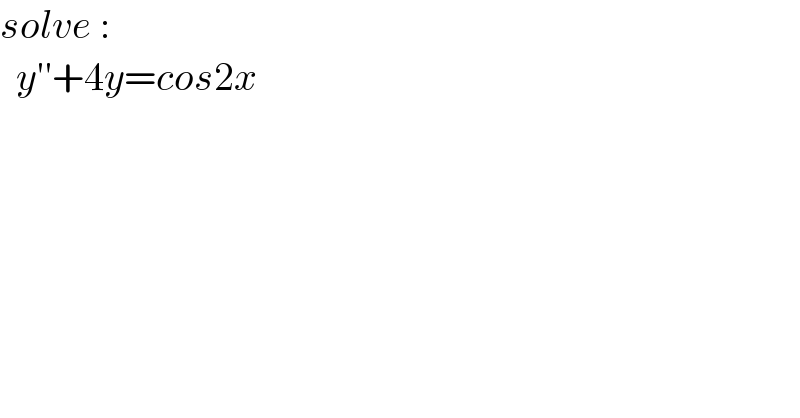
$${solve}\:: \\ $$$$\:\:{y}''+\mathrm{4}{y}={cos}\mathrm{2}{x} \\ $$$$\: \\ $$
Answered by liberty last updated on 13/Jan/21

$$\:\mathrm{Homogenous}\:\mathrm{solution}\:\mathrm{y}_{\mathrm{h}} =\mathrm{C}_{\mathrm{1}} \mathrm{cos}\:\mathrm{2x}+\mathrm{C}_{\mathrm{2}} \mathrm{sin}\:\mathrm{2x} \\ $$$$\mathrm{W}\left(\bar {\mathrm{u}}_{\mathrm{1}} \mathrm{u}_{\mathrm{2}} \right)=\begin{vmatrix}{\mathrm{cos}\:\mathrm{2x}\:\:\:\:\:\:\:\mathrm{sin}\:\mathrm{2x}}\\{−\mathrm{2sin}\:\mathrm{2x}\:\:\:\mathrm{2cos}\:\mathrm{2x}}\end{vmatrix}=\mathrm{2} \\ $$$$\:\mathrm{W}_{\mathrm{1}} =\begin{vmatrix}{\mathrm{0}\:\:\:\:\:\:\:\:\:\:\mathrm{sin}\:\mathrm{2x}}\\{\mathrm{cos}\:\mathrm{2x}\:\:\:\mathrm{2cos}\:\mathrm{2x}}\end{vmatrix}=−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\:\mathrm{4x} \\ $$$$\:\mathrm{W}_{\mathrm{2}} =\begin{vmatrix}{\mathrm{cos}\:\mathrm{2x}\:\:\:\:\:\:\:\:\:\:\:\mathrm{0}}\\{−\mathrm{2sin}\:\mathrm{2x}\:\:\:\:\mathrm{cos}\:\mathrm{2x}}\end{vmatrix}=\:\mathrm{cos}\:^{\mathrm{2}} \mathrm{2x} \\ $$$$\:\mathrm{v}_{\mathrm{1}} =\int\frac{\mathrm{W}_{\mathrm{1}} }{\mathrm{W}}\:\mathrm{dx}\:=\:\frac{\mathrm{1}}{\mathrm{16}}\mathrm{cos}\:\mathrm{4x} \\ $$$$\:\mathrm{v}_{\mathrm{2}} =\int\frac{\mathrm{W}_{\mathrm{2}} }{\mathrm{W}}\:\mathrm{dx}=\frac{\mathrm{1}}{\mathrm{4}}\mathrm{x}+\frac{\mathrm{1}}{\mathrm{16}}\mathrm{sin}\:\mathrm{4x} \\ $$$$\mathrm{y}_{\mathrm{p}} =\:\frac{\mathrm{1}}{\mathrm{16}}\mathrm{cos}\:\mathrm{4x}\:\mathrm{cos}\:\mathrm{2x}+\left(\frac{\mathrm{1}}{\mathrm{4}}\mathrm{x}+\frac{\mathrm{1}}{\mathrm{16}}\mathrm{sin}\:\mathrm{4x}\right)\mathrm{sin}\:\mathrm{2x} \\ $$$$\mathrm{y}_{\mathrm{p}} =\frac{\mathrm{1}}{\mathrm{16}}\mathrm{cos}\:\mathrm{2x}+\frac{\mathrm{1}}{\mathrm{4}}\mathrm{x}\:\mathrm{sin}\:\mathrm{2x} \\ $$$$\mathrm{General}\:\mathrm{solution} \\ $$$$\mathrm{y}_{\mathrm{G}} \:=\:\left(\mathrm{C}_{\mathrm{1}} +\frac{\mathrm{1}}{\mathrm{16}}\right)\mathrm{cos}\:\mathrm{2x}+\left(\mathrm{C}_{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{4}}\mathrm{x}\right)\mathrm{sin}\:\mathrm{2x} \\ $$
