Menu Close

solve-y-5y-3y-x-2-sin-3x-with-y-0-0-and-y-0-1-

Tinku Tara 0 Comments
Pin




Question Number 99113 by mathmax by abdo last updated on 18/Jun/20
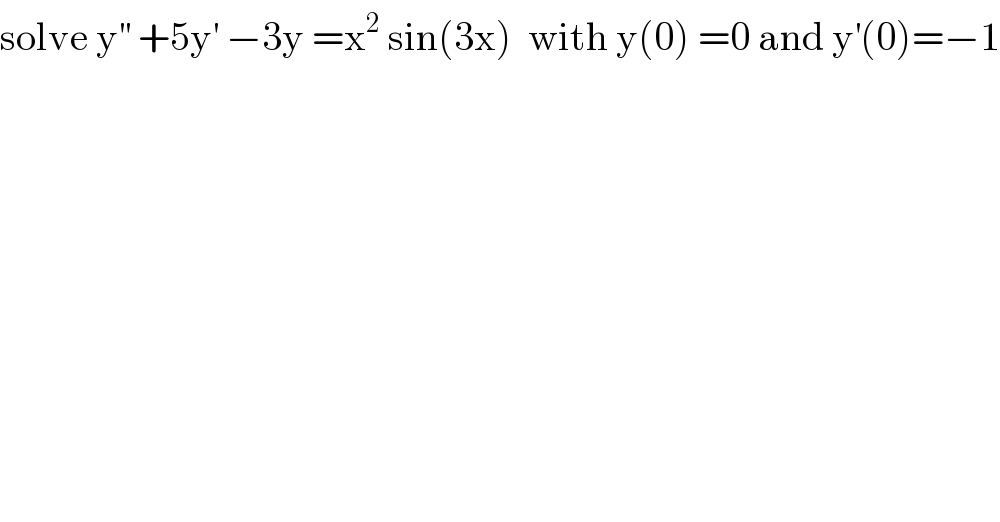
solve y^(′′) +5y^′ −3y =x^2 sin(3x) with y(0) =0 and y^′ (0)=−1
$$\mathrm{solve}\:\mathrm{y}^{''} \:+\mathrm{5y}^{'} \:−\mathrm{3y}\:=\mathrm{x}^{\mathrm{2}} \:\mathrm{sin}\left(\mathrm{3x}\right)\:\:\mathrm{with}\:\mathrm{y}\left(\mathrm{0}\right)\:=\mathrm{0}\:\mathrm{and}\:\mathrm{y}^{'} \left(\mathrm{0}\right)=−\mathrm{1} \\ $$
Answered by mathmax by abdo last updated on 19/Jun/20
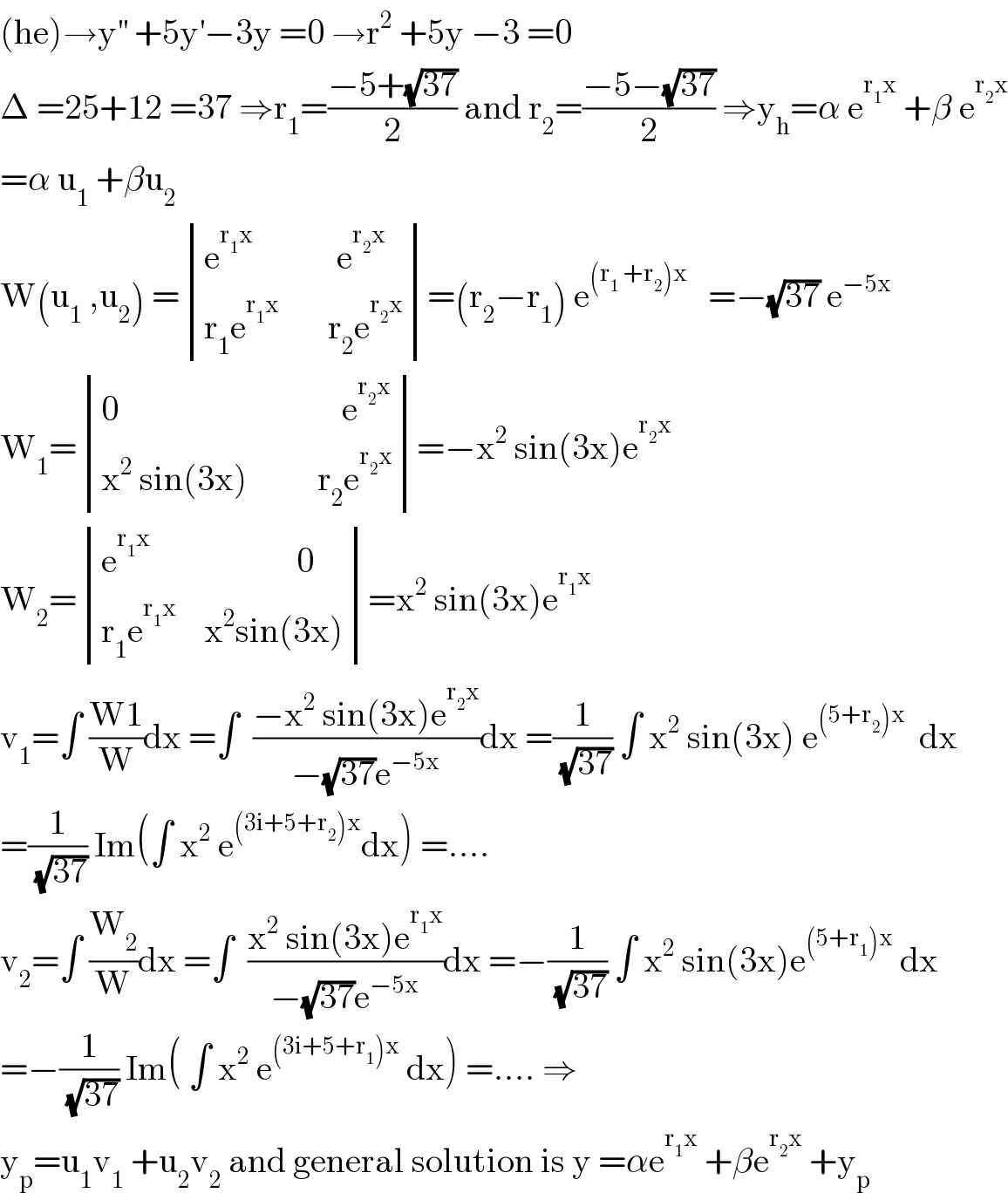
(he)→y^(′′) +5y^′ −3y =0 →r^2 +5y −3 =0 Δ =25+12 =37 ⇒r_1 =((−5+(√(37)))/2) and r_2 =((−5−(√(37)))/2) ⇒y_h =α e^(r_1 x) +β e^(r_2 x) =α u_1 +βu_2 W(u_1 ,u_2 ) = determinant (((e^(r_1 x) e^(r_2 x) )),((r_1 e^(r_1 x) r_2 e^(r_2 x) )))=(r_2 −r_1 ) e^((r_1 +r_2 )x) =−(√(37)) e^(−5x) W_1 = determinant (((0 e^(r_2 x) )),((x^2 sin(3x) r_2 e^(r_2 x) )))=−x^2 sin(3x)e^(r_2 x) W_2 = determinant (((e^(r_1 x) 0)),((r_1 e^(r_1 x) x^2 sin(3x))))=x^2 sin(3x)e^(r_1 x) v_1 =∫ ((W1)/W)dx =∫ ((−x^2 sin(3x)e^(r_2 x) )/(−(√(37))e^(−5x) ))dx =(1/( (√(37)))) ∫ x^2 sin(3x) e^((5+r_2 )x) dx =(1/( (√(37)))) Im(∫ x^2 e^((3i+5+r_2 )x) dx) =.... v_2 =∫ (W_2 /W)dx =∫ ((x^2 sin(3x)e^(r_1 x) )/(−(√(37))e^(−5x) ))dx =−(1/( (√(37)))) ∫ x^2 sin(3x)e^((5+r_1 )x) dx =−(1/( (√(37)))) Im( ∫ x^2 e^((3i+5+r_1 )x) dx) =.... ⇒ y_p =u_1 v_1 +u_2 v_2 and general solution is y =αe^(r_1 x) +βe^(r_2 x) +y_p
$$\left(\mathrm{he}\right)\rightarrow\mathrm{y}^{''} \:+\mathrm{5y}^{'} −\mathrm{3y}\:=\mathrm{0}\:\rightarrow\mathrm{r}^{\mathrm{2}} \:+\mathrm{5y}\:−\mathrm{3}\:=\mathrm{0} \\ $$$$\Delta\:=\mathrm{25}+\mathrm{12}\:=\mathrm{37}\:\Rightarrow\mathrm{r}_{\mathrm{1}} =\frac{−\mathrm{5}+\sqrt{\mathrm{37}}}{\mathrm{2}}\:\mathrm{and}\:\mathrm{r}_{\mathrm{2}} =\frac{−\mathrm{5}−\sqrt{\mathrm{37}}}{\mathrm{2}}\:\Rightarrow\mathrm{y}_{\mathrm{h}} =\alpha\:\mathrm{e}^{\mathrm{r}_{\mathrm{1}} \mathrm{x}} \:+\beta\:\mathrm{e}^{\mathrm{r}_{\mathrm{2}} \mathrm{x}} \\ $$$$=\alpha\:\mathrm{u}_{\mathrm{1}} \:+\beta\mathrm{u}_{\mathrm{2}} \\ $$$$\mathrm{W}\left(\mathrm{u}_{\mathrm{1}} \:,\mathrm{u}_{\mathrm{2}} \right)\:=\begin{vmatrix}{\mathrm{e}^{\mathrm{r}_{\mathrm{1}} \mathrm{x}} \:\:\:\:\:\:\:\:\:\:\:\:\mathrm{e}^{\mathrm{r}_{\mathrm{2}} \mathrm{x}} }\\{\mathrm{r}_{\mathrm{1}} \mathrm{e}^{\mathrm{r}_{\mathrm{1}} \mathrm{x}} \:\:\:\:\:\:\:\mathrm{r}_{\mathrm{2}} \mathrm{e}^{\mathrm{r}_{\mathrm{2}} \mathrm{x}} }\end{vmatrix}=\left(\mathrm{r}_{\mathrm{2}} −\mathrm{r}_{\mathrm{1}} \right)\:\mathrm{e}^{\left(\mathrm{r}_{\mathrm{1}} \:+\mathrm{r}_{\mathrm{2}} \right)\mathrm{x}} \:\:\:=−\sqrt{\mathrm{37}}\:\mathrm{e}^{−\mathrm{5x}} \: \\ $$$$\mathrm{W}_{\mathrm{1}} =\begin{vmatrix}{\mathrm{0}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{e}^{\mathrm{r}_{\mathrm{2}} \mathrm{x}} }\\{\mathrm{x}^{\mathrm{2}} \:\mathrm{sin}\left(\mathrm{3x}\right)\:\:\:\:\:\:\:\:\:\:\mathrm{r}_{\mathrm{2}} \mathrm{e}^{\mathrm{r}_{\mathrm{2}} \mathrm{x}} }\end{vmatrix}=−\mathrm{x}^{\mathrm{2}} \:\mathrm{sin}\left(\mathrm{3x}\right)\mathrm{e}^{\mathrm{r}_{\mathrm{2}} \mathrm{x}} \\ $$$$\mathrm{W}_{\mathrm{2}} =\begin{vmatrix}{\mathrm{e}^{\mathrm{r}_{\mathrm{1}} \mathrm{x}} \:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{0}}\\{\mathrm{r}_{\mathrm{1}} \mathrm{e}^{\mathrm{r}_{\mathrm{1}} \mathrm{x}} \:\:\:\:\mathrm{x}^{\mathrm{2}} \mathrm{sin}\left(\mathrm{3x}\right)}\end{vmatrix}=\mathrm{x}^{\mathrm{2}} \:\mathrm{sin}\left(\mathrm{3x}\right)\mathrm{e}^{\mathrm{r}_{\mathrm{1}} \mathrm{x}} \\ $$$$\mathrm{v}_{\mathrm{1}} =\int\:\frac{\mathrm{W1}}{\mathrm{W}}\mathrm{dx}\:=\int\:\:\frac{−\mathrm{x}^{\mathrm{2}} \:\mathrm{sin}\left(\mathrm{3x}\right)\mathrm{e}^{\mathrm{r}_{\mathrm{2}} \mathrm{x}} }{−\sqrt{\mathrm{37}}\mathrm{e}^{−\mathrm{5x}} }\mathrm{dx}\:=\frac{\mathrm{1}}{\:\sqrt{\mathrm{37}}}\:\int\:\mathrm{x}^{\mathrm{2}} \:\mathrm{sin}\left(\mathrm{3x}\right)\:\mathrm{e}^{\left(\mathrm{5}+\mathrm{r}_{\mathrm{2}} \right)\mathrm{x}} \:\:\mathrm{dx} \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{\mathrm{37}}}\:\mathrm{Im}\left(\int\:\mathrm{x}^{\mathrm{2}} \:\mathrm{e}^{\left(\mathrm{3i}+\mathrm{5}+\mathrm{r}_{\mathrm{2}} \right)\mathrm{x}} \mathrm{dx}\right)\:=…. \\ $$$$\mathrm{v}_{\mathrm{2}} =\int\:\frac{\mathrm{W}_{\mathrm{2}} }{\mathrm{W}}\mathrm{dx}\:=\int\:\:\frac{\mathrm{x}^{\mathrm{2}} \:\mathrm{sin}\left(\mathrm{3x}\right)\mathrm{e}^{\mathrm{r}_{\mathrm{1}} \mathrm{x}} }{−\sqrt{\mathrm{37}}\mathrm{e}^{−\mathrm{5x}} }\mathrm{dx}\:=−\frac{\mathrm{1}}{\:\sqrt{\mathrm{37}}}\:\int\:\mathrm{x}^{\mathrm{2}} \:\mathrm{sin}\left(\mathrm{3x}\right)\mathrm{e}^{\left(\mathrm{5}+\mathrm{r}_{\mathrm{1}} \right)\mathrm{x}} \:\mathrm{dx} \\ $$$$=−\frac{\mathrm{1}}{\:\sqrt{\mathrm{37}}}\:\mathrm{Im}\left(\:\int\:\mathrm{x}^{\mathrm{2}} \:\mathrm{e}^{\left(\mathrm{3i}+\mathrm{5}+\mathrm{r}_{\mathrm{1}} \right)\mathrm{x}} \:\mathrm{dx}\right)\:=….\:\Rightarrow \\ $$$$\mathrm{y}_{\mathrm{p}} =\mathrm{u}_{\mathrm{1}} \mathrm{v}_{\mathrm{1}} \:+\mathrm{u}_{\mathrm{2}} \mathrm{v}_{\mathrm{2}} \:\mathrm{and}\:\mathrm{general}\:\mathrm{solution}\:\mathrm{is}\:\mathrm{y}\:=\alpha\mathrm{e}^{\mathrm{r}_{\mathrm{1}} \mathrm{x}} \:+\beta\mathrm{e}^{\mathrm{r}_{\mathrm{2}} \mathrm{x}} \:+\mathrm{y}_{\mathrm{p}} \\ $$
Answered by mathmax by abdo last updated on 20/Jun/20
let take a try with laplace transform e ⇒L(y^(′′) )+5L(y^′ )−3L(y) =L(x^2 sin(3x)) ⇒ x^2 L(y)−xy(0)−y^′ (0)+5(x L(y)−y(0))−3L(y) =L(x^2 sin(3x)) ⇒ (x^2 +5x−3)L(y) +1 =L(x^2 sin(3x) we have L(x^2 sin(3x)) =∫_0 ^∞ t^2 sin(3t) e^(−xt) dt =Im(∫_0 ^∞ t^2 e^((3i−x)t) dt) ∫_0 ^∞ t^2 e^((−x+3i)t) dt =[(t^2 /(−x+3i)) e^((−x+3i)t) ]_0 ^(+∞) −∫_0 ^∞ ((2t)/(−x+3i)) e^((−x+3i)t) dt =(2/(x−3i)) ∫_0 ^∞ t e^((−x+3i)t) dt =(2/(x−3i)){ [(t/(−x+3i)) e^((−x+3i)t) ]_0 ^(+∞) −∫_0 ^∞ (1/(−x+3i)) e^((−x+3i)t) dt} =(2/(x−3i))×(1/(x−3i)) ∫_0 ^∞ e^((−x+3i)t) dt =(2/((x−3i)^2 ))×[(1/(−x+3i)) e^((−x+3i)t) ]_0 ^(+∞) =(2/((x−3i)^3 )) =((2(x+3i)^3 )/((x^2 +9)^3 )) =((2(x^3 +3x^2 (3i)+3x(3i)^2 +(3i)^3 ))/((x^2 +9)^3 )) =((2(x^3 +9ix^2 −27x −27i))/((x^2 +9)^3 )) ⇒Im(...) =((2(9x^2 −27))/((x^2 +9)^3 )) e ⇒(x^2 +5x−3)L(y) =−1 +((18x^3 −54)/((x^2 +9)^3 )) ⇒ L(y) =−(1/(x^2 +5x−3)) +((18x^3 −54)/((x^2 +5x−3)(x^2 +9)^3 )) ⇒ y(x) =−L^(−1) ((1/(x^2 +5x −3)))+L^(−1) (((18x^3 −54)/((x^2 +5x−3)(x^2 +9)^3 )))...be continued....
$$\mathrm{let}\:\mathrm{take}\:\mathrm{a}\:\mathrm{try}\:\mathrm{with}\:\mathrm{laplace}\:\mathrm{transform} \\ $$$$\mathrm{e}\:\Rightarrow\mathrm{L}\left(\mathrm{y}^{''} \right)+\mathrm{5L}\left(\mathrm{y}^{'} \right)−\mathrm{3L}\left(\mathrm{y}\right)\:=\mathrm{L}\left(\mathrm{x}^{\mathrm{2}} \:\mathrm{sin}\left(\mathrm{3x}\right)\right)\:\Rightarrow \\ $$$$\mathrm{x}^{\mathrm{2}} \:\mathrm{L}\left(\mathrm{y}\right)−\mathrm{xy}\left(\mathrm{0}\right)−\mathrm{y}^{'} \left(\mathrm{0}\right)+\mathrm{5}\left(\mathrm{x}\:\mathrm{L}\left(\mathrm{y}\right)−\mathrm{y}\left(\mathrm{0}\right)\right)−\mathrm{3L}\left(\mathrm{y}\right)\:=\mathrm{L}\left(\mathrm{x}^{\mathrm{2}} \:\mathrm{sin}\left(\mathrm{3x}\right)\right)\:\Rightarrow \\ $$$$\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{5x}−\mathrm{3}\right)\mathrm{L}\left(\mathrm{y}\right)\:+\mathrm{1}\:=\mathrm{L}\left(\mathrm{x}^{\mathrm{2}} \:\mathrm{sin}\left(\mathrm{3x}\right)\:\mathrm{we}\:\mathrm{have}\:\right. \\ $$$$\mathrm{L}\left(\mathrm{x}^{\mathrm{2}} \:\mathrm{sin}\left(\mathrm{3x}\right)\right)\:=\int_{\mathrm{0}} ^{\infty} \:\mathrm{t}^{\mathrm{2}} \:\mathrm{sin}\left(\mathrm{3t}\right)\:\mathrm{e}^{−\mathrm{xt}} \:\mathrm{dt}\:=\mathrm{Im}\left(\int_{\mathrm{0}} ^{\infty} \:\mathrm{t}^{\mathrm{2}} \:\mathrm{e}^{\left(\mathrm{3i}−\mathrm{x}\right)\mathrm{t}} \:\mathrm{dt}\right) \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\mathrm{t}^{\mathrm{2}} \:\mathrm{e}^{\left(−\mathrm{x}+\mathrm{3i}\right)\mathrm{t}} \:\mathrm{dt}\:=\left[\frac{\mathrm{t}^{\mathrm{2}} }{−\mathrm{x}+\mathrm{3i}}\:\mathrm{e}^{\left(−\mathrm{x}+\mathrm{3i}\right)\mathrm{t}} \right]_{\mathrm{0}} ^{+\infty} \:−\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{2t}}{−\mathrm{x}+\mathrm{3i}}\:\mathrm{e}^{\left(−\mathrm{x}+\mathrm{3i}\right)\mathrm{t}} \:\mathrm{dt} \\ $$$$=\frac{\mathrm{2}}{\mathrm{x}−\mathrm{3i}}\:\int_{\mathrm{0}} ^{\infty} \:\:\mathrm{t}\:\mathrm{e}^{\left(−\mathrm{x}+\mathrm{3i}\right)\mathrm{t}} \:\mathrm{dt}\:=\frac{\mathrm{2}}{\mathrm{x}−\mathrm{3i}}\left\{\:\left[\frac{\mathrm{t}}{−\mathrm{x}+\mathrm{3i}}\:\mathrm{e}^{\left(−\mathrm{x}+\mathrm{3i}\right)\mathrm{t}} \right]_{\mathrm{0}} ^{+\infty} \:−\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{−\mathrm{x}+\mathrm{3i}}\:\mathrm{e}^{\left(−\mathrm{x}+\mathrm{3i}\right)\mathrm{t}} \:\mathrm{dt}\right\} \\ $$$$=\frac{\mathrm{2}}{\mathrm{x}−\mathrm{3i}}×\frac{\mathrm{1}}{\mathrm{x}−\mathrm{3i}}\:\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{\left(−\mathrm{x}+\mathrm{3i}\right)\mathrm{t}} \:\mathrm{dt}\:=\frac{\mathrm{2}}{\left(\mathrm{x}−\mathrm{3i}\right)^{\mathrm{2}} }×\left[\frac{\mathrm{1}}{−\mathrm{x}+\mathrm{3i}}\:\mathrm{e}^{\left(−\mathrm{x}+\mathrm{3i}\right)\mathrm{t}} \right]_{\mathrm{0}} ^{+\infty} \\ $$$$=\frac{\mathrm{2}}{\left(\mathrm{x}−\mathrm{3i}\right)^{\mathrm{3}} }\:=\frac{\mathrm{2}\left(\mathrm{x}+\mathrm{3i}\right)^{\mathrm{3}} }{\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{9}\right)^{\mathrm{3}} }\:=\frac{\mathrm{2}\left(\mathrm{x}^{\mathrm{3}} \:+\mathrm{3x}^{\mathrm{2}} \left(\mathrm{3i}\right)+\mathrm{3x}\left(\mathrm{3i}\right)^{\mathrm{2}} +\left(\mathrm{3i}\right)^{\mathrm{3}} \right)}{\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{9}\right)^{\mathrm{3}} } \\ $$$$=\frac{\mathrm{2}\left(\mathrm{x}^{\mathrm{3}} +\mathrm{9ix}^{\mathrm{2}} \:−\mathrm{27x}\:−\mathrm{27i}\right)}{\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{9}\right)^{\mathrm{3}} }\:\Rightarrow\mathrm{Im}\left(…\right)\:=\frac{\mathrm{2}\left(\mathrm{9x}^{\mathrm{2}} −\mathrm{27}\right)}{\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{9}\right)^{\mathrm{3}} } \\ $$$$\mathrm{e}\:\Rightarrow\left(\mathrm{x}^{\mathrm{2}} +\mathrm{5x}−\mathrm{3}\right)\mathrm{L}\left(\mathrm{y}\right)\:=−\mathrm{1}\:+\frac{\mathrm{18x}^{\mathrm{3}} −\mathrm{54}}{\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{9}\right)^{\mathrm{3}} }\:\Rightarrow \\ $$$$\mathrm{L}\left(\mathrm{y}\right)\:=−\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{5x}−\mathrm{3}}\:+\frac{\mathrm{18x}^{\mathrm{3}} \:−\mathrm{54}}{\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{5x}−\mathrm{3}\right)\left(\mathrm{x}^{\mathrm{2}} +\mathrm{9}\right)^{\mathrm{3}} }\:\Rightarrow \\ $$$$\mathrm{y}\left(\mathrm{x}\right)\:=−\mathrm{L}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{5x}\:−\mathrm{3}}\right)+\mathrm{L}^{−\mathrm{1}} \left(\frac{\mathrm{18x}^{\mathrm{3}} \:−\mathrm{54}}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{5x}−\mathrm{3}\right)\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{9}\right)^{\mathrm{3}} }\right)…\mathrm{be}\:\mathrm{continued}…. \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *