Menu Close

solve-y-y-1-cosx-

Tinku Tara 0 Comments
Pin




Question Number 97794 by abdomathmax last updated on 09/Jun/20
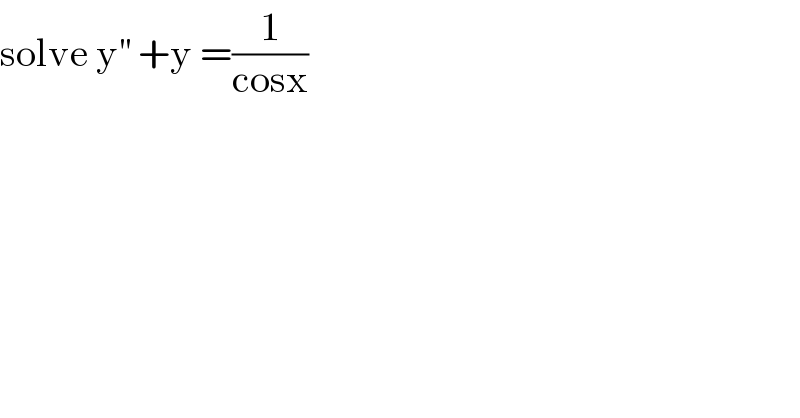
solve y^(′′) +y =(1/(cosx))
$$\mathrm{solve}\:\mathrm{y}^{''} \:+\mathrm{y}\:=\frac{\mathrm{1}}{\mathrm{cosx}} \\ $$
Commented by john santu last updated on 10/Jun/20
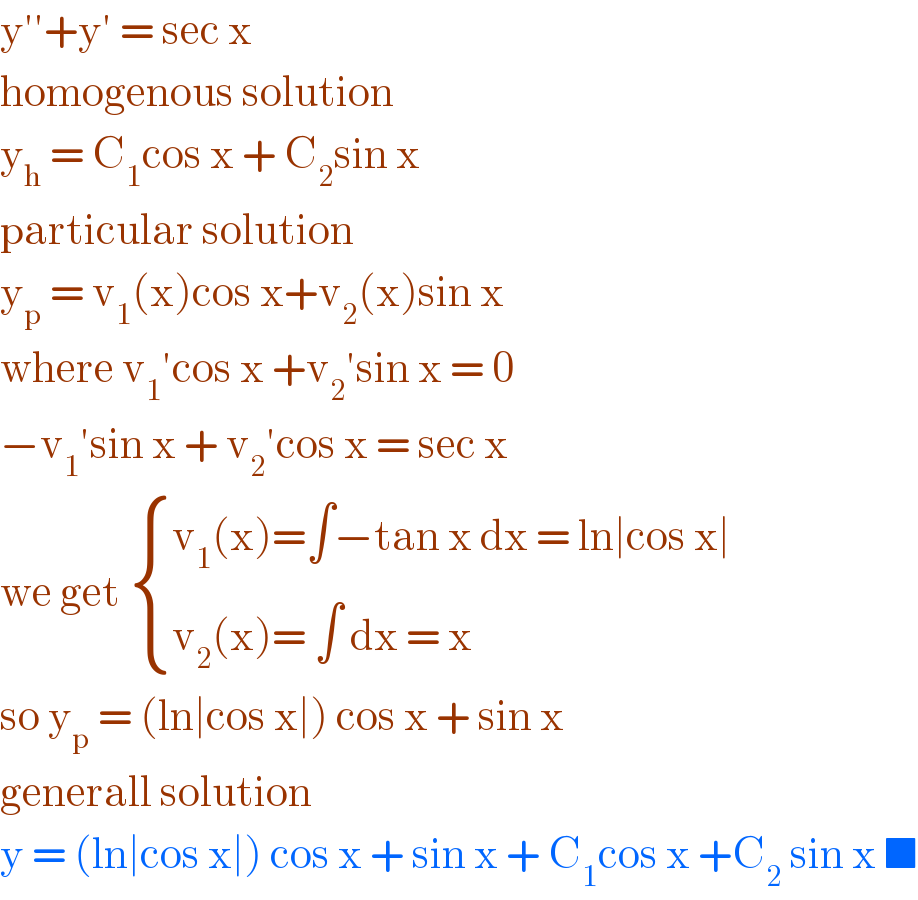
y′′+y′ = sec x homogenous solution y_h = C_1 cos x + C_2 sin x particular solution y_p = v_1 (x)cos x+v_2 (x)sin x where v_1 ′cos x +v_2 ′sin x = 0 −v_1 ′sin x + v_2 ′cos x = sec x we get { ((v_1 (x)=∫−tan x dx = ln∣cos x∣)),((v_2 (x)= ∫ dx = x)) :} so y_p = (ln∣cos x∣) cos x + sin x generall solution y = (ln∣cos x∣) cos x + sin x + C_1 cos x +C_2 sin x ■
$$\mathrm{y}''+\mathrm{y}'\:=\:\mathrm{sec}\:\mathrm{x} \\ $$$$\mathrm{homogenous}\:\mathrm{solution}\: \\ $$$$\mathrm{y}_{\mathrm{h}} \:=\:\mathrm{C}_{\mathrm{1}} \mathrm{cos}\:\mathrm{x}\:+\:\mathrm{C}_{\mathrm{2}} \mathrm{sin}\:\mathrm{x}\: \\ $$$$\mathrm{particular}\:\mathrm{solution}\: \\ $$$$\mathrm{y}_{\mathrm{p}} \:=\:\mathrm{v}_{\mathrm{1}} \left(\mathrm{x}\right)\mathrm{cos}\:\mathrm{x}+\mathrm{v}_{\mathrm{2}} \left(\mathrm{x}\right)\mathrm{sin}\:\mathrm{x} \\ $$$$\mathrm{where}\:\mathrm{v}_{\mathrm{1}} '\mathrm{cos}\:\mathrm{x}\:+\mathrm{v}_{\mathrm{2}} '\mathrm{sin}\:\mathrm{x}\:=\:\mathrm{0} \\ $$$$−\mathrm{v}_{\mathrm{1}} '\mathrm{sin}\:\mathrm{x}\:+\:\mathrm{v}_{\mathrm{2}} '\mathrm{cos}\:\mathrm{x}\:=\:\mathrm{sec}\:\mathrm{x} \\ $$$$\mathrm{we}\:\mathrm{get}\:\begin{cases}{\mathrm{v}_{\mathrm{1}} \left(\mathrm{x}\right)=\int−\mathrm{tan}\:\mathrm{x}\:\mathrm{dx}\:=\:\mathrm{ln}\mid\mathrm{cos}\:\mathrm{x}\mid}\\{\mathrm{v}_{\mathrm{2}} \left(\mathrm{x}\right)=\:\int\:\mathrm{dx}\:=\:\mathrm{x}}\end{cases} \\ $$$$\mathrm{so}\:\mathrm{y}_{\mathrm{p}} \:=\:\left(\mathrm{ln}\mid\mathrm{cos}\:\mathrm{x}\mid\right)\:\mathrm{cos}\:\mathrm{x}\:+\:\mathrm{sin}\:\mathrm{x} \\ $$$$\mathrm{generall}\:\mathrm{solution}\: \\ $$$$\mathrm{y}\:=\:\left(\mathrm{ln}\mid\mathrm{cos}\:\mathrm{x}\mid\right)\:\mathrm{cos}\:\mathrm{x}\:+\:\mathrm{sin}\:\mathrm{x}\:+\:\mathrm{C}_{\mathrm{1}} \mathrm{cos}\:\mathrm{x}\:+\mathrm{C}_{\mathrm{2}} \:\mathrm{sin}\:\mathrm{x}\:\blacksquare \\ $$
Commented by bobhans last updated on 10/Jun/20
nice.....very...nice
Commented by bemath last updated on 10/Jun/20
very....afdolll
Answered by niroj last updated on 09/Jun/20
y^(′′) +y = (1/(cos x)) (d^2 y/dx^2 )+y = (1/(cos x)) (D^2 +1)y= sec x A.E. , m^2 +1=0 m= 0+^− 1i CF= C_1 cos x+C_2 sin x Here, By the help of variation parameters: y_1 = cos x, y_2 = sin x , w= sec x W= determinant (((y_1 y_2 )),((y_1 ^′ y_2 ^′ ))) W= determinant ((( cos x sin x)),((−sin x cos x))) W = cos^2 x−(−sin^2 x)= 1 W=1 PI= −y_1 ∫ ((y_2 x)/w)dx +y_2 ∫((y_1 x)/w)dx =−cosx∫(( sin x sec x)/1)dx +sin x∫ ((cos x sec x)/1)dx = −cos x∫tan x dx +sinx ∫dx = −cos x log (sec x)+sin x .x y=CF+PI ∴ y= C_1 cos x+C_2 sin x −cos x log (sec x)+x sin xo
$$\:\:\mathrm{y}^{''} +\mathrm{y}\:=\:\frac{\mathrm{1}}{\mathrm{cos}\:\mathrm{x}} \\ $$$$\:\:\frac{\mathrm{d}^{\mathrm{2}} \mathrm{y}}{\mathrm{dx}^{\mathrm{2}} }+\mathrm{y}\:=\:\frac{\mathrm{1}}{\mathrm{cos}\:\mathrm{x}} \\ $$$$\:\:\:\left(\mathrm{D}^{\mathrm{2}} +\mathrm{1}\right)\mathrm{y}=\:\mathrm{sec}\:\mathrm{x} \\ $$$$\:\:\mathrm{A}.\mathrm{E}.\:,\:\:\mathrm{m}^{\mathrm{2}} +\mathrm{1}=\mathrm{0} \\ $$$$\:\:\:\:\mathrm{m}=\:\mathrm{0}\overset{−} {+}\mathrm{1i} \\ $$$$\:\mathrm{CF}=\:\mathrm{C}_{\mathrm{1}} \mathrm{cos}\:\mathrm{x}+\mathrm{C}_{\mathrm{2}} \mathrm{sin}\:\mathrm{x} \\ $$$$\:\mathrm{Here},\:\mathrm{By}\:\mathrm{the}\:\mathrm{help}\:\mathrm{of}\:\mathrm{variation}\:\mathrm{parameters}: \\ $$$$\:\:\mathrm{y}_{\mathrm{1}} =\:\mathrm{cos}\:\mathrm{x},\:\:\mathrm{y}_{\mathrm{2}} =\:\mathrm{sin}\:\mathrm{x}\:,\:\mathrm{w}=\:\mathrm{sec}\:\mathrm{x} \\ $$$$\:\:\:\mathrm{W}=\:\begin{vmatrix}{\mathrm{y}_{\mathrm{1}} \:\:\:\mathrm{y}_{\mathrm{2}} }\\{\mathrm{y}_{\mathrm{1}} ^{'} \:\:\:\mathrm{y}_{\mathrm{2}} ^{'} }\end{vmatrix} \\ $$$$\:\:\:\:\mathrm{W}=\:\begin{vmatrix}{\:\mathrm{cos}\:\mathrm{x}\:\:\:\:\:\:\:\mathrm{sin}\:\mathrm{x}}\\{−\mathrm{sin}\:\mathrm{x}\:\:\:\:\:\mathrm{cos}\:\mathrm{x}}\end{vmatrix} \\ $$$$\:\:\:\mathrm{W}\:=\:\mathrm{cos}^{\mathrm{2}} \mathrm{x}−\left(−\mathrm{sin}^{\mathrm{2}} \mathrm{x}\right)=\:\mathrm{1} \\ $$$$\:\:\:\:\mathrm{W}=\mathrm{1} \\ $$$$\:\mathrm{PI}=\:−\mathrm{y}_{\mathrm{1}} \int\:\frac{\mathrm{y}_{\mathrm{2}} \:\mathrm{x}}{\mathrm{w}}\mathrm{dx}\:+\mathrm{y}_{\mathrm{2}} \int\frac{\mathrm{y}_{\mathrm{1}} \mathrm{x}}{\mathrm{w}}\mathrm{dx} \\ $$$$\:\:=−\mathrm{cosx}\int\frac{\:\mathrm{sin}\:\mathrm{x}\:\mathrm{sec}\:\mathrm{x}}{\mathrm{1}}\mathrm{dx}\:+\mathrm{sin}\:\mathrm{x}\int\:\frac{\mathrm{cos}\:\mathrm{x}\:\mathrm{sec}\:\mathrm{x}}{\mathrm{1}}\mathrm{dx} \\ $$$$\:\:=\:−\mathrm{cos}\:\mathrm{x}\int\mathrm{tan}\:\mathrm{x}\:\mathrm{dx}\:+\mathrm{sinx}\:\int\mathrm{dx} \\ $$$$\:\:=\:−\mathrm{cos}\:\mathrm{x}\:\mathrm{log}\:\left(\mathrm{sec}\:\mathrm{x}\right)+\mathrm{sin}\:\mathrm{x}\:.\mathrm{x}\: \\ $$$$\:\:\mathrm{y}=\mathrm{CF}+\mathrm{PI} \\ $$$$\:\therefore\:\mathrm{y}=\:\mathrm{C}_{\mathrm{1}} \mathrm{cos}\:\mathrm{x}+\mathrm{C}_{\mathrm{2}} \mathrm{sin}\:\mathrm{x}\:−\mathrm{cos}\:\mathrm{x}\:\mathrm{log}\:\left(\mathrm{sec}\:\mathrm{x}\right)+\mathrm{x}\:\mathrm{sin}\:\mathrm{xo} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *