Question Number 90972 by abdomathmax last updated on 27/Apr/20
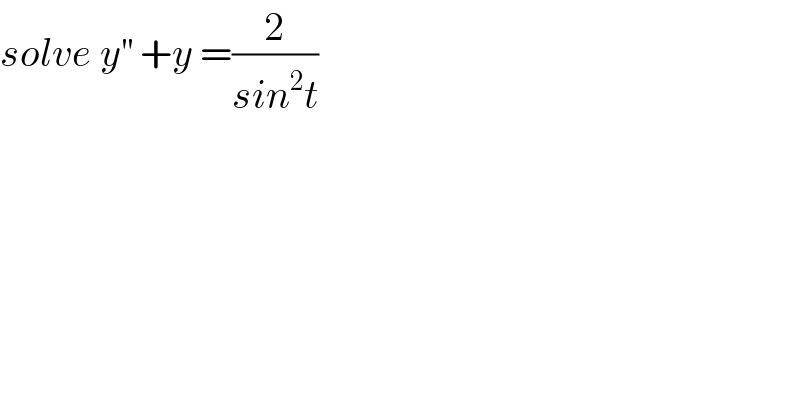
$${solve}\:{y}^{''} \:+{y}\:=\frac{\mathrm{2}}{{sin}^{\mathrm{2}} {t}} \\ $$
Answered by Joel578 last updated on 27/Apr/20

$$\bullet\:\mathrm{Homogeneous}\:\mathrm{solution} \\ $$$$\mathrm{with}\:\mathrm{char}.\:\mathrm{eq}.\:\lambda^{\mathrm{2}} \:+\:\mathrm{1}\:=\:\mathrm{0}\:\rightarrow\:\lambda_{\mathrm{1},\mathrm{2}} \:=\:\pm\:{i} \\ $$$$\Rightarrow\:{y}_{{h}} \left({t}\right)\:=\:{c}_{\mathrm{1}} \mathrm{cos}\:{t}\:+\:{c}_{\mathrm{2}} \:\mathrm{sin}\:{t} \\ $$$$ \\ $$$$\bullet\:\mathrm{Particular}\:\mathrm{soution}\:\mathrm{for}\:{r}\left({t}\right)\:=\:\frac{\mathrm{2}}{\mathrm{sin}^{\mathrm{2}} \:{t}}\: \\ $$$$\mathrm{using}\:\mathrm{variation}\:\mathrm{of}\:\mathrm{parameter}\:\mathrm{method} \\ $$$$\mathrm{Let}\:{y}_{\mathrm{1}} \left({t}\right)\:=\:\mathrm{cos}\:{t}\:\:\mathrm{and}\:\:{y}_{\mathrm{2}} \left({t}\right)\:=\:\mathrm{sin}\:{t} \\ $$$$\mathrm{The}\:\mathrm{particular}\:\mathrm{solution}\:\mathrm{will}\:\mathrm{be}\:\mathrm{in}\:\mathrm{form} \\ $$$${y}_{{p}} \left({t}\right)\:=\:{u}\left({t}\right){y}_{\mathrm{1}} \left({t}\right)\:+\:{v}\left({t}\right){y}_{\mathrm{2}} \left({t}\right) \\ $$$$\mathrm{where} \\ $$$${u}\left({t}\right)\:=\:−\int\:\:\frac{{r}\left({t}\right)\:{y}_{\mathrm{2}} \left({t}\right)}{{W}\left({t}\right)}\:{dt}\:\:\mathrm{and}\:{v}\left({t}\right)\:=\:\int\:\frac{{r}\left({t}\right)\:{y}_{\mathrm{1}} \left({t}\right)}{{W}\left({t}\right)}\:{dt} \\ $$$$\mathrm{Now},\: \\ $$$${W}\left({t}\right)\:=\:\begin{vmatrix}{{y}_{\mathrm{1}} }&{{y}_{\mathrm{2}} }\\{{y}_{\mathrm{1}} '}&{{y}_{\mathrm{2}} '}\end{vmatrix}=\:\begin{vmatrix}{\:\:\:\mathrm{cos}\:{t}}&{\mathrm{sin}\:{t}}\\{−\mathrm{sin}\:{t}}&{\mathrm{cos}\:{t}}\end{vmatrix}=\:\mathrm{1} \\ $$$$\mathrm{therefore}\: \\ $$$${u}\left({t}\right)\:=\:−\int\:\frac{\mathrm{2}}{\mathrm{sin}^{\mathrm{2}} \:{t}}\:.\:\mathrm{sin}\:{t}\:{dt}\:=\:\mathrm{2}\:\mathrm{ln}\:\left(\mathrm{csc}\:{x}\:+\:\mathrm{cot}\:{x}\right) \\ $$$${v}\left({t}\right)\:=\:\int\:\frac{\mathrm{2}}{\mathrm{sin}^{\mathrm{2}} \:{t}}\:.\:\mathrm{cos}\:{t}\:{dt}\:=\:−\frac{\mathrm{2}}{\mathrm{sin}\:{t}} \\ $$$$\Rightarrow\:{y}_{{p}} \left({t}\right)\:=\:\mathrm{2}\left(\mathrm{cos}\:{t}\right)\mathrm{ln}\:\left(\mathrm{csc}\:{x}\:+\:\mathrm{cot}\:{x}\right)\:−\:\mathrm{2} \\ $$$$ \\ $$$$\therefore\:{y}\left({t}\right)\:=\:{c}_{\mathrm{1}} \mathrm{cos}\:{t}\:+\:{c}_{\mathrm{2}} \:\mathrm{sin}\:{t}\:+\:\mathrm{2}\left(\mathrm{cos}\:{t}\right)\mathrm{ln}\:\left(\mathrm{csc}\:{x}\:+\:\mathrm{cot}\:{x}\right)\:−\:\mathrm{2} \\ $$
Commented by mathmax by abdo last updated on 28/Apr/20

$${thank}\:{you}\:{sir}. \\ $$
