Question Number 96773 by abdomathmax last updated on 04/Jun/20
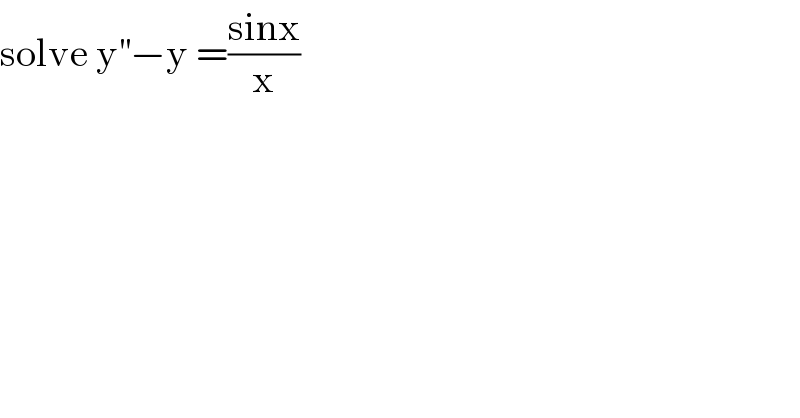
$$\mathrm{solve}\:\mathrm{y}^{''} −\mathrm{y}\:=\frac{\mathrm{sinx}}{\mathrm{x}} \\ $$
Answered by abdomathmax last updated on 05/Jun/20
![let solve by laplace (e)⇒L(y^(′′) )−L(y) =L(((sinx)/x)) ⇒ x^2 L(y)−xy(0)−y^′ (0) −L(y) =L(((sinx)/x)) ⇒ (x^2 −1)L(y) =xy(0)+y^′ (0)+L(((sinx)/x)) we have L(((sinx)/x)) =∫_0 ^∞ ((sint)/t) e^(−xt) dt =f(x) f^′ (x) =−∫_0 ^∞ sint e^(−xt) dt =−Im(∫_0 ^∞ e^(it−xt) dt) ∫_0 ^∞ e^((−x+i)t) dt =[(1/(−x+i)) e^((−x+i)t) ]_0 ^∞ =−(1/(−x+i)) =(1/(x−i)) =((x+i)/(x^2 +1)) ⇒f^′ (x) =−(1/(1+x^2 )) ⇒ f(x)=−arrctanx +c f(0) =(π/2) =0+c ⇒f(x) =(π/2) −arcrtanx e ⇒(x^2 −1)L(y) =xy(0)+y^′ (0)+(π/2)−arctanx ⇒L(y) =y(0)(x/(x^2 −1)) +((y^′ (0)+(π/2))/(x^2 −1))−((arctanx)/(x^2 −1)) y(x) =y(0)L^(−1) ((x/(x^2 −1)))+(y^′ (0)+(π/2))L^(−1) ((1/(x^2 −1))) −L^(−1) (((arctanx)/(x^2 −1))) (x/(x^2 −1)) =(x/((x−1)(x+1))) =(a/(x−1)) +(b/(x+1)) ⇒ a =(1/2) and b =(1/2) ⇒L^(−1) ((x/(x^2 −1))) =(1/2)e^x +(1/2)e^(−x) =ch(x) (1/(x^2 −1)) =(1/2)((1/(x−1))−(1/(x+1))) ⇒ L^(−1) ((1/(x^2 −1))) =(e^x /2)−(e^(−x) /2) =sh(x) rest to find L^(−1) (((arctanx)/(x^2 −1)))=δ(x) ⇒ y(x) =y(o)ch(x)+(y^′ (0)+(π/2))shx +δ(x)](https://www.tinkutara.com/question/Q96934.png)
$$\mathrm{let}\:\mathrm{solve}\:\mathrm{by}\:\mathrm{laplace}\: \\ $$$$\left(\mathrm{e}\right)\Rightarrow\mathrm{L}\left(\mathrm{y}^{''} \right)−\mathrm{L}\left(\mathrm{y}\right)\:=\mathrm{L}\left(\frac{\mathrm{sinx}}{\mathrm{x}}\right)\:\Rightarrow \\ $$$$\mathrm{x}^{\mathrm{2}} \mathrm{L}\left(\mathrm{y}\right)−\mathrm{xy}\left(\mathrm{0}\right)−\mathrm{y}^{'} \left(\mathrm{0}\right)\:−\mathrm{L}\left(\mathrm{y}\right)\:=\mathrm{L}\left(\frac{\mathrm{sinx}}{\mathrm{x}}\right)\:\Rightarrow \\ $$$$\left(\mathrm{x}^{\mathrm{2}} −\mathrm{1}\right)\mathrm{L}\left(\mathrm{y}\right)\:=\mathrm{xy}\left(\mathrm{0}\right)+\mathrm{y}^{'} \left(\mathrm{0}\right)+\mathrm{L}\left(\frac{\mathrm{sinx}}{\mathrm{x}}\right) \\ $$$$\mathrm{we}\:\mathrm{have}\:\mathrm{L}\left(\frac{\mathrm{sinx}}{\mathrm{x}}\right)\:=\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{sint}}{\mathrm{t}}\:\mathrm{e}^{−\mathrm{xt}} \:\mathrm{dt}\:=\mathrm{f}\left(\mathrm{x}\right) \\ $$$$\mathrm{f}^{'} \left(\mathrm{x}\right)\:=−\int_{\mathrm{0}} ^{\infty} \:\mathrm{sint}\:\mathrm{e}^{−\mathrm{xt}} \:\mathrm{dt}\:=−\mathrm{Im}\left(\int_{\mathrm{0}} ^{\infty} \mathrm{e}^{\mathrm{it}−\mathrm{xt}} \mathrm{dt}\right) \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{\left(−\mathrm{x}+\mathrm{i}\right)\mathrm{t}} \:\mathrm{dt}\:=\left[\frac{\mathrm{1}}{−\mathrm{x}+\mathrm{i}}\:\mathrm{e}^{\left(−\mathrm{x}+\mathrm{i}\right)\mathrm{t}} \right]_{\mathrm{0}} ^{\infty} \\ $$$$=−\frac{\mathrm{1}}{−\mathrm{x}+\mathrm{i}}\:=\frac{\mathrm{1}}{\mathrm{x}−\mathrm{i}}\:=\frac{\mathrm{x}+\mathrm{i}}{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}\:\Rightarrow\mathrm{f}^{'} \left(\mathrm{x}\right)\:=−\frac{\mathrm{1}}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\:\Rightarrow \\ $$$$\mathrm{f}\left(\mathrm{x}\right)=−\mathrm{arrctanx}\:+\mathrm{c} \\ $$$$\mathrm{f}\left(\mathrm{0}\right)\:=\frac{\pi}{\mathrm{2}}\:=\mathrm{0}+\mathrm{c}\:\Rightarrow\mathrm{f}\left(\mathrm{x}\right)\:=\frac{\pi}{\mathrm{2}}\:−\mathrm{arcrtanx} \\ $$$$\mathrm{e}\:\Rightarrow\left(\mathrm{x}^{\mathrm{2}} −\mathrm{1}\right)\mathrm{L}\left(\mathrm{y}\right)\:=\mathrm{xy}\left(\mathrm{0}\right)+\mathrm{y}^{'} \left(\mathrm{0}\right)+\frac{\pi}{\mathrm{2}}−\mathrm{arctanx} \\ $$$$\Rightarrow\mathrm{L}\left(\mathrm{y}\right)\:=\mathrm{y}\left(\mathrm{0}\right)\frac{\mathrm{x}}{\mathrm{x}^{\mathrm{2}} −\mathrm{1}}\:+\frac{\mathrm{y}^{'} \left(\mathrm{0}\right)+\frac{\pi}{\mathrm{2}}}{\mathrm{x}^{\mathrm{2}} −\mathrm{1}}−\frac{\mathrm{arctanx}}{\mathrm{x}^{\mathrm{2}} −\mathrm{1}} \\ $$$$\mathrm{y}\left(\mathrm{x}\right)\:=\mathrm{y}\left(\mathrm{0}\right)\mathrm{L}^{−\mathrm{1}} \left(\frac{\mathrm{x}}{\mathrm{x}^{\mathrm{2}} −\mathrm{1}}\right)+\left(\mathrm{y}^{'} \left(\mathrm{0}\right)+\frac{\pi}{\mathrm{2}}\right)\mathrm{L}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} −\mathrm{1}}\right) \\ $$$$−\mathrm{L}^{−\mathrm{1}} \left(\frac{\mathrm{arctanx}}{\mathrm{x}^{\mathrm{2}} −\mathrm{1}}\right) \\ $$$$\frac{\mathrm{x}}{\mathrm{x}^{\mathrm{2}} −\mathrm{1}}\:=\frac{\mathrm{x}}{\left(\mathrm{x}−\mathrm{1}\right)\left(\mathrm{x}+\mathrm{1}\right)}\:=\frac{\mathrm{a}}{\mathrm{x}−\mathrm{1}}\:+\frac{\mathrm{b}}{\mathrm{x}+\mathrm{1}}\:\Rightarrow \\ $$$$\mathrm{a}\:=\frac{\mathrm{1}}{\mathrm{2}}\:\mathrm{and}\:\mathrm{b}\:=\frac{\mathrm{1}}{\mathrm{2}}\:\Rightarrow\mathrm{L}^{−\mathrm{1}} \left(\frac{\mathrm{x}}{\mathrm{x}^{\mathrm{2}} −\mathrm{1}}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{e}^{\mathrm{x}} \:+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{e}^{−\mathrm{x}} \:=\mathrm{ch}\left(\mathrm{x}\right) \\ $$$$\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} −\mathrm{1}}\:=\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}}{\mathrm{x}−\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{x}+\mathrm{1}}\right)\:\Rightarrow \\ $$$$\mathrm{L}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} −\mathrm{1}}\right)\:=\frac{\mathrm{e}^{\mathrm{x}} }{\mathrm{2}}−\frac{\mathrm{e}^{−\mathrm{x}} }{\mathrm{2}}\:=\mathrm{sh}\left(\mathrm{x}\right)\:\mathrm{rest}\:\mathrm{to}\:\mathrm{find} \\ $$$$\mathrm{L}^{−\mathrm{1}} \left(\frac{\mathrm{arctanx}}{\mathrm{x}^{\mathrm{2}} −\mathrm{1}}\right)=\delta\left(\mathrm{x}\right)\:\Rightarrow \\ $$$$\mathrm{y}\left(\mathrm{x}\right)\:=\mathrm{y}\left(\mathrm{o}\right)\mathrm{ch}\left(\mathrm{x}\right)+\left(\mathrm{y}^{'} \left(\mathrm{0}\right)+\frac{\pi}{\mathrm{2}}\right)\mathrm{shx}\:+\delta\left(\mathrm{x}\right) \\ $$$$ \\ $$
