Menu Close

solve-y-y-y-4-at-y-0-1-

Tinku Tara 0 Comments
Pin




Question Number 103767 by bramlex last updated on 17/Jul/20
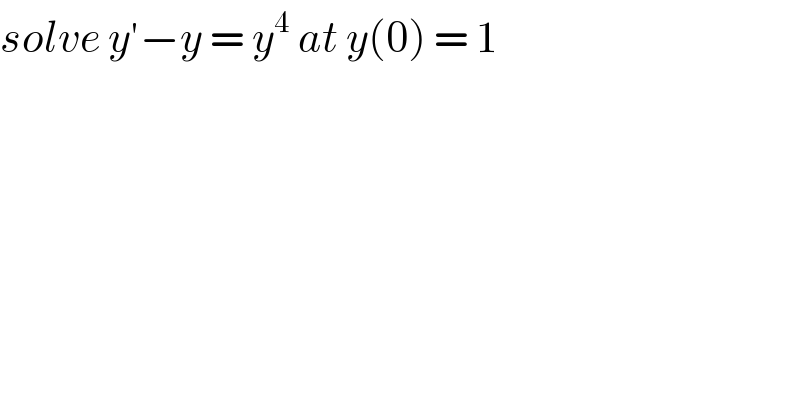
solve y′−y = y^4 at y(0) = 1
$${solve}\:{y}'−{y}\:=\:{y}^{\mathrm{4}} \:{at}\:{y}\left(\mathrm{0}\right)\:=\:\mathrm{1}\: \\ $$
Answered by bemath last updated on 17/Jul/20
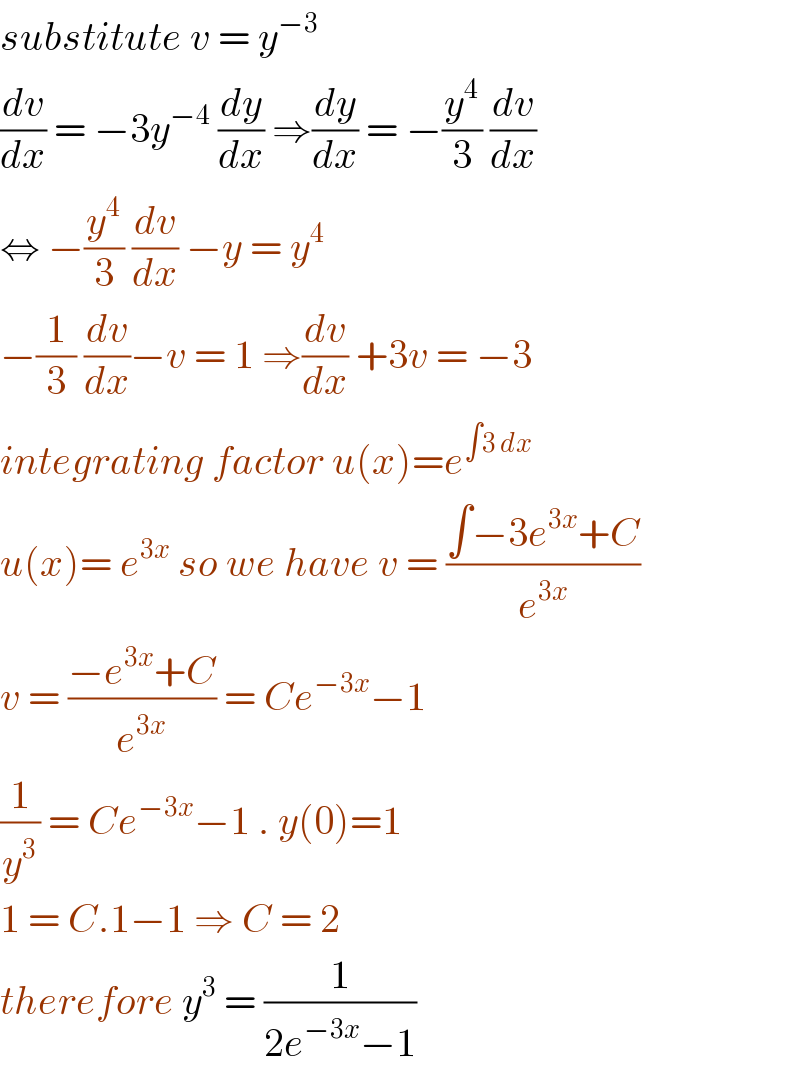
substitute v = y^(−3) (dv/dx) = −3y^(−4) (dy/dx) ⇒(dy/dx) = −(y^4 /3) (dv/dx) ⇔ −(y^4 /3) (dv/dx) −y = y^4 −(1/3) (dv/dx)−v = 1 ⇒(dv/dx) +3v = −3 integrating factor u(x)=e^(∫3 dx) u(x)= e^(3x) so we have v = ((∫−3e^(3x) +C)/e^(3x) ) v = ((−e^(3x) +C)/e^(3x) ) = Ce^(−3x) −1 (1/y^3 ) = Ce^(−3x) −1 . y(0)=1 1 = C.1−1 ⇒ C = 2 therefore y^3 = (1/(2e^(−3x) −1))
$${substitute}\:{v}\:=\:{y}^{−\mathrm{3}} \\ $$$$\frac{{dv}}{{dx}}\:=\:−\mathrm{3}{y}^{−\mathrm{4}} \:\frac{{dy}}{{dx}}\:\Rightarrow\frac{{dy}}{{dx}}\:=\:−\frac{{y}^{\mathrm{4}} }{\mathrm{3}}\:\frac{{dv}}{{dx}} \\ $$$$\Leftrightarrow\:−\frac{{y}^{\mathrm{4}} }{\mathrm{3}}\:\frac{{dv}}{{dx}}\:−{y}\:=\:{y}^{\mathrm{4}} \\ $$$$−\frac{\mathrm{1}}{\mathrm{3}}\:\frac{{dv}}{{dx}}−{v}\:=\:\mathrm{1}\:\Rightarrow\frac{{dv}}{{dx}}\:+\mathrm{3}{v}\:=\:−\mathrm{3} \\ $$$${integrating}\:{factor}\:{u}\left({x}\right)={e}^{\int\mathrm{3}\:{dx}} \\ $$$${u}\left({x}\right)=\:{e}^{\mathrm{3}{x}} \:{so}\:{we}\:{have}\:{v}\:=\:\frac{\int−\mathrm{3}{e}^{\mathrm{3}{x}} +{C}}{{e}^{\mathrm{3}{x}} } \\ $$$${v}\:=\:\frac{−{e}^{\mathrm{3}{x}} +{C}}{{e}^{\mathrm{3}{x}} }\:=\:{Ce}^{−\mathrm{3}{x}} −\mathrm{1} \\ $$$$\frac{\mathrm{1}}{{y}^{\mathrm{3}} }\:=\:{Ce}^{−\mathrm{3}{x}} −\mathrm{1}\:.\:{y}\left(\mathrm{0}\right)=\mathrm{1} \\ $$$$\mathrm{1}\:=\:{C}.\mathrm{1}−\mathrm{1}\:\Rightarrow\:{C}\:=\:\mathrm{2}\: \\ $$$${therefore}\:{y}^{\mathrm{3}} \:=\:\frac{\mathrm{1}}{\mathrm{2}{e}^{−\mathrm{3}{x}} −\mathrm{1}} \\ $$
Answered by mathmax by abdo last updated on 18/Jul/20
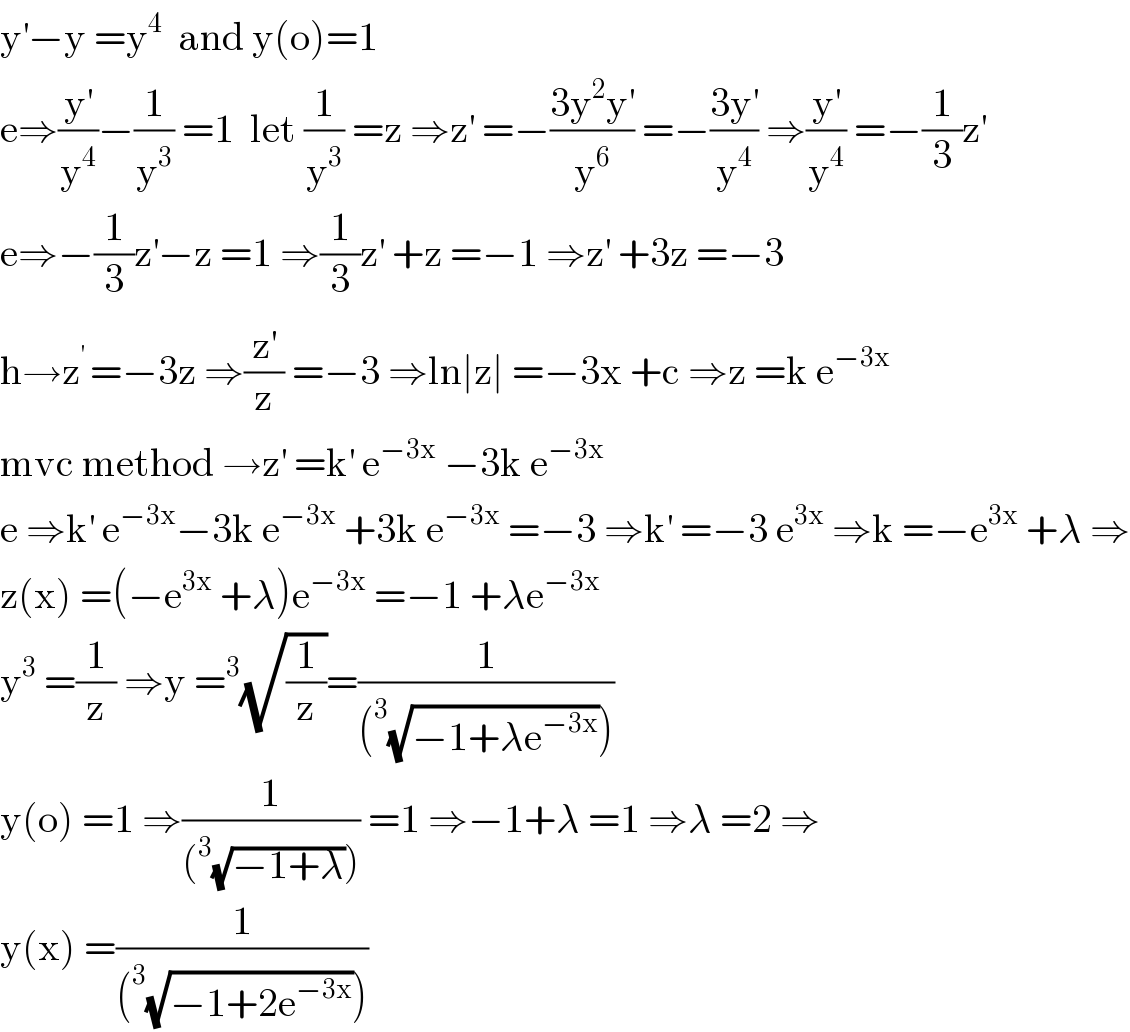
y^′ −y =y^4 and y(o)=1 e⇒(y^′ /y^4 )−(1/y^3 ) =1 let (1/y^3 ) =z ⇒z^′ =−((3y^2 y^′ )/y^6 ) =−((3y^′ )/y^4 ) ⇒(y^′ /y^4 ) =−(1/3)z^′ e⇒−(1/3)z^′ −z =1 ⇒(1/3)z^′ +z =−1 ⇒z^′ +3z =−3 h→z^(′ ) =−3z ⇒(z^′ /z) =−3 ⇒ln∣z∣ =−3x +c ⇒z =k e^(−3x) mvc method →z^′ =k^′ e^(−3x) −3k e^(−3x) e ⇒k^′ e^(−3x) −3k e^(−3x) +3k e^(−3x) =−3 ⇒k^′ =−3 e^(3x) ⇒k =−e^(3x) +λ ⇒ z(x) =(−e^(3x) +λ)e^(−3x) =−1 +λe^(−3x) y^3 =(1/z) ⇒y =^3 (√(1/z))=(1/((^3 (√(−1+λe^(−3x) ))))) y(o) =1 ⇒(1/((^3 (√(−1+λ))))) =1 ⇒−1+λ =1 ⇒λ =2 ⇒ y(x) =(1/((^3 (√(−1+2e^(−3x) )))))
$$\mathrm{y}^{'} −\mathrm{y}\:=\mathrm{y}^{\mathrm{4}} \:\:\mathrm{and}\:\mathrm{y}\left(\mathrm{o}\right)=\mathrm{1} \\ $$$$\mathrm{e}\Rightarrow\frac{\mathrm{y}^{'} }{\mathrm{y}^{\mathrm{4}} }−\frac{\mathrm{1}}{\mathrm{y}^{\mathrm{3}} }\:=\mathrm{1}\:\:\mathrm{let}\:\frac{\mathrm{1}}{\mathrm{y}^{\mathrm{3}} }\:=\mathrm{z}\:\Rightarrow\mathrm{z}^{'} \:=−\frac{\mathrm{3y}^{\mathrm{2}} \mathrm{y}^{'} }{\mathrm{y}^{\mathrm{6}} }\:=−\frac{\mathrm{3y}^{'} }{\mathrm{y}^{\mathrm{4}} }\:\Rightarrow\frac{\mathrm{y}^{'} }{\mathrm{y}^{\mathrm{4}} }\:=−\frac{\mathrm{1}}{\mathrm{3}}\mathrm{z}^{'} \\ $$$$\mathrm{e}\Rightarrow−\frac{\mathrm{1}}{\mathrm{3}}\mathrm{z}^{'} −\mathrm{z}\:=\mathrm{1}\:\Rightarrow\frac{\mathrm{1}}{\mathrm{3}}\mathrm{z}^{'} \:+\mathrm{z}\:=−\mathrm{1}\:\Rightarrow\mathrm{z}^{'} \:+\mathrm{3z}\:=−\mathrm{3} \\ $$$$\mathrm{h}\rightarrow\mathrm{z}^{'\:} =−\mathrm{3z}\:\Rightarrow\frac{\mathrm{z}^{'} }{\mathrm{z}}\:=−\mathrm{3}\:\Rightarrow\mathrm{ln}\mid\mathrm{z}\mid\:=−\mathrm{3x}\:+\mathrm{c}\:\Rightarrow\mathrm{z}\:=\mathrm{k}\:\mathrm{e}^{−\mathrm{3x}} \\ $$$$\mathrm{mvc}\:\mathrm{method}\:\rightarrow\mathrm{z}^{'} \:=\mathrm{k}^{'} \:\mathrm{e}^{−\mathrm{3x}} \:−\mathrm{3k}\:\mathrm{e}^{−\mathrm{3x}} \\ $$$$\mathrm{e}\:\Rightarrow\mathrm{k}^{'} \:\mathrm{e}^{−\mathrm{3x}} −\mathrm{3k}\:\mathrm{e}^{−\mathrm{3x}} \:+\mathrm{3k}\:\mathrm{e}^{−\mathrm{3x}} \:=−\mathrm{3}\:\Rightarrow\mathrm{k}^{'} \:=−\mathrm{3}\:\mathrm{e}^{\mathrm{3x}} \:\Rightarrow\mathrm{k}\:=−\mathrm{e}^{\mathrm{3x}} \:+\lambda\:\Rightarrow \\ $$$$\mathrm{z}\left(\mathrm{x}\right)\:=\left(−\mathrm{e}^{\mathrm{3x}} \:+\lambda\right)\mathrm{e}^{−\mathrm{3x}} \:=−\mathrm{1}\:+\lambda\mathrm{e}^{−\mathrm{3x}} \\ $$$$\mathrm{y}^{\mathrm{3}} \:=\frac{\mathrm{1}}{\mathrm{z}}\:\Rightarrow\mathrm{y}\:=^{\mathrm{3}} \sqrt{\frac{\mathrm{1}}{\mathrm{z}}}=\frac{\mathrm{1}}{\left(^{\mathrm{3}} \sqrt{−\mathrm{1}+\lambda\mathrm{e}^{−\mathrm{3x}} }\right)} \\ $$$$\mathrm{y}\left(\mathrm{o}\right)\:=\mathrm{1}\:\Rightarrow\frac{\mathrm{1}}{\left(^{\mathrm{3}} \sqrt{−\mathrm{1}+\lambda}\right)}\:=\mathrm{1}\:\Rightarrow−\mathrm{1}+\lambda\:=\mathrm{1}\:\Rightarrow\lambda\:=\mathrm{2}\:\Rightarrow \\ $$$$\mathrm{y}\left(\mathrm{x}\right)\:=\frac{\mathrm{1}}{\left(^{\mathrm{3}} \sqrt{−\mathrm{1}+\mathrm{2e}^{−\mathrm{3x}} }\right)} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *