Menu Close

solve-y-y-y-e-x-x-1-

Tinku Tara 0 Comments
Pin




Question Number 131048 by mathmax by abdo last updated on 31/Jan/21
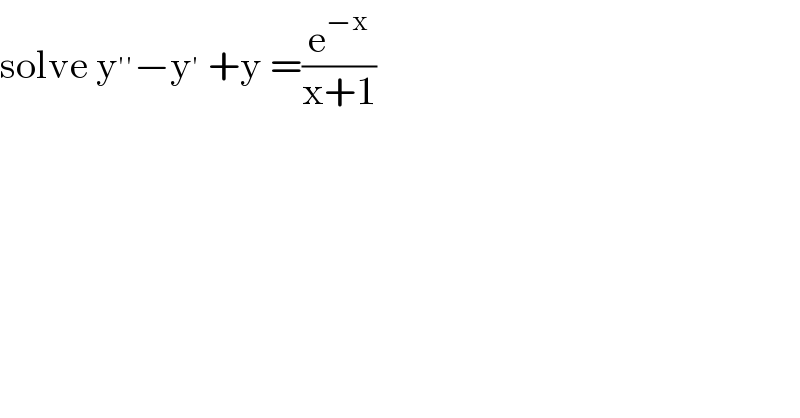
solve y^(′′) −y^′ +y =(e^(−x) /(x+1))
$$\mathrm{solve}\:\mathrm{y}^{''} −\mathrm{y}^{'} \:+\mathrm{y}\:=\frac{\mathrm{e}^{−\mathrm{x}} }{\mathrm{x}+\mathrm{1}} \\ $$
Answered by Ar Brandon last updated on 01/Feb/21
Homogenous eqn: m^2 −m+1=0 ⇒m=((1±i(√3))/2) y_(gh) =e^(x/2) (Acos(√3)x+Bsin(√3)x) By varying parameters, let y_(PI) =e^(x/2) (A(x)cos(√3)x+B(x)sin(√3)x)=au+bv We solve for a^′ and b′ in the simultaneous eqn below { ((a′u+b′v=0)),((a′u′+b′v′=(e^(−x) /(x+1)))) :} Let W(u,v)= determinant ((u,v),((u′),(v′))) = determinant (((e^(x/2) cos(√3)x),(e^(x/2) sin(√3)x)),(((1/2)e^(x/2) cos(√3)x−(√3)e^(x/2) sin(√3)x),((√3)e^(x/2) cos(√3)x+(1/2)e^(x/2) sin(√3)x))) =e^x ((√3)cos^2 (√3)x+(1/2)sin(√3)xcos(√3)x) −e^x ((1/2)sin(√3)xcos(√3)x−(√3)sin^2 (√3)x)=(√3)e^x w_u = determinant ((0,(e^(x/2) sin(√3)x)),((e^(−x) /(x+1)),((√3)e^(x/2) cos(√3)x+(1/2)e^(x/2) sin(√3)x)))=−((e^(−(x/2)) sin(√3)x)/(x+1)) w_v = determinant (((e^(x/2) cos(√3)x),0),(((1/2)e^(x/2) cos(√3)x−(√3)e^(x/2) sin(√3)x),(e^(−x) /(x+1))))=((e^(−(x/2)) cos(√3)x)/(x+1)) u=∫(w_u /W)dx , v=∫(w_v /W)dx
$$\mathrm{Homogenous}\:\mathrm{eqn}:\:\mathrm{m}^{\mathrm{2}} −\mathrm{m}+\mathrm{1}=\mathrm{0}\:\Rightarrow\mathrm{m}=\frac{\mathrm{1}\pm\mathrm{i}\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$$\mathrm{y}_{\mathrm{gh}} =\mathrm{e}^{\frac{\mathrm{x}}{\mathrm{2}}} \left(\mathrm{Acos}\sqrt{\mathrm{3}}\mathrm{x}+\mathrm{Bsin}\sqrt{\mathrm{3}}\mathrm{x}\right) \\ $$$$\mathrm{By}\:\mathrm{varying}\:\mathrm{parameters},\:\mathrm{let}\: \\ $$$$\mathrm{y}_{\mathrm{PI}} =\mathrm{e}^{\frac{\mathrm{x}}{\mathrm{2}}} \left(\mathrm{A}\left(\mathrm{x}\right)\mathrm{cos}\sqrt{\mathrm{3}}\mathrm{x}+\mathrm{B}\left(\mathrm{x}\right)\mathrm{sin}\sqrt{\mathrm{3}}\mathrm{x}\right)=\mathrm{au}+\mathrm{bv} \\ $$$$\mathrm{We}\:\mathrm{solve}\:\mathrm{for}\:\mathrm{a}^{'} \:\mathrm{and}\:\mathrm{b}'\:\mathrm{in}\:\mathrm{the}\:\mathrm{simultaneous}\:\mathrm{eqn}\:\mathrm{below} \\ $$$$\begin{cases}{\mathrm{a}'\mathrm{u}+\mathrm{b}'\mathrm{v}=\mathrm{0}}\\{\mathrm{a}'\mathrm{u}'+\mathrm{b}'\mathrm{v}'=\frac{\mathrm{e}^{−\mathrm{x}} }{\mathrm{x}+\mathrm{1}}}\end{cases} \\ $$$$\mathrm{Let}\:\mathrm{W}\left(\mathrm{u},\mathrm{v}\right)=\begin{vmatrix}{\mathrm{u}}&{\mathrm{v}}\\{\mathrm{u}'}&{\mathrm{v}'}\end{vmatrix} \\ $$$$=\begin{vmatrix}{\mathrm{e}^{\frac{\mathrm{x}}{\mathrm{2}}} \mathrm{cos}\sqrt{\mathrm{3}}\mathrm{x}}&{\mathrm{e}^{\frac{\mathrm{x}}{\mathrm{2}}} \mathrm{sin}\sqrt{\mathrm{3}}\mathrm{x}}\\{\frac{\mathrm{1}}{\mathrm{2}}\mathrm{e}^{\frac{\mathrm{x}}{\mathrm{2}}} \mathrm{cos}\sqrt{\mathrm{3}}\mathrm{x}−\sqrt{\mathrm{3}}\mathrm{e}^{\frac{\mathrm{x}}{\mathrm{2}}} \mathrm{sin}\sqrt{\mathrm{3}}\mathrm{x}}&{\sqrt{\mathrm{3}}\mathrm{e}^{\frac{\mathrm{x}}{\mathrm{2}}} \mathrm{cos}\sqrt{\mathrm{3}}\mathrm{x}+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{e}^{\frac{\mathrm{x}}{\mathrm{2}}} \mathrm{sin}\sqrt{\mathrm{3}}\mathrm{x}}\end{vmatrix} \\ $$$$=\mathrm{e}^{\mathrm{x}} \left(\sqrt{\mathrm{3}}\mathrm{cos}^{\mathrm{2}} \sqrt{\mathrm{3}}\mathrm{x}+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\sqrt{\mathrm{3}}\mathrm{xcos}\sqrt{\mathrm{3}}\mathrm{x}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\mathrm{e}^{\mathrm{x}} \left(\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\sqrt{\mathrm{3}}\mathrm{xcos}\sqrt{\mathrm{3}}\mathrm{x}−\sqrt{\mathrm{3}}\mathrm{sin}^{\mathrm{2}} \sqrt{\mathrm{3}}\mathrm{x}\right)=\sqrt{\mathrm{3}}\mathrm{e}^{\mathrm{x}} \\ $$$$\mathrm{w}_{\mathrm{u}} =\begin{vmatrix}{\mathrm{0}}&{\mathrm{e}^{\frac{\mathrm{x}}{\mathrm{2}}} \mathrm{sin}\sqrt{\mathrm{3}}\mathrm{x}}\\{\frac{\mathrm{e}^{−\mathrm{x}} }{\mathrm{x}+\mathrm{1}}}&{\sqrt{\mathrm{3}}\mathrm{e}^{\frac{\mathrm{x}}{\mathrm{2}}} \mathrm{cos}\sqrt{\mathrm{3}}\mathrm{x}+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{e}^{\frac{\mathrm{x}}{\mathrm{2}}} \mathrm{sin}\sqrt{\mathrm{3}}\mathrm{x}}\end{vmatrix}=−\frac{\mathrm{e}^{−\frac{\mathrm{x}}{\mathrm{2}}} \mathrm{sin}\sqrt{\mathrm{3}}\mathrm{x}}{\mathrm{x}+\mathrm{1}} \\ $$$$\mathrm{w}_{\mathrm{v}} =\begin{vmatrix}{\mathrm{e}^{\frac{\mathrm{x}}{\mathrm{2}}} \mathrm{cos}\sqrt{\mathrm{3}}\mathrm{x}}&{\mathrm{0}}\\{\frac{\mathrm{1}}{\mathrm{2}}\mathrm{e}^{\frac{\mathrm{x}}{\mathrm{2}}} \mathrm{cos}\sqrt{\mathrm{3}}\mathrm{x}−\sqrt{\mathrm{3}}\mathrm{e}^{\frac{\mathrm{x}}{\mathrm{2}}} \mathrm{sin}\sqrt{\mathrm{3}}\mathrm{x}}&{\frac{\mathrm{e}^{−\mathrm{x}} }{\mathrm{x}+\mathrm{1}}}\end{vmatrix}=\frac{\mathrm{e}^{−\frac{\mathrm{x}}{\mathrm{2}}} \mathrm{cos}\sqrt{\mathrm{3}}\mathrm{x}}{\mathrm{x}+\mathrm{1}} \\ $$$$\mathrm{u}=\int\frac{\mathrm{w}_{\mathrm{u}} }{\mathrm{W}}\mathrm{dx}\:,\:\mathrm{v}=\int\frac{\mathrm{w}_{\mathrm{v}} }{\mathrm{W}}\mathrm{dx} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *