Question Number 165620 by mathlove last updated on 05/Feb/22

$${solve} \\ $$$${z}^{\mathrm{7}} =−\mathrm{4} \\ $$
Answered by aleks041103 last updated on 05/Feb/22
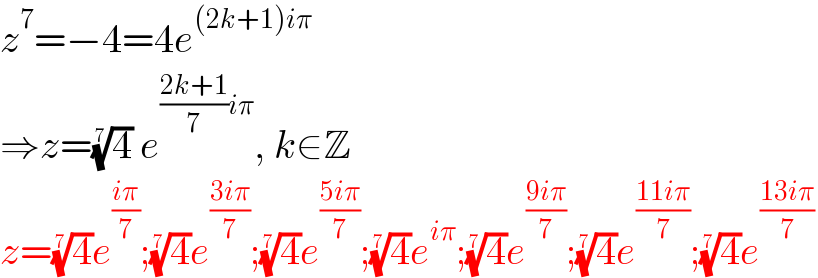
$${z}^{\mathrm{7}} =−\mathrm{4}=\mathrm{4}{e}^{\left(\mathrm{2}{k}+\mathrm{1}\right){i}\pi} \\ $$$$\Rightarrow{z}=\sqrt[{\mathrm{7}}]{\mathrm{4}}\:{e}^{\frac{\mathrm{2}{k}+\mathrm{1}}{\mathrm{7}}{i}\pi} ,\:{k}\in\mathbb{Z} \\ $$$${z}=\sqrt[{\mathrm{7}}]{\mathrm{4}}{e}^{\frac{{i}\pi}{\mathrm{7}}} ;\sqrt[{\mathrm{7}}]{\mathrm{4}}{e}^{\frac{\mathrm{3}{i}\pi}{\mathrm{7}}} ;\sqrt[{\mathrm{7}}]{\mathrm{4}}{e}^{\frac{\mathrm{5}{i}\pi}{\mathrm{7}}} ;\sqrt[{\mathrm{7}}]{\mathrm{4}}{e}^{{i}\pi} ;\sqrt[{\mathrm{7}}]{\mathrm{4}}{e}^{\frac{\mathrm{9}{i}\pi}{\mathrm{7}}} ;\sqrt[{\mathrm{7}}]{\mathrm{4}}{e}^{\frac{\mathrm{11}{i}\pi}{\mathrm{7}}} ;\sqrt[{\mathrm{7}}]{\mathrm{4}}{e}^{\frac{\mathrm{13}{i}\pi}{\mathrm{7}}\:} \\ $$
