Menu Close

solving-the-following-system-of-equations-3x-y-x-3y-x-2-3y-z-y-3z-y-2-3z-x-z-3x-z-2-

Tinku Tara 0 Comments
Pin




Question Number 119921 by bramlexs22 last updated on 28/Oct/20
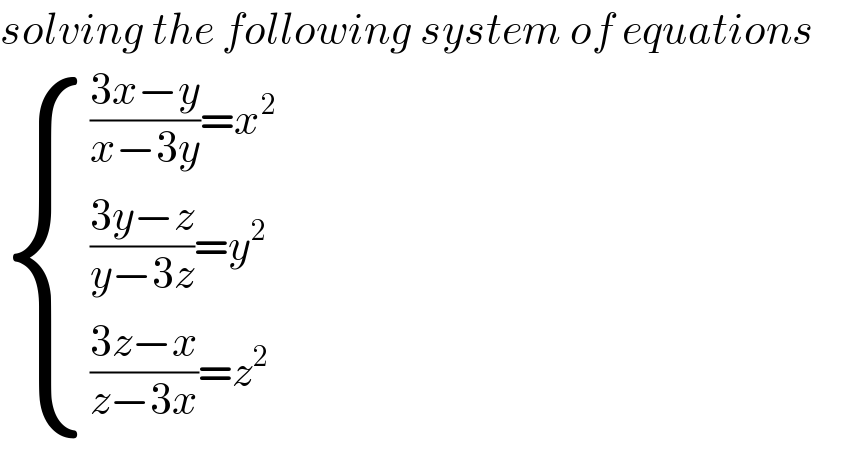
solving the following system of equations { ((((3x−y)/(x−3y))=x^2 )),((((3y−z)/(y−3z))=y^2 )),((((3z−x)/(z−3x))=z^2 )) :}
$${solving}\:{the}\:{following}\:{system}\:{of}\:{equations} \\ $$$$\begin{cases}{\frac{\mathrm{3}{x}−{y}}{{x}−\mathrm{3}{y}}={x}^{\mathrm{2}} }\\{\frac{\mathrm{3}{y}−{z}}{{y}−\mathrm{3}{z}}={y}^{\mathrm{2}} }\\{\frac{\mathrm{3}{z}−{x}}{{z}−\mathrm{3}{x}}={z}^{\mathrm{2}} }\end{cases} \\ $$
Answered by mindispower last updated on 28/Oct/20
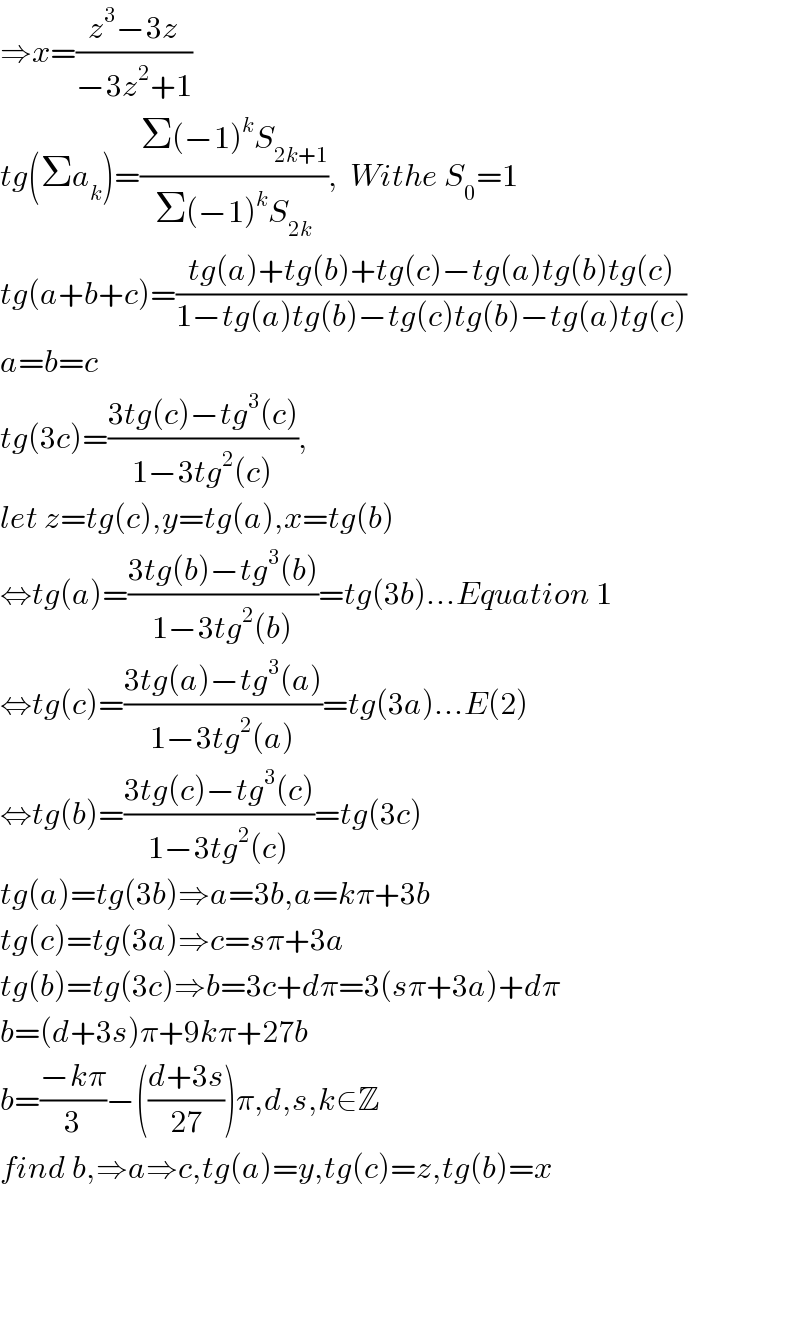
⇒x=((z^3 −3z)/(−3z^2 +1)) tg(Σa_k )=((Σ(−1)^k S_(2k+1) )/(Σ(−1)^k S_(2k) )), Withe S_0 =1 tg(a+b+c)=((tg(a)+tg(b)+tg(c)−tg(a)tg(b)tg(c))/(1−tg(a)tg(b)−tg(c)tg(b)−tg(a)tg(c))) a=b=c tg(3c)=((3tg(c)−tg^3 (c))/(1−3tg^2 (c))), let z=tg(c),y=tg(a),x=tg(b) ⇔tg(a)=((3tg(b)−tg^3 (b))/(1−3tg^2 (b)))=tg(3b)...Equation 1 ⇔tg(c)=((3tg(a)−tg^3 (a))/(1−3tg^2 (a)))=tg(3a)...E(2) ⇔tg(b)=((3tg(c)−tg^3 (c))/(1−3tg^2 (c)))=tg(3c) tg(a)=tg(3b)⇒a=3b,a=kπ+3b tg(c)=tg(3a)⇒c=sπ+3a tg(b)=tg(3c)⇒b=3c+dπ=3(sπ+3a)+dπ b=(d+3s)π+9kπ+27b b=((−kπ)/3)−(((d+3s)/(27)))π,d,s,k∈Z find b,⇒a⇒c,tg(a)=y,tg(c)=z,tg(b)=x
$$\Rightarrow{x}=\frac{{z}^{\mathrm{3}} −\mathrm{3}{z}}{−\mathrm{3}{z}^{\mathrm{2}} +\mathrm{1}} \\ $$$${tg}\left(\Sigma{a}_{{k}} \right)=\frac{\Sigma\left(−\mathrm{1}\right)^{{k}} {S}_{\mathrm{2}{k}+\mathrm{1}} }{\Sigma\left(−\mathrm{1}\right)^{{k}} {S}_{\mathrm{2}{k}} },\:\:{Withe}\:{S}_{\mathrm{0}} =\mathrm{1} \\ $$$${tg}\left({a}+{b}+{c}\right)=\frac{{tg}\left({a}\right)+{tg}\left({b}\right)+{tg}\left({c}\right)−{tg}\left({a}\right){tg}\left({b}\right){tg}\left({c}\right)}{\mathrm{1}−{tg}\left({a}\right){tg}\left({b}\right)−{tg}\left({c}\right){tg}\left({b}\right)−{tg}\left({a}\right){tg}\left({c}\right)} \\ $$$${a}={b}={c} \\ $$$${tg}\left(\mathrm{3}{c}\right)=\frac{\mathrm{3}{tg}\left({c}\right)−{tg}^{\mathrm{3}} \left({c}\right)}{\mathrm{1}−\mathrm{3}{tg}^{\mathrm{2}} \left({c}\right)}, \\ $$$${let}\:{z}={tg}\left({c}\right),{y}={tg}\left({a}\right),{x}={tg}\left({b}\right) \\ $$$$\Leftrightarrow{tg}\left({a}\right)=\frac{\mathrm{3}{tg}\left({b}\right)−{tg}^{\mathrm{3}} \left({b}\right)}{\mathrm{1}−\mathrm{3}{tg}^{\mathrm{2}} \left({b}\right)}={tg}\left(\mathrm{3}{b}\right)…{Equation}\:\mathrm{1} \\ $$$$\Leftrightarrow{tg}\left({c}\right)=\frac{\mathrm{3}{tg}\left({a}\right)−{tg}^{\mathrm{3}} \left({a}\right)}{\mathrm{1}−\mathrm{3}{tg}^{\mathrm{2}} \left({a}\right)}={tg}\left(\mathrm{3}{a}\right)…{E}\left(\mathrm{2}\right) \\ $$$$\Leftrightarrow{tg}\left({b}\right)=\frac{\mathrm{3}{tg}\left({c}\right)−{tg}^{\mathrm{3}} \left({c}\right)}{\mathrm{1}−\mathrm{3}{tg}^{\mathrm{2}} \left({c}\right)}={tg}\left(\mathrm{3}{c}\right) \\ $$$${tg}\left({a}\right)={tg}\left(\mathrm{3}{b}\right)\Rightarrow{a}=\mathrm{3}{b},{a}={k}\pi+\mathrm{3}{b} \\ $$$${tg}\left({c}\right)={tg}\left(\mathrm{3}{a}\right)\Rightarrow{c}={s}\pi+\mathrm{3}{a} \\ $$$${tg}\left({b}\right)={tg}\left(\mathrm{3}{c}\right)\Rightarrow{b}=\mathrm{3}{c}+{d}\pi=\mathrm{3}\left({s}\pi+\mathrm{3}{a}\right)+{d}\pi \\ $$$${b}=\left({d}+\mathrm{3}{s}\right)\pi+\mathrm{9}{k}\pi+\mathrm{27}{b} \\ $$$${b}=\frac{−{k}\pi}{\mathrm{3}}−\left(\frac{{d}+\mathrm{3}{s}}{\mathrm{27}}\right)\pi,{d},{s},{k}\in\mathbb{Z} \\ $$$${find}\:{b},\Rightarrow{a}\Rightarrow{c},{tg}\left({a}\right)={y},{tg}\left({c}\right)={z},{tg}\left({b}\right)={x} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Answered by MJS_new last updated on 28/Oct/20
one solution is x=y=z=±i for the other solutions let y=px∧z=qx ⇒ { ((((p−3)/(3p−1))=x^2 )),((((3p−q)/(p−3q))=p^2 x^2 )),((((3q−1)/(q−3))=q^2 x^2 )) :} ⇒ ((p−3)/(3p−1))=((3p−q)/(p^2 (p−3q)))=((3q−1)/(q^2 (q−3))) we can eliminate one of the two unknown and get a polynome of degree 13 with one solution =1. the other 12 are ∈R but I only can approximate q=((p(p^3 −3p^2 −9p+3))/(3p^3 −9p^2 −3p+1)) (p−1)((p^(12) +1)−20(p^(11) +p)+34(p^(10) +p^2 )+700(p^9 +p^3 )−2705(p^8 +p^4 )−680(p^7 +p^5 )+9436p^6 )=0 p_1 =1 p_2 ≈−5.87781 p_3 ≈−1.63530 p_4 ≈−.611508 p_5 ≈−.170131 p_6 ≈.0637272 p_7 ≈.199046 p_8 ≈.278216 p_9 ≈.320163 p_(10) ≈3.12340 p_(11) ≈3.59433 p_(12) ≈5.02397 p_(13) ≈15.6919 please do the rest for yourself
$$\mathrm{one}\:\mathrm{solution}\:\mathrm{is}\:{x}={y}={z}=\pm\mathrm{i} \\ $$$$\mathrm{for}\:\mathrm{the}\:\mathrm{other}\:\mathrm{solutions}\:\mathrm{let} \\ $$$${y}={px}\wedge{z}={qx} \\ $$$$\Rightarrow \\ $$$$\begin{cases}{\frac{{p}−\mathrm{3}}{\mathrm{3}{p}−\mathrm{1}}={x}^{\mathrm{2}} }\\{\frac{\mathrm{3}{p}−{q}}{{p}−\mathrm{3}{q}}={p}^{\mathrm{2}} {x}^{\mathrm{2}} }\\{\frac{\mathrm{3}{q}−\mathrm{1}}{{q}−\mathrm{3}}={q}^{\mathrm{2}} {x}^{\mathrm{2}} }\end{cases} \\ $$$$\Rightarrow \\ $$$$\frac{{p}−\mathrm{3}}{\mathrm{3}{p}−\mathrm{1}}=\frac{\mathrm{3}{p}−{q}}{{p}^{\mathrm{2}} \left({p}−\mathrm{3}{q}\right)}=\frac{\mathrm{3}{q}−\mathrm{1}}{{q}^{\mathrm{2}} \left({q}−\mathrm{3}\right)} \\ $$$$\mathrm{we}\:\mathrm{can}\:\mathrm{eliminate}\:\mathrm{one}\:\mathrm{of}\:\mathrm{the}\:\mathrm{two}\:\mathrm{unknown} \\ $$$$\mathrm{and}\:\mathrm{get}\:\mathrm{a}\:\mathrm{polynome}\:\mathrm{of}\:\mathrm{degree}\:\mathrm{13}\:\mathrm{with}\:\mathrm{one} \\ $$$$\mathrm{solution}\:=\mathrm{1}.\:\mathrm{the}\:\mathrm{other}\:\mathrm{12}\:\mathrm{are}\:\in\mathbb{R}\:\mathrm{but}\:\mathrm{I}\:\mathrm{only} \\ $$$$\mathrm{can}\:\mathrm{approximate} \\ $$$${q}=\frac{{p}\left({p}^{\mathrm{3}} −\mathrm{3}{p}^{\mathrm{2}} −\mathrm{9}{p}+\mathrm{3}\right)}{\mathrm{3}{p}^{\mathrm{3}} −\mathrm{9}{p}^{\mathrm{2}} −\mathrm{3}{p}+\mathrm{1}} \\ $$$$\left({p}−\mathrm{1}\right)\left(\left({p}^{\mathrm{12}} +\mathrm{1}\right)−\mathrm{20}\left({p}^{\mathrm{11}} +{p}\right)+\mathrm{34}\left({p}^{\mathrm{10}} +{p}^{\mathrm{2}} \right)+\mathrm{700}\left({p}^{\mathrm{9}} +{p}^{\mathrm{3}} \right)−\mathrm{2705}\left({p}^{\mathrm{8}} +{p}^{\mathrm{4}} \right)−\mathrm{680}\left({p}^{\mathrm{7}} +{p}^{\mathrm{5}} \right)+\mathrm{9436}{p}^{\mathrm{6}} \right)=\mathrm{0} \\ $$$${p}_{\mathrm{1}} =\mathrm{1} \\ $$$${p}_{\mathrm{2}} \approx−\mathrm{5}.\mathrm{87781} \\ $$$${p}_{\mathrm{3}} \approx−\mathrm{1}.\mathrm{63530} \\ $$$${p}_{\mathrm{4}} \approx−.\mathrm{611508} \\ $$$${p}_{\mathrm{5}} \approx−.\mathrm{170131} \\ $$$${p}_{\mathrm{6}} \approx.\mathrm{0637272} \\ $$$${p}_{\mathrm{7}} \approx.\mathrm{199046} \\ $$$${p}_{\mathrm{8}} \approx.\mathrm{278216} \\ $$$${p}_{\mathrm{9}} \approx.\mathrm{320163} \\ $$$${p}_{\mathrm{10}} \approx\mathrm{3}.\mathrm{12340} \\ $$$${p}_{\mathrm{11}} \approx\mathrm{3}.\mathrm{59433} \\ $$$${p}_{\mathrm{12}} \approx\mathrm{5}.\mathrm{02397} \\ $$$${p}_{\mathrm{13}} \approx\mathrm{15}.\mathrm{6919} \\ $$$$\mathrm{please}\:\mathrm{do}\:\mathrm{the}\:\mathrm{rest}\:\mathrm{for}\:\mathrm{yourself} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *