Question Number 45802 by MJS last updated on 17/Oct/18
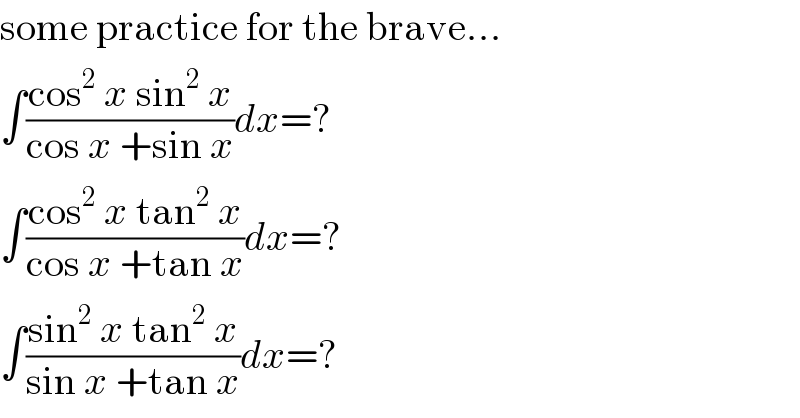
$$\mathrm{some}\:\mathrm{practice}\:\mathrm{for}\:\mathrm{the}\:\mathrm{brave}… \\ $$$$\int\frac{\mathrm{cos}^{\mathrm{2}} \:{x}\:\mathrm{sin}^{\mathrm{2}} \:{x}}{\mathrm{cos}\:{x}\:+\mathrm{sin}\:{x}}{dx}=? \\ $$$$\int\frac{\mathrm{cos}^{\mathrm{2}} \:{x}\:\mathrm{tan}^{\mathrm{2}} \:{x}}{\mathrm{cos}\:{x}\:+\mathrm{tan}\:{x}}{dx}=? \\ $$$$\int\frac{\mathrm{sin}^{\mathrm{2}} \:{x}\:\mathrm{tan}^{\mathrm{2}} \:{x}}{\mathrm{sin}\:{x}\:+\mathrm{tan}\:{x}}{dx}=? \\ $$
Commented by maxmathsup by imad last updated on 17/Oct/18

$$\left.\mathrm{1}\right)\:{changement}\:{tan}\left(\frac{{x}}{\mathrm{2}}\right)={t}\:{give}\:\:\: \\ $$$$\int\:\:\frac{{cos}^{\mathrm{2}} {x}\:{sin}^{\mathrm{2}} {x}}{{cosx}\:+{sinx}}{dx}\:=\int\:\:\:\:\:\frac{\left(\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }\right)^{\mathrm{2}} \:\frac{\mathrm{4}{t}^{\mathrm{2}} }{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{\mathrm{2}} }}{\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }+\frac{\mathrm{2}{t}}{\mathrm{1}+{t}^{\mathrm{2}} }}\:\frac{\mathrm{2}{dt}}{\mathrm{1}+{t}^{\mathrm{2}} } \\ $$$$=\:\mathrm{8}\int\:\:\:\:\:\:\frac{{t}^{\mathrm{2}} \left(\mathrm{1}−{t}^{\mathrm{2}} \right)^{\mathrm{2}} }{\left(\mathrm{1}−{t}^{\mathrm{2}} +\mathrm{2}{t}\right)}\:{dt}\:=\mathrm{8}\:\:\int\:\:\:\:\:\:\frac{{t}^{\mathrm{2}} \left({t}^{\mathrm{4}} −\mathrm{2}{t}^{\mathrm{2}} \:+\mathrm{1}\right)}{−\left({t}^{\mathrm{2}} −\mathrm{2}{t}−\mathrm{1}\right)}{dt} \\ $$$$=−\mathrm{8}\:\int\:\:\:\:\frac{{t}^{\mathrm{6}} −\mathrm{2}{t}^{\mathrm{4}} \:+{t}^{\mathrm{2}} }{\left({t}^{\mathrm{2}} −\mathrm{2}{t}\:−\mathrm{1}\right)}{dt}\:=−\mathrm{8}\:\int\:\:\:\frac{{t}^{\mathrm{4}} \left({t}^{\mathrm{2}} −\mathrm{2}{t}−\mathrm{1}\right)+\mathrm{2}{t}^{\mathrm{5}} +{t}^{\mathrm{4}} −\mathrm{2}{t}^{\mathrm{4}} +{t}^{\mathrm{2}} }{{t}^{\mathrm{2}} −\mathrm{2}{t}−\mathrm{1}}{dt} \\ $$$$=−\mathrm{8}\:\int\:{t}^{\mathrm{4}} {dt}\:−\mathrm{8}\:\int\:\frac{\mathrm{2}{t}^{\mathrm{5}} −{t}^{\mathrm{4}} \:+{t}^{\mathrm{2}} }{{t}^{\mathrm{2}} −\mathrm{2}{t}−\mathrm{1}}{dt} \\ $$$$=−\frac{\mathrm{8}}{\mathrm{5}}{t}^{\mathrm{5}} \:−\mathrm{8}\:\int\:\:\frac{\mathrm{2}{t}^{\mathrm{3}} \left({t}^{\mathrm{2}} −\mathrm{2}{t}−\mathrm{1}\right)+\mathrm{4}{t}^{\mathrm{4}} +\mathrm{2}{t}^{\mathrm{3}} −{t}^{\mathrm{4}} +{t}^{\mathrm{2}} }{{t}^{\mathrm{2}} −\mathrm{2}{t}−\mathrm{1}}{dt} \\ $$$$=−\frac{\mathrm{8}}{\mathrm{5}}{t}^{\mathrm{5}} \:−\mathrm{16}\:\int\:{t}^{\mathrm{3}} {dt}\:−\mathrm{8}\:\int\:\:\frac{\mathrm{3}{t}^{\mathrm{4}} \:+\mathrm{2}{t}^{\mathrm{3}} \:+{t}^{\mathrm{2}} }{{t}^{\mathrm{2}} −\mathrm{2}{t}−\mathrm{1}}{dt} \\ $$$$=−\frac{\mathrm{8}}{\mathrm{5}}{t}^{\mathrm{5}} −\mathrm{4}\:{t}^{\mathrm{4}} \:\:\:−\mathrm{8}\:\int\:\:\frac{\mathrm{3}{t}^{\mathrm{2}} \left({t}^{\mathrm{2}} −\mathrm{2}{t}−\mathrm{1}\right)\:+\mathrm{6}{t}^{\mathrm{3}} \:+\mathrm{3}{t}^{\mathrm{2}} \:+\mathrm{2}{t}^{\mathrm{3}} \:+{t}^{\mathrm{2}} }{{t}^{\mathrm{2}} −\mathrm{2}{t}−\mathrm{1}}{dt} \\ $$$$=−\frac{\mathrm{8}}{\mathrm{5}}{t}^{\mathrm{5}} \:−\mathrm{4}{t}^{\mathrm{4}} \:−\mathrm{24}\:\int\:{t}^{\mathrm{2}} {dt}\:−\mathrm{8}\:\int\:\:\frac{\mathrm{8}{t}^{\mathrm{3}} \:+\mathrm{4}{t}^{\mathrm{2}} }{{t}^{\mathrm{2}} −\mathrm{2}{t}−\mathrm{1}}{dt} \\ $$$$=−\frac{\mathrm{8}}{\mathrm{5}}{t}^{\mathrm{5}} −\mathrm{4}{t}^{\mathrm{4}} \:−\mathrm{8}\:{t}^{\mathrm{3}} \:−\mathrm{32}\:\int\:\:\:\frac{\mathrm{2}{t}^{\mathrm{3}} \:+{t}^{\mathrm{2}} }{{t}^{\mathrm{2}} −\mathrm{2}{t}\:−\mathrm{1}}{dt}\:{but} \\ $$$$\int\:\:\:\frac{\mathrm{2}{t}^{\mathrm{3}} \:+{t}^{\mathrm{2}} }{{t}^{\mathrm{2}} −\mathrm{2}{t}−\mathrm{1}}{dt}\:=\:\int\:\:\frac{\mathrm{2}{t}\left({t}^{\mathrm{2}} −\mathrm{2}{t}−\mathrm{1}\right)\:+\mathrm{4}{t}^{\mathrm{2}} \:+\mathrm{2}{t}\:+{t}^{\mathrm{2}} }{{t}^{\mathrm{2}} −\mathrm{2}{t}−\mathrm{1}}{dt} \\ $$$$=\:{t}^{\mathrm{2}} \:\:+\:\int\:\frac{\mathrm{5}{t}^{\mathrm{2}} \:+\mathrm{2}{t}}{{t}^{\mathrm{2}} −\mathrm{2}{t}−\mathrm{1}}{dt}\:={t}^{\mathrm{2}} \:+\int\:\:\frac{\mathrm{5}\left({t}^{\mathrm{2}} −\mathrm{2}{t}+\mathrm{1}\right)+\mathrm{10}{t}\:−\mathrm{5}\:+\mathrm{2}{t}}{{t}^{\mathrm{2}} −\mathrm{2}{t}−\mathrm{1}}{dt} \\ $$$$={t}^{\mathrm{2}} \:+\mathrm{5}{t}\:\:+\int\:\:\:\frac{\mathrm{12}{t}−\mathrm{5}}{{t}^{\mathrm{2}} −\mathrm{2}{t}−\mathrm{1}}{dt}\:{also}\: \\ $$$$\int\:\frac{\mathrm{12}{t}−\mathrm{5}}{{t}^{\mathrm{2}} −\mathrm{2}{t}−\mathrm{1}}{dt}\:=\:\mathrm{6}\:\:\int\:\frac{\mathrm{2}{t}−\mathrm{2}−\frac{\mathrm{5}}{\mathrm{6}}+\mathrm{2}}{{t}^{\mathrm{2}} −\mathrm{2}{t}−\mathrm{1}}{dt}\:=\mathrm{6}{ln}\mid{t}^{\mathrm{2}} −\mathrm{2}{t}−\mathrm{1}\mid\:+\mathrm{7}\:\int\:\frac{{dt}}{\left({t}−\mathrm{1}\right)^{\mathrm{2}} −\mathrm{2}} \\ $$$$=\mathrm{6}\:{ln}\mid{t}^{\mathrm{2}} −\mathrm{2}{t}−\mathrm{1}\mid\:+\mathrm{7}\:\int\:\:\:\:\frac{{dt}}{\left({t}−\mathrm{3}\right)\left({t}+\mathrm{1}\right)} \\ $$$$=\mathrm{6}{ln}\mid{t}^{\mathrm{2}} −\mathrm{2}{t}−\mathrm{1}\mid\:+\frac{\mathrm{7}}{\mathrm{4}}\:\int\:\left(\frac{\mathrm{1}}{{t}−\mathrm{3}}\:−\frac{\mathrm{1}}{{t}+\mathrm{1}}\right){dt} \\ $$$$=\mathrm{6}{ln}\mid{t}^{\mathrm{2}} −\mathrm{2}{t}−\mathrm{1}\mid\:+\frac{\mathrm{7}}{\mathrm{4}}{ln}\mid\frac{{t}−\mathrm{3}}{{t}+\mathrm{1}}\mid\:\:\:{with}\:{t}={tan}\left(\frac{{x}}{\mathrm{2}}\right)\:\:…. \\ $$$$ \\ $$
