Question Number 128090 by ajfour last updated on 04/Jan/21
![someone help cheking this: x^3 =x+c let x=(p−2q)+(q−2p) = −(p+q) p^3 −8q^3 −6pq(p−2q)+ q^3 −8p^3 −6pq(q−2p)+ 3(p−2q)(q−2p)[(p−2q)+(q−2p)] = (p−2q)+(q−2p)+c ⇒ −7(p^3 +q^3 )+6pq(p+q) −3(p+q)[5pq−2(p^2 +q^2 )] +(p+q) = c let p^3 +q^3 =−(c/7) And since x=−(p+q) so with −x^3 =−x−c we have p^3 +q^3 +3pq(p+q)=p+q−c ⇒ (3pq−1)(p+q)=−((6c)/7) 1−9pq+6(p^2 +q^2 )=0 (p^2 +q^2 )(p+q)−pq(p+q)=−(c/7) say p^2 +q^2 =t , then pq=((1+6t)/9) ; p+q=(((−((6c)/7)))/(((1+6t)/3)−1)) p+q=((9c)/(7(1−3t))) p^2 +q^2 =(p+q)^2 −2pq t=[((9c)/(7(1−3t)))]^2 −((2(1+6t))/9) [((9c)/(7(1−3t)))]^2 =((21t+2)/9) ⇒ (21t+2)(3t−1)^2 =(((27c)/7))^2 .....](https://www.tinkutara.com/question/Q128090.png)
$${someone}\:{help}\:{cheking}\:{this}: \\ $$$$\:\:\:\:{x}^{\mathrm{3}} ={x}+{c}\:\: \\ $$$${let}\:\:{x}=\left({p}−\mathrm{2}{q}\right)+\left({q}−\mathrm{2}{p}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:=\:−\left({p}+{q}\right) \\ $$$${p}^{\mathrm{3}} −\mathrm{8}{q}^{\mathrm{3}} −\mathrm{6}{pq}\left({p}−\mathrm{2}{q}\right)+ \\ $$$${q}^{\mathrm{3}} −\mathrm{8}{p}^{\mathrm{3}} −\mathrm{6}{pq}\left({q}−\mathrm{2}{p}\right)+ \\ $$$$\mathrm{3}\left({p}−\mathrm{2}{q}\right)\left({q}−\mathrm{2}{p}\right)\left[\left({p}−\mathrm{2}{q}\right)+\left({q}−\mathrm{2}{p}\right)\right] \\ $$$$\:\:\:\:\:\:\:\:=\:\left({p}−\mathrm{2}{q}\right)+\left({q}−\mathrm{2}{p}\right)+{c} \\ $$$$\Rightarrow \\ $$$$−\mathrm{7}\left({p}^{\mathrm{3}} +{q}^{\mathrm{3}} \right)+\mathrm{6}{pq}\left({p}+{q}\right) \\ $$$$−\mathrm{3}\left({p}+{q}\right)\left[\mathrm{5}{pq}−\mathrm{2}\left({p}^{\mathrm{2}} +{q}^{\mathrm{2}} \right)\right] \\ $$$$+\left({p}+{q}\right)\:=\:{c} \\ $$$${let}\:\:{p}^{\mathrm{3}} +{q}^{\mathrm{3}} =−\frac{{c}}{\mathrm{7}} \\ $$$${And}\:{since}\:\:\:{x}=−\left({p}+{q}\right) \\ $$$${so}\:{with}\:\:−{x}^{\mathrm{3}} =−{x}−{c}\:\:\:{we}\:{have} \\ $$$${p}^{\mathrm{3}} +{q}^{\mathrm{3}} +\mathrm{3}{pq}\left({p}+{q}\right)={p}+{q}−{c} \\ $$$$\Rightarrow\:\:\:\left(\mathrm{3}{pq}−\mathrm{1}\right)\left({p}+{q}\right)=−\frac{\mathrm{6}{c}}{\mathrm{7}} \\ $$$$\:\:\mathrm{1}−\mathrm{9}{pq}+\mathrm{6}\left({p}^{\mathrm{2}} +{q}^{\mathrm{2}} \right)=\mathrm{0} \\ $$$$\left({p}^{\mathrm{2}} +{q}^{\mathrm{2}} \right)\left({p}+{q}\right)−{pq}\left({p}+{q}\right)=−\frac{{c}}{\mathrm{7}} \\ $$$${say}\:\:{p}^{\mathrm{2}} +{q}^{\mathrm{2}} ={t}\:\:,\:{then} \\ $$$${pq}=\frac{\mathrm{1}+\mathrm{6}{t}}{\mathrm{9}}\:\:;\:\:{p}+{q}=\frac{\left(−\frac{\mathrm{6}{c}}{\mathrm{7}}\right)}{\frac{\mathrm{1}+\mathrm{6}{t}}{\mathrm{3}}−\mathrm{1}} \\ $$$${p}+{q}=\frac{\mathrm{9}{c}}{\mathrm{7}\left(\mathrm{1}−\mathrm{3}{t}\right)} \\ $$$${p}^{\mathrm{2}} +{q}^{\mathrm{2}} =\left({p}+{q}\right)^{\mathrm{2}} −\mathrm{2}{pq} \\ $$$${t}=\left[\frac{\mathrm{9}{c}}{\mathrm{7}\left(\mathrm{1}−\mathrm{3}{t}\right)}\right]^{\mathrm{2}} −\frac{\mathrm{2}\left(\mathrm{1}+\mathrm{6}{t}\right)}{\mathrm{9}} \\ $$$$\left[\frac{\mathrm{9}{c}}{\mathrm{7}\left(\mathrm{1}−\mathrm{3}{t}\right)}\right]^{\mathrm{2}} =\frac{\mathrm{21}{t}+\mathrm{2}}{\mathrm{9}} \\ $$$$\Rightarrow\:\:\:\left(\mathrm{21}{t}+\mathrm{2}\right)\left(\mathrm{3}{t}−\mathrm{1}\right)^{\mathrm{2}} =\left(\frac{\mathrm{27}{c}}{\mathrm{7}}\right)^{\mathrm{2}} \\ $$$$….. \\ $$
Commented by MJS_new last updated on 04/Jan/21
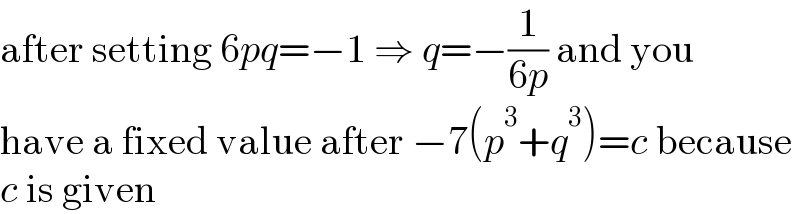
$$\mathrm{after}\:\mathrm{setting}\:\mathrm{6}{pq}=−\mathrm{1}\:\Rightarrow\:{q}=−\frac{\mathrm{1}}{\mathrm{6}{p}}\:\mathrm{and}\:\mathrm{you} \\ $$$$\mathrm{have}\:\mathrm{a}\:\mathrm{fixed}\:\mathrm{value}\:\mathrm{after}\:−\mathrm{7}\left({p}^{\mathrm{3}} +{q}^{\mathrm{3}} \right)={c}\:\mathrm{because} \\ $$$${c}\:\mathrm{is}\:\mathrm{given} \\ $$
Commented by MJS_new last updated on 04/Jan/21
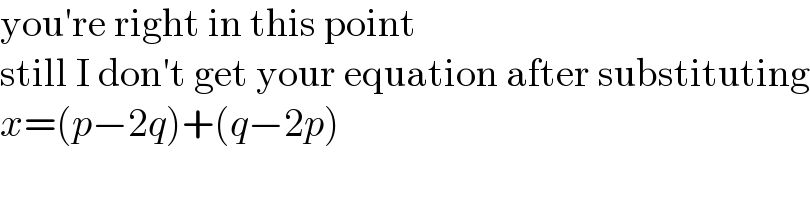
$$\mathrm{you}'\mathrm{re}\:\mathrm{right}\:\mathrm{in}\:\mathrm{this}\:\mathrm{point} \\ $$$$\mathrm{still}\:\mathrm{I}\:\mathrm{don}'\mathrm{t}\:\mathrm{get}\:\mathrm{your}\:\mathrm{equation}\:\mathrm{after}\:\mathrm{substituting} \\ $$$${x}=\left({p}−\mathrm{2}{q}\right)+\left({q}−\mathrm{2}{p}\right) \\ $$
