Question Number 63894 by mathmax by abdo last updated on 10/Jul/19
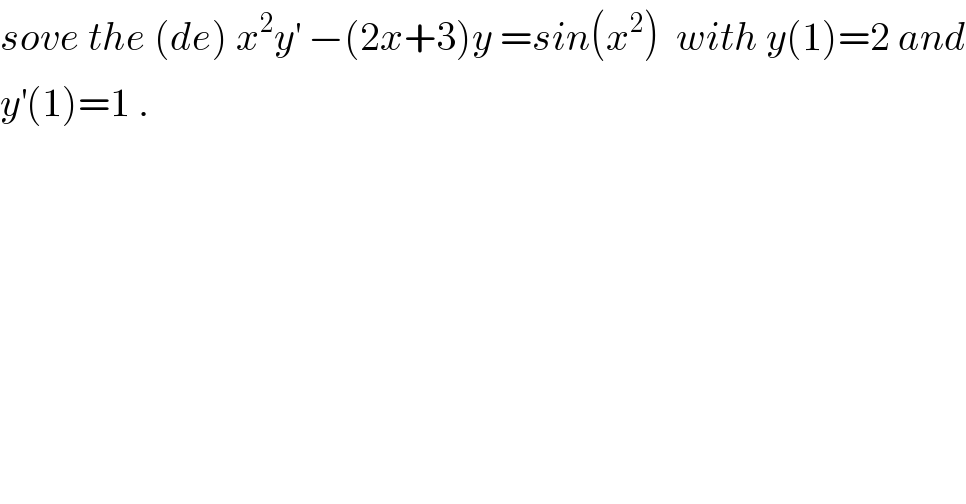
$${sove}\:{the}\:\left({de}\right)\:{x}^{\mathrm{2}} {y}^{'} \:−\left(\mathrm{2}{x}+\mathrm{3}\right){y}\:={sin}\left({x}^{\mathrm{2}} \right)\:\:{with}\:{y}\left(\mathrm{1}\right)=\mathrm{2}\:{and} \\ $$$${y}^{'} \left(\mathrm{1}\right)=\mathrm{1}\:. \\ $$
Commented by mathmax by abdo last updated on 11/Jul/19
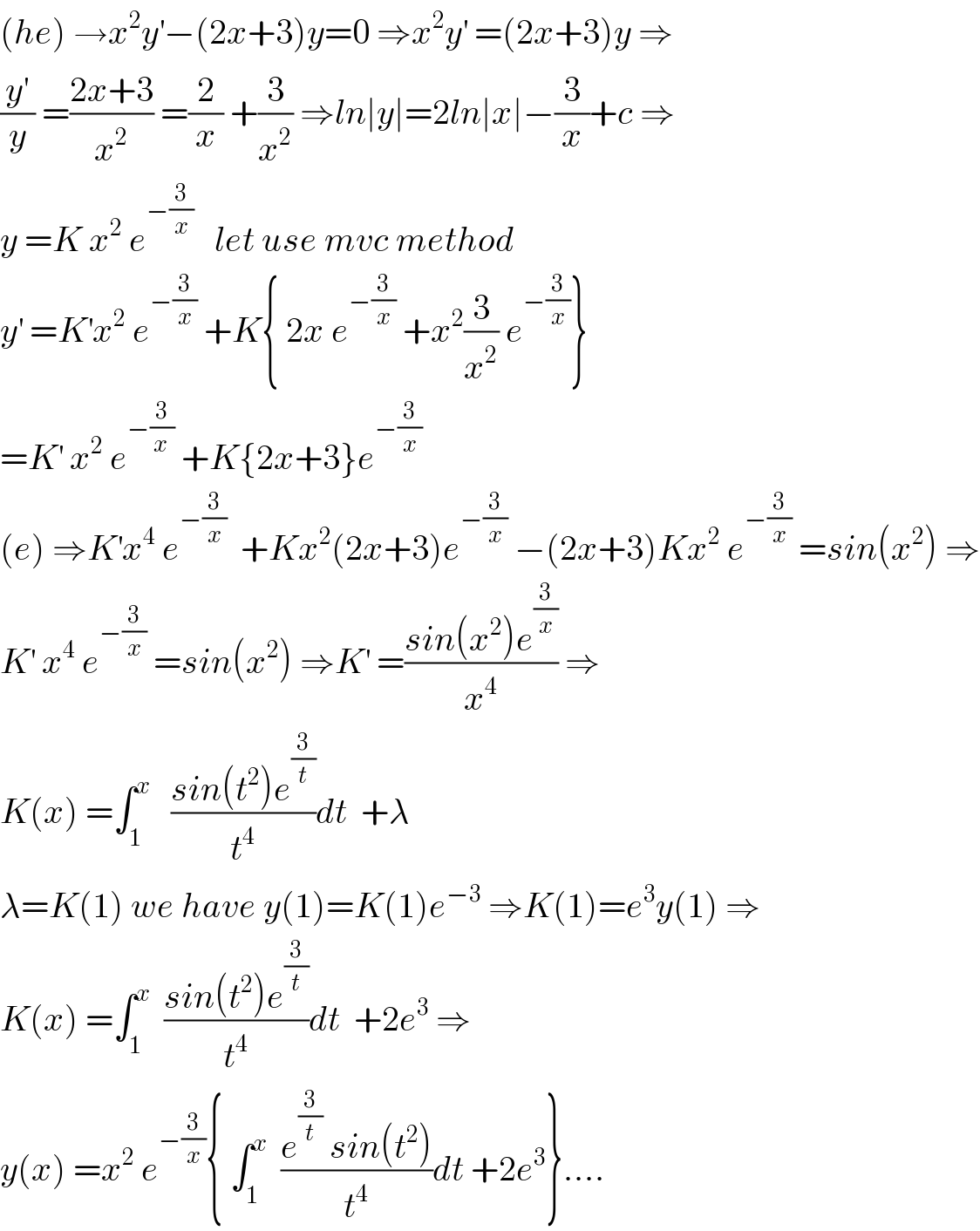
$$\left({he}\right)\:\rightarrow{x}^{\mathrm{2}} {y}^{'} −\left(\mathrm{2}{x}+\mathrm{3}\right){y}=\mathrm{0}\:\Rightarrow{x}^{\mathrm{2}} {y}^{'} \:=\left(\mathrm{2}{x}+\mathrm{3}\right){y}\:\Rightarrow \\ $$$$\frac{{y}^{'} }{{y}}\:=\frac{\mathrm{2}{x}+\mathrm{3}}{{x}^{\mathrm{2}} }\:=\frac{\mathrm{2}}{{x}}\:+\frac{\mathrm{3}}{{x}^{\mathrm{2}} }\:\Rightarrow{ln}\mid{y}\mid=\mathrm{2}{ln}\mid{x}\mid−\frac{\mathrm{3}}{{x}}+{c}\:\Rightarrow \\ $$$${y}\:={K}\:{x}^{\mathrm{2}} \:{e}^{−\frac{\mathrm{3}}{{x}}} \:\:\:{let}\:{use}\:{mvc}\:{method}\: \\ $$$${y}^{'} \:={K}^{'} {x}^{\mathrm{2}} \:{e}^{−\frac{\mathrm{3}}{{x}}} \:+{K}\left\{\:\mathrm{2}{x}\:{e}^{−\frac{\mathrm{3}}{{x}}} \:+{x}^{\mathrm{2}} \frac{\mathrm{3}}{{x}^{\mathrm{2}} }\:{e}^{−\frac{\mathrm{3}}{{x}}} \right\} \\ $$$$={K}^{'} \:{x}^{\mathrm{2}} \:{e}^{−\frac{\mathrm{3}}{{x}\:}} \:+{K}\left\{\mathrm{2}{x}+\mathrm{3}\right\}{e}^{−\frac{\mathrm{3}}{{x}}} \\ $$$$\left({e}\right)\:\Rightarrow{K}^{'} {x}^{\mathrm{4}} \:{e}^{−\frac{\mathrm{3}}{{x}}} \:\:+{Kx}^{\mathrm{2}} \left(\mathrm{2}{x}+\mathrm{3}\right){e}^{−\frac{\mathrm{3}}{{x}}} \:−\left(\mathrm{2}{x}+\mathrm{3}\right){Kx}^{\mathrm{2}} \:{e}^{−\frac{\mathrm{3}}{{x}}} \:={sin}\left({x}^{\mathrm{2}} \right)\:\Rightarrow \\ $$$${K}^{'} \:{x}^{\mathrm{4}} \:{e}^{−\frac{\mathrm{3}}{{x}}} \:={sin}\left({x}^{\mathrm{2}} \right)\:\Rightarrow{K}^{'} \:=\frac{{sin}\left({x}^{\mathrm{2}} \right){e}^{\frac{\mathrm{3}}{{x}}} }{{x}^{\mathrm{4}} }\:\Rightarrow \\ $$$${K}\left({x}\right)\:=\int_{\mathrm{1}} ^{{x}} \:\:\:\frac{{sin}\left({t}^{\mathrm{2}} \right){e}^{\frac{\mathrm{3}}{{t}}} }{{t}^{\mathrm{4}} }{dt}\:\:+\lambda \\ $$$$\lambda={K}\left(\mathrm{1}\right)\:{we}\:{have}\:{y}\left(\mathrm{1}\right)={K}\left(\mathrm{1}\right){e}^{−\mathrm{3}} \:\Rightarrow{K}\left(\mathrm{1}\right)={e}^{\mathrm{3}} {y}\left(\mathrm{1}\right)\:\Rightarrow \\ $$$${K}\left({x}\right)\:=\int_{\mathrm{1}} ^{{x}} \:\:\frac{{sin}\left({t}^{\mathrm{2}} \right){e}^{\frac{\mathrm{3}}{{t}}} }{{t}^{\mathrm{4}} }{dt}\:\:+\mathrm{2}{e}^{\mathrm{3}} \:\Rightarrow \\ $$$${y}\left({x}\right)\:={x}^{\mathrm{2}} \:{e}^{−\frac{\mathrm{3}}{{x}}} \left\{\:\int_{\mathrm{1}} ^{{x}} \:\:\frac{{e}^{\frac{\mathrm{3}}{{t}}} \:{sin}\left({t}^{\mathrm{2}} \right)}{{t}^{\mathrm{4}} }{dt}\:+\mathrm{2}{e}^{\mathrm{3}} \right\}…. \\ $$
