Question Number 107401 by mathmax by abdo last updated on 10/Aug/20
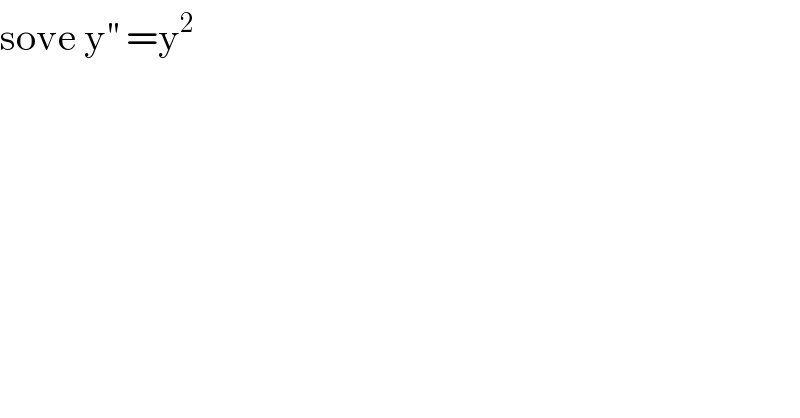
$$\mathrm{sove}\:\mathrm{y}^{''} \:=\mathrm{y}^{\mathrm{2}} \\ $$
Answered by mr W last updated on 10/Aug/20

$${y}''={y}'\frac{{d}\left({y}'\right)}{{dy}}={u}\frac{{du}}{{dy}} \\ $$$${u}\frac{{du}}{{dy}}={y}^{\mathrm{2}} \\ $$$$\Rightarrow\frac{{u}^{\mathrm{2}} }{\mathrm{2}}=\frac{{y}^{\mathrm{3}} }{\mathrm{3}}+{C}_{\mathrm{1}} \\ $$$$\Rightarrow{u}^{\mathrm{2}} =\frac{\mathrm{2}}{\mathrm{3}}\left({y}^{\mathrm{3}} +{C}_{\mathrm{1}} \right) \\ $$$$\Rightarrow{u}=\frac{{dy}}{{dx}}=\pm\sqrt{\frac{\mathrm{2}}{\mathrm{3}}}×\sqrt{{y}^{\mathrm{3}} +{C}_{\mathrm{1}} } \\ $$$$\Rightarrow\pm\sqrt{\frac{\mathrm{3}}{\mathrm{2}}}\frac{{dy}}{\:\sqrt{{y}^{\mathrm{3}} +{C}_{\mathrm{1}} }}={dx} \\ $$$$\Rightarrow\pm\sqrt{\frac{\mathrm{3}}{\mathrm{2}}}\int\frac{{dy}}{\:\sqrt{{y}^{\mathrm{3}} +{C}_{\mathrm{1}} }}=\int{dx} \\ $$$$\Rightarrow{x}=\pm\sqrt{\frac{\mathrm{3}}{\mathrm{2}}}\int\frac{{dy}}{\:\sqrt{{y}^{\mathrm{3}} +{C}_{\mathrm{1}} }}+{C}_{\mathrm{2}} \\ $$
