Question Number 62438 by mathsolverby Abdo last updated on 21/Jun/19
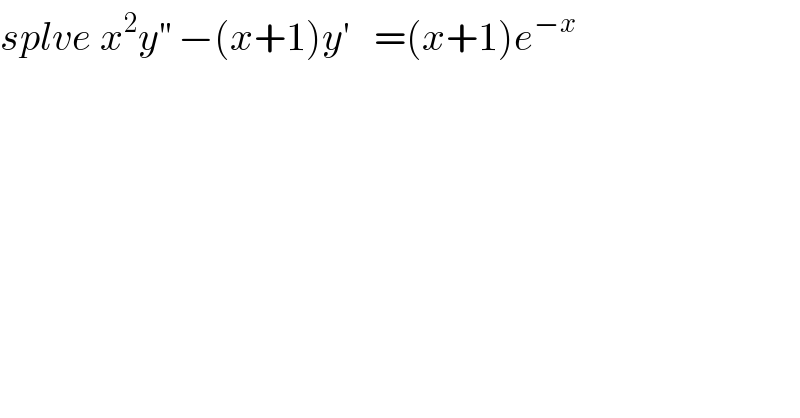
$${splve}\:{x}^{\mathrm{2}} {y}^{''} \:−\left({x}+\mathrm{1}\right){y}'\:\:\:=\left({x}+\mathrm{1}\right){e}^{−{x}} \\ $$$$ \\ $$$$ \\ $$
Commented by mathmax by abdo last updated on 27/Jul/19
![let y^′ =z (e) ⇒x^2 z^′ −(x+1)z =(x+1)e^(−x) (he) ⇒x^2 z^′ −(x+1)z =0 ⇒x^2 z^′ =(x+1)z ⇒(z^′ /z) =((x+1)/x^2 ) =(1/x) +(1/x^2 ) ⇒ln∣z∣ =ln∣x∣−(1/x) +c ⇒z = k∣x∣e^(−(1/x)) let determine the solution on ]0,+∞[ ⇒z(x) =kx e^(−(1/x)) mvc method →z^′ =k^′ x e^(−(1/x)) +k{e^(−(1/x)) +x(1/x^2 )e^(−(1/x)) } ={k^′ x +k +(k/x)}e^(−(1/x)) (e) ⇒x^2 {k^′ x +k +(k/x)}e^(−(1/x)) −(x+1)kx e^(−(1/x)) =(x+1)e^(−x) ⇒ {k^′ x^3 +kx^2 + kx−kx^2 −kx}e^(−(1/x)) =(x+1)e^(−x) ⇒ k^′ x^3 =(x+1)e^(−x+(1/x)) ⇒k^′ =((x+1)/x^3 ) e^((1−x^2 )/x) ⇒k(x) =∫_. ^x ((t+1)/t^3 )e^((1−t^2 )/t) dt +λ ⇒z(x) =x e^(−(1/x)) { ∫_. ^x ((t+1)/t^3 )e^((1−t^2 )/t) dt +λ}=λx e^(−(1/x)) +xe^(−(1/x)) ∫_. ^x ((t+1)/t^3 )e^((1−t^2 )/t) dt y^′ (x)=z(x) ⇒y(x) =∫ z(x)dx +C y(x)=∫ λx e^(−(1/x)) dx +∫ (xe^(−(1/x)) ∫_. ^x ((t+1)/t^3 ) e^((1−t^2 )/t) dt)dx +C .](https://www.tinkutara.com/question/Q65294.png)
$${let}\:{y}^{'} \:={z}\:\:\left({e}\right)\:\Rightarrow{x}^{\mathrm{2}} {z}^{'} −\left({x}+\mathrm{1}\right){z}\:=\left({x}+\mathrm{1}\right){e}^{−{x}} \\ $$$$\left({he}\right)\:\Rightarrow{x}^{\mathrm{2}} {z}^{'} −\left({x}+\mathrm{1}\right){z}\:=\mathrm{0}\:\Rightarrow{x}^{\mathrm{2}} {z}^{'} \:=\left({x}+\mathrm{1}\right){z}\:\Rightarrow\frac{{z}^{'} }{{z}}\:=\frac{{x}+\mathrm{1}}{{x}^{\mathrm{2}} }\:=\frac{\mathrm{1}}{{x}}\:+\frac{\mathrm{1}}{{x}^{\mathrm{2}} } \\ $$$$\Rightarrow{ln}\mid{z}\mid\:={ln}\mid{x}\mid−\frac{\mathrm{1}}{{x}}\:+{c}\:\Rightarrow{z}\:=\:{k}\mid{x}\mid{e}^{−\frac{\mathrm{1}}{{x}}} \\ $$$$\left.{let}\:{determine}\:{the}\:{solution}\:{on}\:\right]\mathrm{0},+\infty\left[\:\Rightarrow{z}\left({x}\right)\:={kx}\:{e}^{−\frac{\mathrm{1}}{{x}}} \right. \\ $$$${mvc}\:{method}\:\rightarrow{z}^{'} \:={k}^{'} {x}\:{e}^{−\frac{\mathrm{1}}{{x}}} \:+{k}\left\{{e}^{−\frac{\mathrm{1}}{{x}}} \:+{x}\frac{\mathrm{1}}{{x}^{\mathrm{2}} }{e}^{−\frac{\mathrm{1}}{{x}}} \right\} \\ $$$$=\left\{{k}^{'} {x}\:+{k}\:\:+\frac{{k}}{{x}}\right\}{e}^{−\frac{\mathrm{1}}{{x}}} \\ $$$$\left({e}\right)\:\Rightarrow{x}^{\mathrm{2}} \left\{{k}^{'} {x}\:+{k}\:+\frac{{k}}{{x}}\right\}{e}^{−\frac{\mathrm{1}}{{x}}} \:−\left({x}+\mathrm{1}\right){kx}\:{e}^{−\frac{\mathrm{1}}{{x}}} \:=\left({x}+\mathrm{1}\right){e}^{−{x}} \:\Rightarrow \\ $$$$\left\{{k}^{'} \:{x}^{\mathrm{3}} \:+{kx}^{\mathrm{2}} +\:{kx}−{kx}^{\mathrm{2}} −{kx}\right\}{e}^{−\frac{\mathrm{1}}{{x}}} \:=\left({x}+\mathrm{1}\right){e}^{−{x}} \:\Rightarrow \\ $$$${k}^{'} {x}^{\mathrm{3}} \:=\left({x}+\mathrm{1}\right){e}^{−{x}+\frac{\mathrm{1}}{{x}}} \:\Rightarrow{k}^{'} \:=\frac{{x}+\mathrm{1}}{{x}^{\mathrm{3}} }\:{e}^{\frac{\mathrm{1}−{x}^{\mathrm{2}} }{{x}}} \:\:\Rightarrow{k}\left({x}\right)\:=\int_{.} ^{{x}} \:\frac{{t}+\mathrm{1}}{{t}^{\mathrm{3}} }{e}^{\frac{\mathrm{1}−{t}^{\mathrm{2}} }{{t}}} \:{dt}\:+\lambda \\ $$$$\Rightarrow{z}\left({x}\right)\:={x}\:{e}^{−\frac{\mathrm{1}}{{x}}} \left\{\:\int_{.} ^{{x}} \:\frac{{t}+\mathrm{1}}{{t}^{\mathrm{3}} }{e}^{\frac{\mathrm{1}−{t}^{\mathrm{2}} }{{t}}} {dt}\:+\lambda\right\}=\lambda{x}\:{e}^{−\frac{\mathrm{1}}{{x}}} \:+{xe}^{−\frac{\mathrm{1}}{{x}}} \:\int_{.} ^{{x}} \:\frac{{t}+\mathrm{1}}{{t}^{\mathrm{3}} }{e}^{\frac{\mathrm{1}−{t}^{\mathrm{2}} }{{t}}} \:{dt} \\ $$$${y}^{'} \left({x}\right)={z}\left({x}\right)\:\Rightarrow{y}\left({x}\right)\:=\int\:{z}\left({x}\right){dx}\:+{C} \\ $$$${y}\left({x}\right)=\int\:\:\lambda{x}\:{e}^{−\frac{\mathrm{1}}{{x}}} \:{dx}\:\:\:+\int\:\:\:\:\left({xe}^{−\frac{\mathrm{1}}{{x}}} \:\int_{.} ^{{x}} \:\frac{{t}+\mathrm{1}}{{t}^{\mathrm{3}} }\:{e}^{\frac{\mathrm{1}−{t}^{\mathrm{2}} }{{t}}} \:{dt}\right){dx}\:+{C}\:. \\ $$$$ \\ $$
