Question Number 35238 by abdo.msup.com last updated on 17/May/18
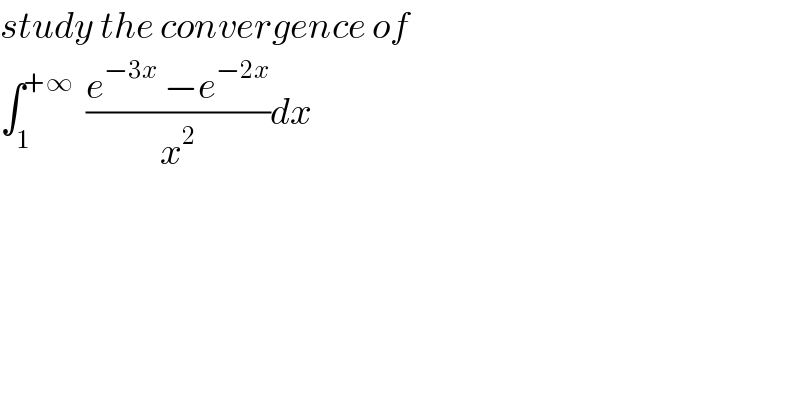
$${study}\:{the}\:{convergence}\:{of} \\ $$$$\int_{\mathrm{1}} ^{+\infty} \:\:\frac{{e}^{−\mathrm{3}{x}} \:−{e}^{−\mathrm{2}{x}} }{{x}^{\mathrm{2}} }{dx}\: \\ $$
Commented by prof Abdo imad last updated on 20/May/18
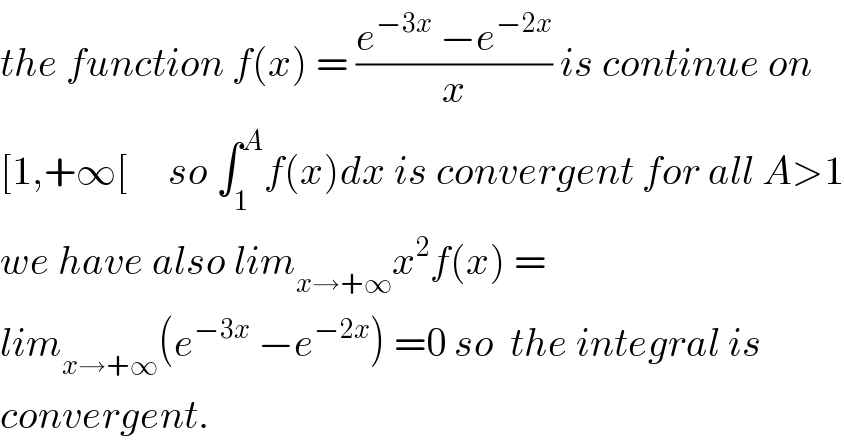
$${the}\:{function}\:{f}\left({x}\right)\:=\:\frac{{e}^{−\mathrm{3}{x}} \:−{e}^{−\mathrm{2}{x}} }{{x}}\:{is}\:{continue}\:{on} \\ $$$$\left[\mathrm{1},+\infty\left[\:\:\:\:\:{so}\:\int_{\mathrm{1}} ^{{A}} {f}\left({x}\right){dx}\:{is}\:{convergent}\:{for}\:{all}\:{A}>\mathrm{1}\right.\right. \\ $$$${we}\:{have}\:{also}\:{lim}_{{x}\rightarrow+\infty} {x}^{\mathrm{2}} {f}\left({x}\right)\:= \\ $$$${lim}_{{x}\rightarrow+\infty} \left({e}^{−\mathrm{3}{x}} \:−{e}^{−\mathrm{2}{x}} \right)\:=\mathrm{0}\:{so}\:\:{the}\:{integral}\:{is} \\ $$$${convergent}. \\ $$
