Question Number 42187 by maxmathsup by imad last updated on 19/Aug/18
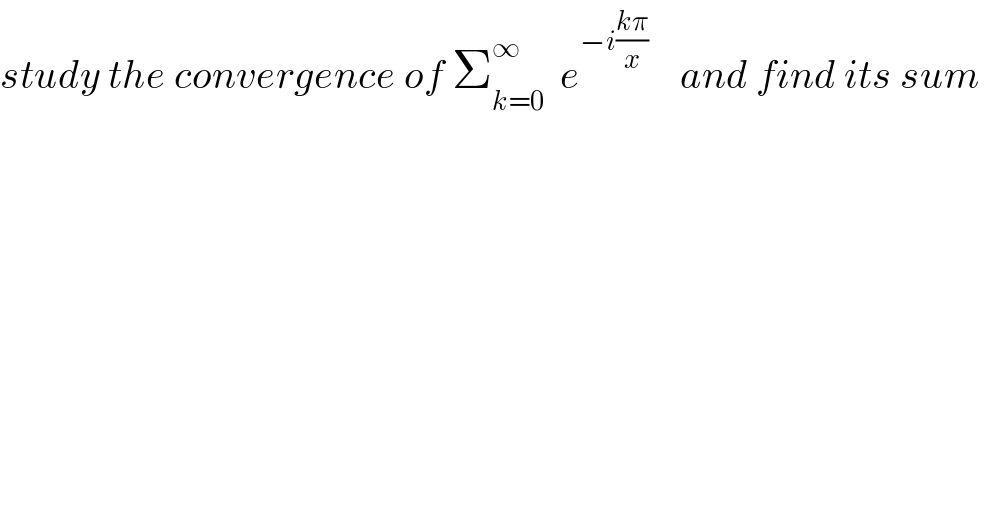
$${study}\:{the}\:{convergence}\:{of}\:\sum_{{k}=\mathrm{0}} ^{\infty} \:\:{e}^{−{i}\frac{{k}\pi}{{x}}} \:\:\:\:{and}\:{find}\:{its}\:{sum}\: \\ $$
Commented by maxmathsup by imad last updated on 22/Aug/18
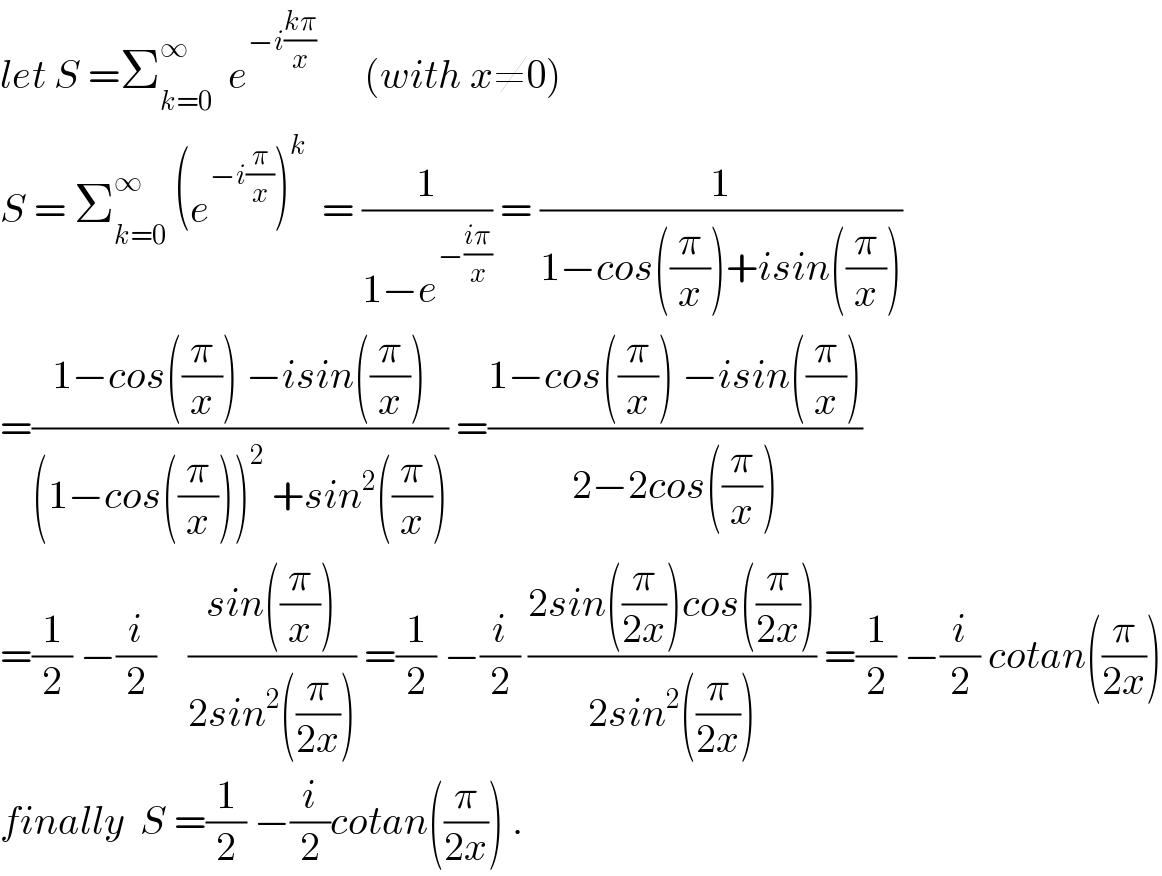
$${let}\:{S}\:=\sum_{{k}=\mathrm{0}} ^{\infty} \:\:{e}^{−{i}\frac{{k}\pi}{{x}}} \:\:\:\:\:\:\left({with}\:{x}\neq\mathrm{0}\right) \\ $$$${S}\:=\:\sum_{{k}=\mathrm{0}} ^{\infty} \:\left({e}^{−{i}\frac{\pi}{{x}}} \right)^{{k}} \:\:=\:\frac{\mathrm{1}}{\mathrm{1}−{e}^{−\frac{{i}\pi}{{x}}} }\:=\:\frac{\mathrm{1}}{\mathrm{1}−{cos}\left(\frac{\pi}{{x}}\right)+{isin}\left(\frac{\pi}{{x}}\right)} \\ $$$$=\frac{\mathrm{1}−{cos}\left(\frac{\pi}{{x}}\right)\:−{isin}\left(\frac{\pi}{{x}}\right)}{\left(\mathrm{1}−{cos}\left(\frac{\pi}{{x}}\right)\right)^{\mathrm{2}} \:+{sin}^{\mathrm{2}} \left(\frac{\pi}{{x}}\right)}\:=\frac{\mathrm{1}−{cos}\left(\frac{\pi}{{x}}\right)\:−{isin}\left(\frac{\pi}{{x}}\right)}{\mathrm{2}−\mathrm{2}{cos}\left(\frac{\pi}{{x}}\right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\:−\frac{{i}}{\mathrm{2}}\:\:\:\:\frac{{sin}\left(\frac{\pi}{{x}}\right)}{\mathrm{2}{sin}^{\mathrm{2}} \left(\frac{\pi}{\mathrm{2}{x}}\right)}\:=\frac{\mathrm{1}}{\mathrm{2}}\:−\frac{{i}}{\mathrm{2}}\:\frac{\mathrm{2}{sin}\left(\frac{\pi}{\mathrm{2}{x}}\right){cos}\left(\frac{\pi}{\mathrm{2}{x}}\right)}{\mathrm{2}{sin}^{\mathrm{2}} \left(\frac{\pi}{\mathrm{2}{x}}\right)}\:=\frac{\mathrm{1}}{\mathrm{2}}\:−\frac{{i}}{\mathrm{2}}\:{cotan}\left(\frac{\pi}{\mathrm{2}{x}}\right) \\ $$$${finally}\:\:{S}\:=\frac{\mathrm{1}}{\mathrm{2}}\:−\frac{{i}}{\mathrm{2}}{cotan}\left(\frac{\pi}{\mathrm{2}{x}}\right)\:. \\ $$
