study-the-integral-0-sin-n-x-x-n-dx-n-integr-and-n-2-

Question Number 116554 by Bird last updated on 04/Oct/20

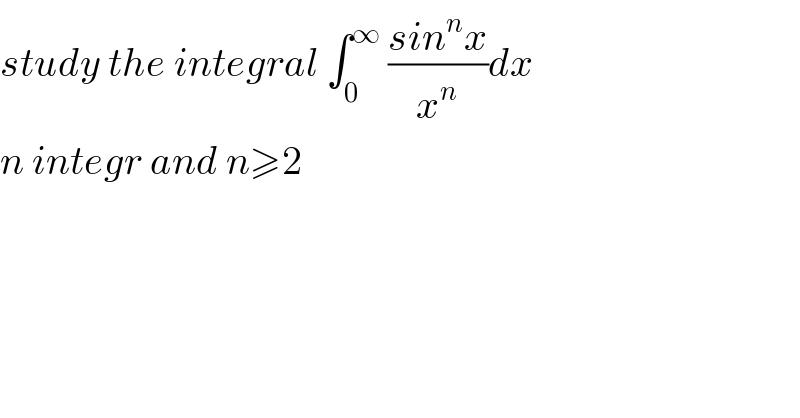
s t u d y t h e i n t e g r a l \int_{0}^{\infty} \frac{{s i n}^{n} x}{x^{n}} d x

n i n t e g r a n d n ⩾ 2

Answered by Olaf last updated on 05/Oct/20

I_{2 n} = \frac{n π}{(2 n)!} \underset{k = 1}{\sum^{n}} C_{2 n}^{n - k} {(- 1)}^{n - k} k^{2 n - 1}

I_{2 n + 1} = \frac{π}{2 (2 n)!} \underset{k = 0}{\sum^{n}} C_{2 n + 1}^{n - k} {(- 1)}^{n - k} {(k + \frac{1}{2})}^{2 n}

The demonstration is very long and

not so easy for this kind of apps .

Facebook Tweet Pin