study-the-integral-1-cos-2-x-2-1-dx-

Question Number 60967 by maxmathsup by imad last updated on 27/May/19

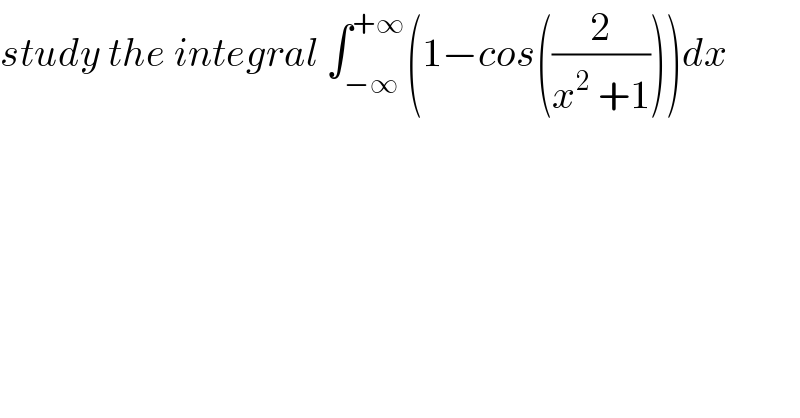
s t u d y t h e i n t e g r a l \int_{- \infty}^{+ \infty} (1 - c o s (\frac{2}{x^{2} + 1})) d x

Commented by abdo mathsup 649 cc last updated on 28/May/19

w e h a v e c o s u = \sum_{n = 0}^{\infty} \frac{{(- 1)}^{n} u^{2 n}}{(2 n)!}

= 1 - \frac{u^{2}}{2} + \frac{u^{4}}{4!} - \dots \Rightarrow - c o s u = - 1 + \frac{u^{2}}{2} - \frac{u^{4}}{4!} + \dots \Rightarrow

1 - c o s u = \frac{u^{2}}{2} - \frac{u^{4}}{4!} + \dots \Rightarrow \frac{u^{2}}{2} - \frac{u^{4}}{4!} ⩽ 1 - c o s u ⩽ \frac{u^{2}}{2} \Rightarrow

u = \frac{2}{x^{2} + 1} \Rightarrow \frac{1}{2} {(\frac{2}{x^{2} + 1})}^{2} - \frac{1}{4!} {(\frac{2}{x^{2} + 1})}^{4} ⩽ 1 - c o s (\frac{2}{x^{2} + 1})

⩽ \frac{1}{2} {(\frac{2}{x^{2} + 1})}^{2} \Rightarrow \frac{2}{{(x^{2} + 1)}^{2}} - \frac{16}{4!} \frac{1}{{(x^{2} + 1)}^{4}}

⩽ 1 - c o s (\frac{2}{x^{2} + 1}) ⩽ \frac{2}{{(x^{2} + 1)}^{2}}

\frac{16}{4!} = \frac{16}{4.3.2} = \frac{4}{3.2} = \frac{2}{3} \Rightarrow

\int_{0}^{\infty} \frac{2 d x}{{(x^{2} + 1)}^{2}} - \frac{2}{3} \int_{0}^{\infty} \frac{d x}{{(x^{2} + 1)}^{4}} ⩽ \int_{0}^{\infty} (1 - c o s (\frac{2}{x^{2} + 1})) d x

⩽ \int_{0}^{\infty} \frac{2 d x}{{(x^{2} + 1)}^{2}} \Rightarrow

4 \int_{0}^{\infty} \frac{d x}{{(x^{2} + 1)}^{2}} - \frac{4}{3} \int_{0}^{\infty} \frac{d x}{{(x^{2} + 1)}^{4}} ⩽ I ⩽ 4 \int_{0}^{\infty} \frac{d x}{{(x^{2} + 1)}^{2}}

\int_{0}^{\infty} \frac{d x}{{(x^{2} + 1)}^{2}} =_{x = t a n θ} \int_{0}^{\frac{π}{2}} \frac{1 + {t a n}^{2} θ}{{(1 + {t a n}^{2} θ)}^{2}} d θ

= \int_{0}^{\frac{π}{2}} \frac{d θ}{1 + {t a n}^{2} θ} = \int_{0}^{\frac{π}{2}} {c o s}^{2} θ d θ = \int_{0}^{\frac{π}{2}} \frac{1 + c o s (2 θ)}{2} d θ

= \frac{π}{4} + \frac{1}{4} [s i n {(2 θ]}_{0}^{\frac{π}{2}} = \frac{π}{4} + 0 = \frac{π}{4}

\int_{0}^{\infty} \frac{d x}{{(x^{2} + 1)}^{4}} =_{x = t a n θ} \int_{0}^{\frac{π}{2}} \frac{1 + {t a n}^{2} θ}{{(1 + {t a n}^{2} θ)}^{4}} d θ

= \int_{0}^{\frac{π}{2}} \frac{d θ}{{(1 + {t a n}^{2} θ)}^{3}} = \int_{0}^{\frac{π}{2}} {c o s}^{6} θ d θ

= \int_{0}^{\frac{π}{2}} {(\frac{1 + c o s (2 θ)}{2})}^{3} d θ

= \frac{1}{8} \int_{0}^{\frac{π}{2}} (1 + 3 c o s (2 θ) + 3 {c o s}^{2} (2 θ) + {c o s}^{3} (2 θ)) d θ

= \frac{π}{16} + \frac{3}{8} \int_{0}^{\frac{π}{2}} c o s (2 θ) d θ + \frac{1}{8} \int_{0}^{\frac{π}{2}} {c o s}^{3} (2 θ) d θ

= \frac{π}{16} + \frac{3}{16} {[s i n (2 θ)]}_{0}^{\frac{π}{2}} + \frac{1}{8} \int_{0}^{\frac{π}{2}} {c o s}^{3} (2 θ) d θ

= \frac{π}{16} + \frac{1}{8} \int_{0}^{\frac{π}{2}} {c o s}^{3} (2 θ) d θ

Commented by abdo mathsup 649 cc last updated on 28/May/19

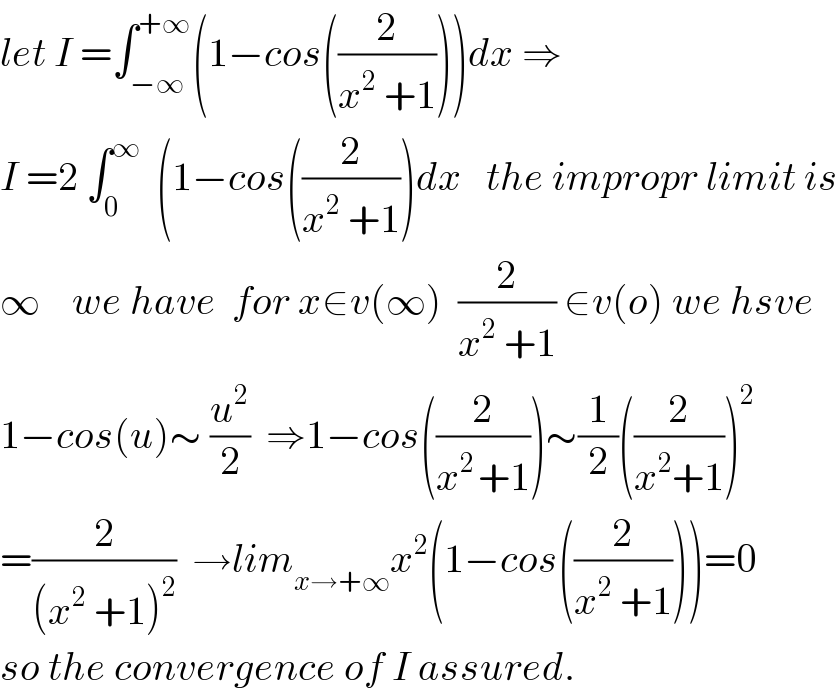
l e t I = \int_{- \infty}^{+ \infty} (1 - c o s (\frac{2}{x^{2} + 1})) d x \Rightarrow

I = 2 \int_{0}^{\infty} (1 - c o s (\frac{2}{x^{2} + 1}) d x t h e i m p r o p r l i m i t i s

\infty w e h a v e f o r x \in v (\infty) \frac{2}{x^{2} + 1} \in v (o) w e h s v e

1 - c o s (u) \sim \frac{u^{2}}{2} \Rightarrow 1 - c o s (\frac{2}{x^{2} + 1}) \sim \frac{1}{2} {(\frac{2}{x^{2} + 1})}^{2}

= \frac{2}{{(x^{2} + 1)}^{2}} \to {l i m}_{x \to + \infty} x^{2} (1 - c o s (\frac{2}{x^{2} + 1})) = 0

s o t h e c o n v e r g e n c e o f I a s s u r e d .

Commented by abdo mathsup 649 cc last updated on 28/May/19

w e h a v e {c o s}^{3} x = {(\frac{e^{i x} + e^{- i x}}{2})}^{3} = \frac{1}{8} {(e^{i x} + e^{- i x})}^{3}

= \frac{1}{8} (e^{3 i x} + 3 e^{2 i x} e^{- i x} + 3 e^{i x} e^{- 2 i x} + e^{- 3 i x})

= \frac{1}{8} (2 c o s (3 x) + 3 (2 c o s (x)))

= \frac{1}{4} c o s (3 x) + \frac{3}{4} c o s (x) \Rightarrow

\int_{0}^{\frac{π}{2}} {c o s}^{3} (2 θ) d θ = \int_{0}^{\frac{π}{2}} (\frac{1}{4} c o s (6 x) + \frac{3}{4} c o s (2 θ)) d θ

= \frac{1}{24} {[s i n (6 x)]}_{0}^{\frac{π}{2}} + \frac{3}{8} {[s i n (2 θ)]}_{0}^{\frac{π}{2}} = 0 \Rightarrow

π - \frac{4}{3} \frac{π}{16} ⩽ I ⩽ π \Rightarrow π - \frac{π}{12} ⩽ I ⩽ π \Rightarrow

\frac{11 π}{12} ⩽ I ⩽ π w e c a n t a k e v_{0} = \frac{\frac{11 π}{12} + π}{2}

= \frac{23 π}{24} a s a p p r o x i m a t e v a l u e o f

\int_{- \infty}^{+ \infty} (1 - c o s (\frac{2}{x^{2} + 1})) d x

Commented by abdo mathsup 649 cc last updated on 28/May/19

I \sim 3, 01