Sum-1-1-1-1-2-1-1-2-3-1-1-2-3-8016-

Question Number 79635 by TawaTawa last updated on 26/Jan/20

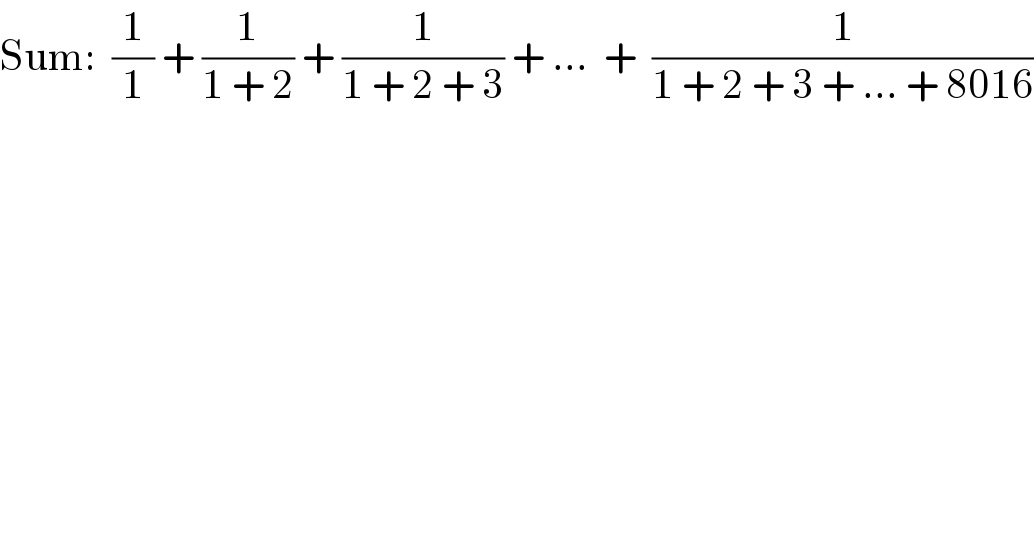
$$\mathrm{Sum}:\:\:\frac{\mathrm{1}}{\mathrm{1}}\:+\:\frac{\mathrm{1}}{\mathrm{1}\:+\:\mathrm{2}}\:+\:\frac{\mathrm{1}}{\mathrm{1}\:+\:\mathrm{2}\:+\:\mathrm{3}}\:+\:…\:\:+\:\:\frac{\mathrm{1}}{\mathrm{1}\:+\:\mathrm{2}\:+\:\mathrm{3}\:+\:…\:+\:\mathrm{8016}} \\ $$

Commented by mr W last updated on 26/Jan/20

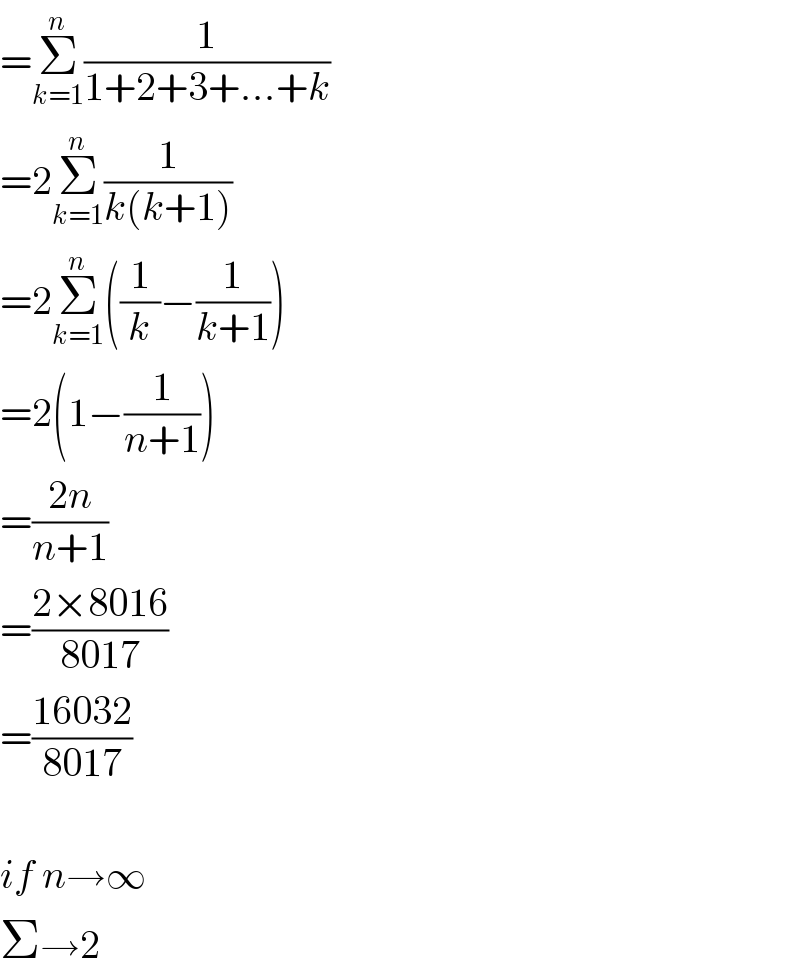
=Σ_(k=1) ^n (1/(1+2+3+...+k)) =2Σ_(k=1) ^n (1/(k(k+1))) =2Σ_(k=1) ^n ((1/k)−(1/(k+1))) =2(1−(1/(n+1))) =((2n)/(n+1)) =((2×8016)/(8017)) =((16032)/(8017)) if n→∞ Σ→2

$$=\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{\mathrm{1}+\mathrm{2}+\mathrm{3}+…+{k}} \\ $$$$=\mathrm{2}\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{{k}\left({k}+\mathrm{1}\right)} \\ $$$$=\mathrm{2}\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\left(\frac{\mathrm{1}}{{k}}−\frac{\mathrm{1}}{{k}+\mathrm{1}}\right) \\ $$$$=\mathrm{2}\left(\mathrm{1}−\frac{\mathrm{1}}{{n}+\mathrm{1}}\right) \\ $$$$=\frac{\mathrm{2}{n}}{{n}+\mathrm{1}} \\ $$$$=\frac{\mathrm{2}×\mathrm{8016}}{\mathrm{8017}} \\ $$$$=\frac{\mathrm{16032}}{\mathrm{8017}} \\ $$$$ \\ $$$${if}\:{n}\rightarrow\infty \\ $$$$\Sigma\rightarrow\mathrm{2} \\ $$

Commented by TawaTawa last updated on 26/Jan/20

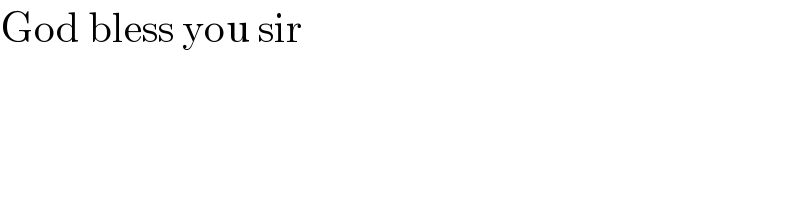
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$

Commented by TawaTawa last updated on 26/Jan/20

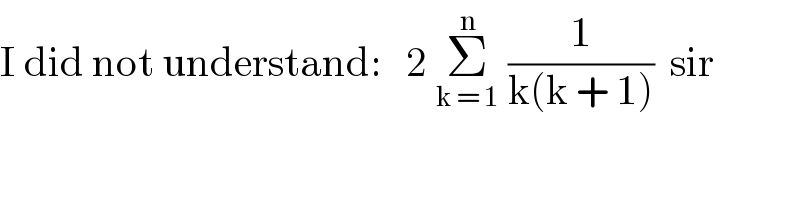
I did not understand: 2 Σ_(k = 1) ^n (1/(k(k + 1))) sir

$$\mathrm{I}\:\mathrm{did}\:\mathrm{not}\:\mathrm{understand}:\:\:\:\mathrm{2}\:\underset{\mathrm{k}\:=\:\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\:\frac{\mathrm{1}}{\mathrm{k}\left(\mathrm{k}\:+\:\mathrm{1}\right)}\:\:\mathrm{sir} \\ $$

Commented by mr W last updated on 26/Jan/20

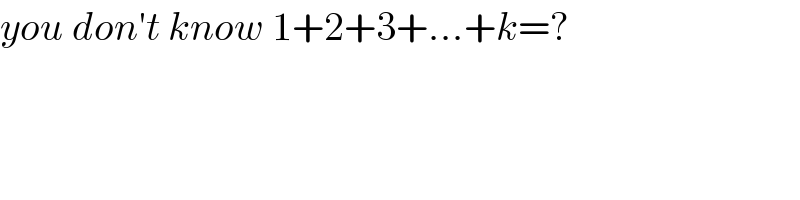
$${you}\:{don}'{t}\:{know}\:\mathrm{1}+\mathrm{2}+\mathrm{3}+…+{k}=? \\ $$

Commented by mr W last updated on 26/Jan/20

Commented by TawaTawa last updated on 26/Jan/20

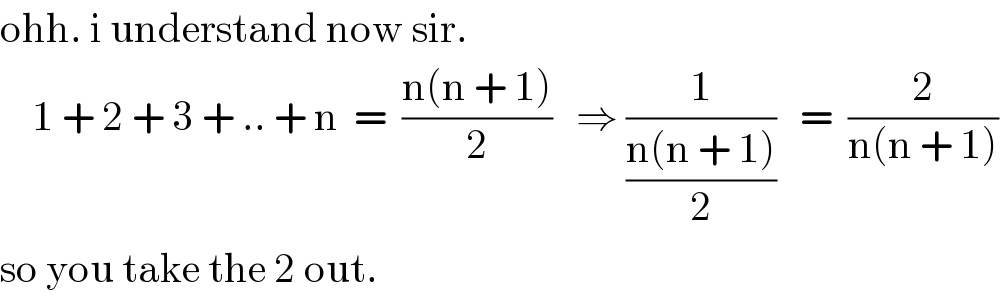
ohh. i understand now sir. 1 + 2 + 3 + .. + n = ((n(n + 1))/2) ⇒ (1/((n(n + 1))/2)) = (2/(n(n + 1))) so you take the 2 out.

$$\mathrm{ohh}.\:\mathrm{i}\:\mathrm{understand}\:\mathrm{now}\:\mathrm{sir}. \\ $$$$\:\:\:\:\mathrm{1}\:+\:\mathrm{2}\:+\:\mathrm{3}\:+\:..\:+\:\mathrm{n}\:\:=\:\:\frac{\mathrm{n}\left(\mathrm{n}\:+\:\mathrm{1}\right)}{\mathrm{2}}\:\:\:\Rightarrow\:\frac{\mathrm{1}}{\frac{\mathrm{n}\left(\mathrm{n}\:+\:\mathrm{1}\right)}{\mathrm{2}}}\:\:\:=\:\:\frac{\mathrm{2}}{\mathrm{n}\left(\mathrm{n}\:+\:\mathrm{1}\right)}\: \\ $$$$\mathrm{so}\:\mathrm{you}\:\mathrm{take}\:\mathrm{the}\:\mathrm{2}\:\mathrm{out}. \\ $$

Commented by TawaTawa last updated on 26/Jan/20

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$

Commented by john santu last updated on 27/Jan/20

1+(1/3)+(1/6)+(1/(10))+(1/(15))+(1/(21))+...=S_m consider denumerator 1,3,6,10,15,21,... T_n = ((n^2 +n)/2) = ((n(n+1))/2) Σ_(n=1 ) ^(8016) (2/(n(n+1))) = 2 Σ_(n=1) ^(8016) (1/n)−(1/(n+1)) = 2 {(1/1)−(1/(8017))} = ((16032)/(8017))

$$\mathrm{1}+\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{6}}+\frac{\mathrm{1}}{\mathrm{10}}+\frac{\mathrm{1}}{\mathrm{15}}+\frac{\mathrm{1}}{\mathrm{21}}+…=\mathrm{S}_{\mathrm{m}} \\ $$$$\mathrm{consider}\:\mathrm{denumerator} \\ $$$$\mathrm{1},\mathrm{3},\mathrm{6},\mathrm{10},\mathrm{15},\mathrm{21},… \\ $$$$\mathrm{T}_{\mathrm{n}} =\:\frac{\mathrm{n}^{\mathrm{2}} +\mathrm{n}}{\mathrm{2}}\:=\:\frac{\mathrm{n}\left(\mathrm{n}+\mathrm{1}\right)}{\mathrm{2}} \\ $$$$\underset{\mathrm{n}=\mathrm{1}\:} {\overset{\mathrm{8016}} {\sum}}\:\frac{\mathrm{2}}{\mathrm{n}\left(\mathrm{n}+\mathrm{1}\right)}\:=\:\mathrm{2}\:\underset{\mathrm{n}=\mathrm{1}} {\overset{\mathrm{8016}} {\sum}}\:\frac{\mathrm{1}}{\mathrm{n}}−\frac{\mathrm{1}}{\mathrm{n}+\mathrm{1}} \\ $$$$=\:\mathrm{2}\:\left\{\frac{\mathrm{1}}{\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{8017}}\right\}\:=\:\frac{\mathrm{16032}}{\mathrm{8017}} \\ $$$$ \\ $$

Commented by TawaTawa last updated on 27/Jan/20

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$

Facebook Tweet Pin

Sum-1-1-1-1-2-1-1-2-3-1-1-2-3-8016-

Leave a Reply Cancel reply