Sum-of-infinite-series-1-3-4-3-5-4-8-3-5-7-4-8-12-is-

Question Number 92008 by I want to learn more last updated on 04/May/20

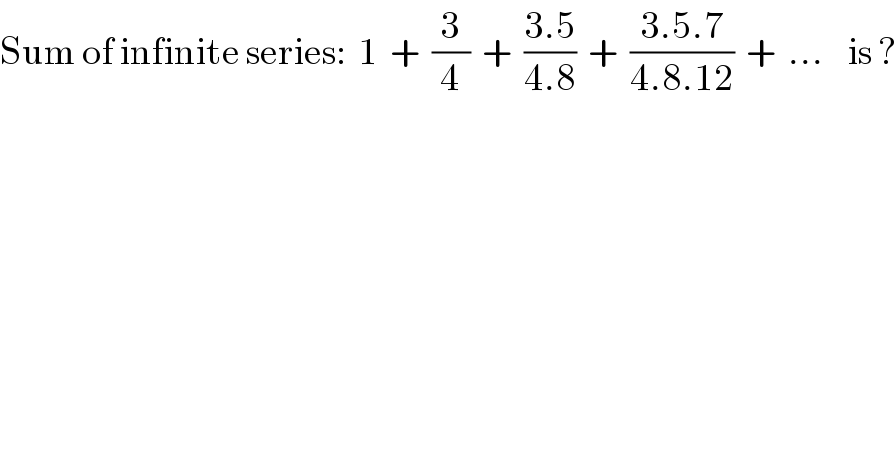
$$\mathrm{Sum}\:\mathrm{of}\:\mathrm{infinite}\:\mathrm{series}:\:\:\mathrm{1}\:\:+\:\:\frac{\mathrm{3}}{\mathrm{4}}\:\:+\:\:\frac{\mathrm{3}.\mathrm{5}}{\mathrm{4}.\mathrm{8}}\:\:+\:\:\frac{\mathrm{3}.\mathrm{5}.\mathrm{7}}{\mathrm{4}.\mathrm{8}.\mathrm{12}}\:\:+\:\:…\:\:\:\:\mathrm{is}\:? \\ $$

Commented by Prithwish Sen 1 last updated on 04/May/20

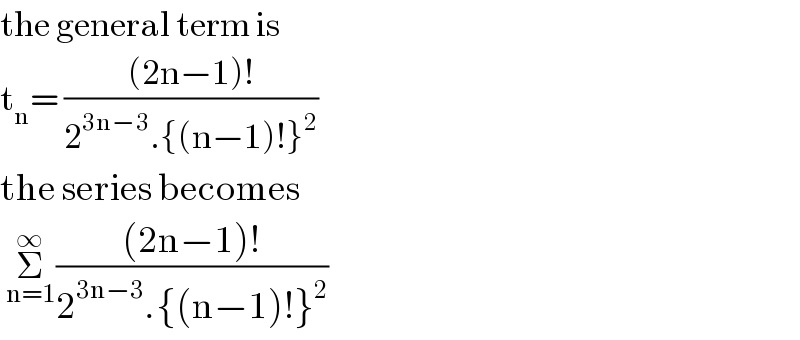
the general term is t_n = (((2n−1)!)/(2^(3n−3) .{(n−1)!}^2 )) the series becomes Σ_(n=1) ^∞ (((2n−1)!)/(2^(3n−3) .{(n−1)!}^2 ))

$$\mathrm{the}\:\mathrm{general}\:\mathrm{term}\:\mathrm{is} \\ $$$$\mathrm{t}_{\mathrm{n}} =\:\frac{\left(\mathrm{2n}−\mathrm{1}\right)!}{\mathrm{2}^{\mathrm{3n}−\mathrm{3}} .\left\{\left(\mathrm{n}−\mathrm{1}\right)!\right\}^{\mathrm{2}} }\: \\ $$$$\mathrm{the}\:\mathrm{series}\:\mathrm{becomes} \\ $$$$\:\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(\mathrm{2n}−\mathrm{1}\right)!}{\mathrm{2}^{\mathrm{3n}−\mathrm{3}} .\left\{\left(\mathrm{n}−\mathrm{1}\right)!\right\}^{\mathrm{2}} } \\ $$

Facebook Tweet Pin

Sum-of-infinite-series-1-3-4-3-5-4-8-3-5-7-4-8-12-is-

Leave a Reply Cancel reply