Menu Close

Sum-the-series-sin-2-sin-2-2-sin-2-3-sin-2-n-

Tinku Tara 0 Comments
Pin




Question Number 56602 by Tawa1 last updated on 19/Mar/19
Sum the series: sin^2 (α) + sin^2 (2α) + sin^2 (3α) + ... + sin^2 (nα)
$$\mathrm{Sum}\:\mathrm{the}\:\mathrm{series}:\:\:\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{sin}^{\mathrm{2}} \left(\alpha\right)\:+\:\mathrm{sin}^{\mathrm{2}} \left(\mathrm{2}\alpha\right)\:+\:\mathrm{sin}^{\mathrm{2}} \left(\mathrm{3}\alpha\right)\:+\:…\:+\:\mathrm{sin}^{\mathrm{2}} \left(\mathrm{n}\alpha\right) \\ $$
Commented by maxmathsup by imad last updated on 26/Mar/19
let S_n =Σ_(k=1) ^n sin^2 (kα) ⇒S_n =Σ_(k=1) ^n ((1−cos(2kα))/2) =(n/2) −(1/2)Σ_(k=1) ^n cos(2kα) but Σ_(k=1) ^n cos(2kα) =Σ_(k=0) ^n cos(2kα)−1 =Re(Σ_(k=0) ^n e^(i2kα) )−1 Σ_(k=0) ^n e^(i2kα) =Σ_(k=0) ^n (e^(i2α) )^k =((1−e^(i2(n+1)α) )/(1−e^(i2α) )) (if e^(i2α) ≠1) =((1−cos2(n+1)α−isin2(n+1)α)/(1−cos(2α)−isin(2α))) = ((2sin^2 (n+1)α −2isin((n+1)α) cos((n+1)α))/(2sin^2 α −2i sinα cosα)) =((−i sin(n+1)α{cos(n+1)α +i sin(n+1)α)/(−isinα{ cosα +isinα})) =((sin(n+1)α)/(sinα)) e^(i(n+1)α) e^(−iα) =((sin(n+1)α)/(sinα)) e^(inα) =((sin(n+1)α)/(sinα)){cos(nα)+isin(nα)} ⇒ Σ_(k=1) ^n cos(2kα) =((sin(n+1)α cos(nα))/(sinα)) −1 ⇒ S_n =(n/2) −(1/2)( ((sin(n+1)α cos(nα))/(sinα)) −1) =((n+1)/2) −((sin(n+1)α cos(nα))/(2sinα)) if e^(i2α) ≠1 .
$${let}\:{S}_{{n}} =\sum_{{k}=\mathrm{1}} ^{{n}} \:{sin}^{\mathrm{2}} \left({k}\alpha\right)\:\Rightarrow{S}_{{n}} =\sum_{{k}=\mathrm{1}} ^{{n}} \frac{\mathrm{1}−{cos}\left(\mathrm{2}{k}\alpha\right)}{\mathrm{2}} \\ $$$$=\frac{{n}}{\mathrm{2}}\:−\frac{\mathrm{1}}{\mathrm{2}}\sum_{{k}=\mathrm{1}} ^{{n}} \:{cos}\left(\mathrm{2}{k}\alpha\right)\:{but}\: \\ $$$$\sum_{{k}=\mathrm{1}} ^{{n}} \:{cos}\left(\mathrm{2}{k}\alpha\right)\:=\sum_{{k}=\mathrm{0}} ^{{n}} \:{cos}\left(\mathrm{2}{k}\alpha\right)−\mathrm{1}\:={Re}\left(\sum_{{k}=\mathrm{0}} ^{{n}} \:{e}^{{i}\mathrm{2}{k}\alpha} \right)−\mathrm{1} \\ $$$$\sum_{{k}=\mathrm{0}} ^{{n}} \:{e}^{{i}\mathrm{2}{k}\alpha} \:\:=\sum_{{k}=\mathrm{0}} ^{{n}} \:\left({e}^{{i}\mathrm{2}\alpha} \right)^{{k}} \:=\frac{\mathrm{1}−{e}^{{i}\mathrm{2}\left({n}+\mathrm{1}\right)\alpha} }{\mathrm{1}−{e}^{{i}\mathrm{2}\alpha} }\:\:\left({if}\:\:{e}^{{i}\mathrm{2}\alpha} \neq\mathrm{1}\right) \\ $$$$=\frac{\mathrm{1}−{cos}\mathrm{2}\left({n}+\mathrm{1}\right)\alpha−{isin}\mathrm{2}\left({n}+\mathrm{1}\right)\alpha}{\mathrm{1}−{cos}\left(\mathrm{2}\alpha\right)−{isin}\left(\mathrm{2}\alpha\right)}\:=\:\frac{\mathrm{2}{sin}^{\mathrm{2}} \left({n}+\mathrm{1}\right)\alpha\:−\mathrm{2}{isin}\left(\left({n}+\mathrm{1}\right)\alpha\right)\:{cos}\left(\left({n}+\mathrm{1}\right)\alpha\right)}{\mathrm{2}{sin}^{\mathrm{2}} \alpha\:−\mathrm{2}{i}\:{sin}\alpha\:{cos}\alpha} \\ $$$$=\frac{−{i}\:{sin}\left({n}+\mathrm{1}\right)\alpha\left\{{cos}\left({n}+\mathrm{1}\right)\alpha\:+{i}\:{sin}\left({n}+\mathrm{1}\right)\alpha\right.}{−{isin}\alpha\left\{\:{cos}\alpha\:+{isin}\alpha\right\}}\:=\frac{{sin}\left({n}+\mathrm{1}\right)\alpha}{{sin}\alpha}\:{e}^{{i}\left({n}+\mathrm{1}\right)\alpha} \:{e}^{−{i}\alpha} \\ $$$$=\frac{{sin}\left({n}+\mathrm{1}\right)\alpha}{{sin}\alpha}\:{e}^{{in}\alpha} \:=\frac{{sin}\left({n}+\mathrm{1}\right)\alpha}{{sin}\alpha}\left\{{cos}\left({n}\alpha\right)+{isin}\left({n}\alpha\right)\right\}\:\Rightarrow \\ $$$$\sum_{{k}=\mathrm{1}} ^{{n}} \:{cos}\left(\mathrm{2}{k}\alpha\right)\:=\frac{{sin}\left({n}+\mathrm{1}\right)\alpha\:{cos}\left({n}\alpha\right)}{{sin}\alpha}\:−\mathrm{1}\:\Rightarrow \\ $$$${S}_{{n}} =\frac{{n}}{\mathrm{2}}\:−\frac{\mathrm{1}}{\mathrm{2}}\left(\:\frac{{sin}\left({n}+\mathrm{1}\right)\alpha\:{cos}\left({n}\alpha\right)}{{sin}\alpha}\:−\mathrm{1}\right)\:=\frac{{n}+\mathrm{1}}{\mathrm{2}}\:−\frac{{sin}\left({n}+\mathrm{1}\right)\alpha\:{cos}\left({n}\alpha\right)}{\mathrm{2}{sin}\alpha} \\ $$$${if}\:{e}^{{i}\mathrm{2}\alpha} \:\neq\mathrm{1}\:. \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 19/Mar/19
T_n =sin^2 (nα) T_n =((1−cos2nα)/2) =(1/2)−(1/2)(cos2nα) T_1 =(1/2)−(1/2)(cos2α) T_2 =(1/2)−(1/2)(cos4α) T_3 =(1/2)−(1/2)(cos6α) ... ... T_n =(1/2)−(1/2)(cos2nα) S=n×(1/2)−(1/2)(cos2α+cos4α+cos6α+...+cos2nα) S=(n/2)−(p/2) p=cos2α+cos4α+cos6α+...+cos2nα 2cos2αsinα=sin3α−sinα 2cos4αsinα=sin5α−sin3α 2cos6αsinα=sin7α−sin5α ... ... 2cos2nαsinα=sin(2n+1)α−sin(2n−1)α add them 2sinα(cos2α+cos4α+..+cos2nα)=sin(2n+1)α−sinα 2sinα×p=sin(2n+1)α−sinα p=((sin(2n+1)α−sinα)/(2sinα)) So S=(n/2)−(p/2) =(n/2)−((sin(2n+1)α−sinα)/(4sinα)) pls check...
$${T}_{{n}} ={sin}^{\mathrm{2}} \left({n}\alpha\right) \\ $$$${T}_{{n}} =\frac{\mathrm{1}−{cos}\mathrm{2}{n}\alpha}{\mathrm{2}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}\left({cos}\mathrm{2}{n}\alpha\right) \\ $$$${T}_{\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}\left({cos}\mathrm{2}\alpha\right) \\ $$$${T}_{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}\left({cos}\mathrm{4}\alpha\right) \\ $$$${T}_{\mathrm{3}} =\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}\left({cos}\mathrm{6}\alpha\right) \\ $$$$… \\ $$$$… \\ $$$${T}_{{n}} =\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}\left({cos}\mathrm{2}{n}\alpha\right) \\ $$$${S}={n}×\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}\left({cos}\mathrm{2}\alpha+{cos}\mathrm{4}\alpha+{cos}\mathrm{6}\alpha+…+{cos}\mathrm{2}{n}\alpha\right) \\ $$$${S}=\frac{{n}}{\mathrm{2}}−\frac{{p}}{\mathrm{2}} \\ $$$${p}={cos}\mathrm{2}\alpha+{cos}\mathrm{4}\alpha+{cos}\mathrm{6}\alpha+…+{cos}\mathrm{2}{n}\alpha \\ $$$$\mathrm{2}{cos}\mathrm{2}\alpha{sin}\alpha={sin}\mathrm{3}\alpha−{sin}\alpha \\ $$$$\mathrm{2}{cos}\mathrm{4}\alpha{sin}\alpha={sin}\mathrm{5}\alpha−{sin}\mathrm{3}\alpha \\ $$$$\mathrm{2}{cos}\mathrm{6}\alpha{sin}\alpha={sin}\mathrm{7}\alpha−{sin}\mathrm{5}\alpha \\ $$$$… \\ $$$$… \\ $$$$\mathrm{2}{cos}\mathrm{2}{n}\alpha{sin}\alpha={sin}\left(\mathrm{2}{n}+\mathrm{1}\right)\alpha−{sin}\left(\mathrm{2}{n}−\mathrm{1}\right)\alpha \\ $$$${add}\:{them} \\ $$$$\mathrm{2}{sin}\alpha\left({cos}\mathrm{2}\alpha+{cos}\mathrm{4}\alpha+..+{cos}\mathrm{2}{n}\alpha\right)={sin}\left(\mathrm{2}{n}+\mathrm{1}\right)\alpha−{sin}\alpha \\ $$$$\mathrm{2}{sin}\alpha×{p}={sin}\left(\mathrm{2}{n}+\mathrm{1}\right)\alpha−{sin}\alpha \\ $$$${p}=\frac{{sin}\left(\mathrm{2}{n}+\mathrm{1}\right)\alpha−{sin}\alpha}{\mathrm{2}{sin}\alpha} \\ $$$${So}\:{S}=\frac{{n}}{\mathrm{2}}−\frac{{p}}{\mathrm{2}} \\ $$$$=\frac{{n}}{\mathrm{2}}−\frac{{sin}\left(\mathrm{2}{n}+\mathrm{1}\right)\alpha−{sin}\alpha}{\mathrm{4}{sin}\alpha} \\ $$$${pls}\:{check}… \\ $$$$ \\ $$
Commented by maxmathsup by imad last updated on 19/Mar/19
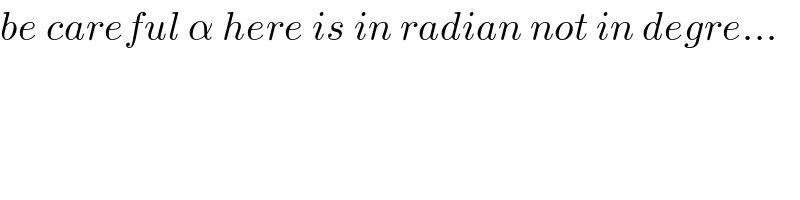
be careful α here is in radian not in degre...
$${be}\:{careful}\:\alpha\:{here}\:{is}\:{in}\:{radian}\:{not}\:{in}\:{degre}… \\ $$
Commented by Tawa1 last updated on 19/Mar/19
Thanks sir.
$$\mathrm{Thanks}\:\mathrm{sir}. \\ $$
Commented by Tawa1 last updated on 19/Mar/19
Then it will be stated that where α is in degree, can it ?
$$\mathrm{Then}\:\mathrm{it}\:\mathrm{will}\:\mathrm{be}\:\mathrm{stated}\:\mathrm{that}\:\mathrm{where}\:\:\alpha\:\mathrm{is}\:\mathrm{in}\:\mathrm{degree},\:\mathrm{can}\:\mathrm{it}\:? \\ $$
Commented by Tawa1 last updated on 19/Mar/19
I used this question sin^2 (1) + sin^2 (2) + sin^2 (3) + ... + sin^2 (89) + sin^2 (90) to form the question above sir ....
$$\mathrm{I}\:\mathrm{used}\:\mathrm{this}\:\mathrm{question}\:\:\:\mathrm{sin}^{\mathrm{2}} \left(\mathrm{1}\right)\:+\:\mathrm{sin}^{\mathrm{2}} \left(\mathrm{2}\right)\:+\:\mathrm{sin}^{\mathrm{2}} \left(\mathrm{3}\right)\:+\:…\:+\:\mathrm{sin}^{\mathrm{2}} \left(\mathrm{89}\right)\:+\:\mathrm{sin}^{\mathrm{2}} \left(\mathrm{90}\right) \\ $$$$\mathrm{to}\:\mathrm{form}\:\mathrm{the}\:\mathrm{question}\:\mathrm{above}\:\mathrm{sir}\:….\: \\ $$
Commented by Tawa1 last updated on 19/Mar/19
Correct sir. sin^2 (α) + sin^2 (2α) + sin^2 (3α) + ... + sin^2 (nα) = (n/2) − ((sin(2n + 1)α − sin(α))/(4sin(α))) where α = 1 sin^2 (1) + sin^2 (2) + sin^2 (3) + ... + sin^2 (89) + sin^2 (90) = ((90)/2) − ((sin[2(90) + 1] − sin(1))/(4 sin(1))) sin^2 (1) + sin^2 (2) + sin^2 (3) + ... + sin^2 (89) + sin^2 (90) = ((90)/2) − ((sin(180) − sin(1))/(4 sin(1))) sin^2 (1) + sin^2 (2) + sin^2 (3) + ... + sin^2 (89) + sin^2 (90) = ((90)/2) − (− (1/2)) sin^2 (1) + sin^2 (2) + sin^2 (3) + ... + sin^2 (89) + sin^2 (90) = 45 + 0.5 sin^2 (1) + sin^2 (2) + sin^2 (3) + ... + sin^2 (89) + sin^2 (90) = 45.5 Same as what you got earlier and sir mrW.
$$\mathrm{Correct}\:\mathrm{sir}. \\ $$$$ \\ $$$$\:\mathrm{sin}^{\mathrm{2}} \left(\alpha\right)\:+\:\mathrm{sin}^{\mathrm{2}} \left(\mathrm{2}\alpha\right)\:+\:\mathrm{sin}^{\mathrm{2}} \left(\mathrm{3}\alpha\right)\:+\:…\:+\:\mathrm{sin}^{\mathrm{2}} \left(\mathrm{n}\alpha\right)\:\:=\:\:\frac{\mathrm{n}}{\mathrm{2}}\:−\:\frac{\mathrm{sin}\left(\mathrm{2n}\:+\:\mathrm{1}\right)\alpha\:−\:\mathrm{sin}\left(\alpha\right)}{\mathrm{4sin}\left(\alpha\right)} \\ $$$$\mathrm{where}\:\:\alpha\:\:=\:\:\mathrm{1} \\ $$$$\:\mathrm{sin}^{\mathrm{2}} \left(\mathrm{1}\right)\:+\:\mathrm{sin}^{\mathrm{2}} \left(\mathrm{2}\right)\:+\:\mathrm{sin}^{\mathrm{2}} \left(\mathrm{3}\right)\:+\:…\:+\:\mathrm{sin}^{\mathrm{2}} \left(\mathrm{89}\right)\:+\:\mathrm{sin}^{\mathrm{2}} \left(\mathrm{90}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\:\frac{\mathrm{90}}{\mathrm{2}}\:−\:\frac{\mathrm{sin}\left[\mathrm{2}\left(\mathrm{90}\right)\:+\:\mathrm{1}\right]\:−\:\mathrm{sin}\left(\mathrm{1}\right)}{\mathrm{4}\:\mathrm{sin}\left(\mathrm{1}\right)} \\ $$$$\:\mathrm{sin}^{\mathrm{2}} \left(\mathrm{1}\right)\:+\:\mathrm{sin}^{\mathrm{2}} \left(\mathrm{2}\right)\:+\:\mathrm{sin}^{\mathrm{2}} \left(\mathrm{3}\right)\:+\:…\:+\:\mathrm{sin}^{\mathrm{2}} \left(\mathrm{89}\right)\:+\:\mathrm{sin}^{\mathrm{2}} \left(\mathrm{90}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\:\frac{\mathrm{90}}{\mathrm{2}}\:−\:\frac{\mathrm{sin}\left(\mathrm{180}\right)\:−\:\mathrm{sin}\left(\mathrm{1}\right)}{\mathrm{4}\:\mathrm{sin}\left(\mathrm{1}\right)} \\ $$$$\:\mathrm{sin}^{\mathrm{2}} \left(\mathrm{1}\right)\:+\:\mathrm{sin}^{\mathrm{2}} \left(\mathrm{2}\right)\:+\:\mathrm{sin}^{\mathrm{2}} \left(\mathrm{3}\right)\:+\:…\:+\:\mathrm{sin}^{\mathrm{2}} \left(\mathrm{89}\right)\:+\:\mathrm{sin}^{\mathrm{2}} \left(\mathrm{90}\right)\:\:=\:\:\frac{\mathrm{90}}{\mathrm{2}}\:−\:\left(−\:\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$$\:\mathrm{sin}^{\mathrm{2}} \left(\mathrm{1}\right)\:+\:\mathrm{sin}^{\mathrm{2}} \left(\mathrm{2}\right)\:+\:\mathrm{sin}^{\mathrm{2}} \left(\mathrm{3}\right)\:+\:…\:+\:\mathrm{sin}^{\mathrm{2}} \left(\mathrm{89}\right)\:+\:\mathrm{sin}^{\mathrm{2}} \left(\mathrm{90}\right)\:\:=\:\:\mathrm{45}\:+\:\mathrm{0}.\mathrm{5} \\ $$$$\:\mathrm{sin}^{\mathrm{2}} \left(\mathrm{1}\right)\:+\:\mathrm{sin}^{\mathrm{2}} \left(\mathrm{2}\right)\:+\:\mathrm{sin}^{\mathrm{2}} \left(\mathrm{3}\right)\:+\:…\:+\:\mathrm{sin}^{\mathrm{2}} \left(\mathrm{89}\right)\:+\:\mathrm{sin}^{\mathrm{2}} \left(\mathrm{90}\right)\:\:=\:\:\mathrm{45}.\mathrm{5} \\ $$$$ \\ $$$$\mathrm{Same}\:\mathrm{as}\:\mathrm{what}\:\mathrm{you}\:\mathrm{got}\:\mathrm{earlier}\:\mathrm{and}\:\mathrm{sir}\:\:\mathrm{mrW}.\: \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *