Question Number 172687 by Rasheed.Sindhi last updated on 30/Jun/22

$$\mathrm{Sum}\:\mathrm{to}\:\mathrm{n}\:\mathrm{terms}: \\ $$$$\mathrm{7}+\mathrm{77}+\mathrm{777}+… \\ $$
Commented by mr W last updated on 30/Jun/22
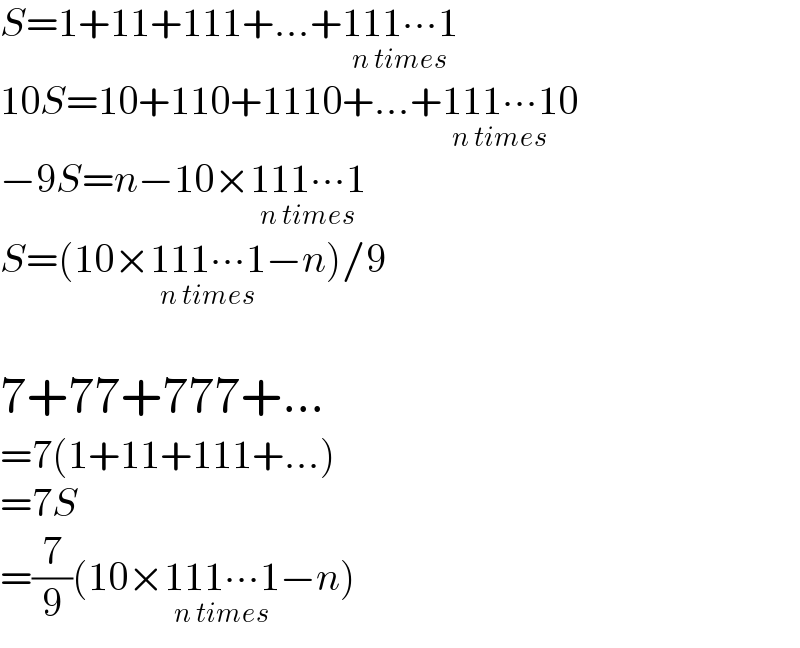
$${S}=\mathrm{1}+\mathrm{11}+\mathrm{111}+…+\underset{{n}\:{times}} {\mathrm{111}\centerdot\centerdot\centerdot\mathrm{1}} \\ $$$$\mathrm{10}{S}=\mathrm{10}+\mathrm{110}+\mathrm{1110}+…+\underset{{n}\:{times}} {\mathrm{111}\centerdot\centerdot\centerdot\mathrm{1}0} \\ $$$$−\mathrm{9}{S}={n}−\mathrm{10}×\underset{{n}\:{times}} {\mathrm{111}\centerdot\centerdot\centerdot\mathrm{1}} \\ $$$${S}=\left(\mathrm{10}×\underset{{n}\:{times}} {\mathrm{111}\centerdot\centerdot\centerdot\mathrm{1}}−{n}\right)/\mathrm{9} \\ $$$$ \\ $$$$\mathrm{7}+\mathrm{77}+\mathrm{777}+… \\ $$$$=\mathrm{7}\left(\mathrm{1}+\mathrm{11}+\mathrm{111}+…\right) \\ $$$$=\mathrm{7}{S} \\ $$$$=\frac{\mathrm{7}}{\mathrm{9}}\left(\mathrm{10}×\underset{{n}\:{times}} {\mathrm{111}\centerdot\centerdot\centerdot\mathrm{1}}−{n}\right) \\ $$
Commented by Rasheed.Sindhi last updated on 30/Jun/22

$$\mathcal{T}{han}\mathcal{X}\:{sir}! \\ $$
Commented by Tawa11 last updated on 01/Jul/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$
Answered by som(math1967) last updated on 30/Jun/22
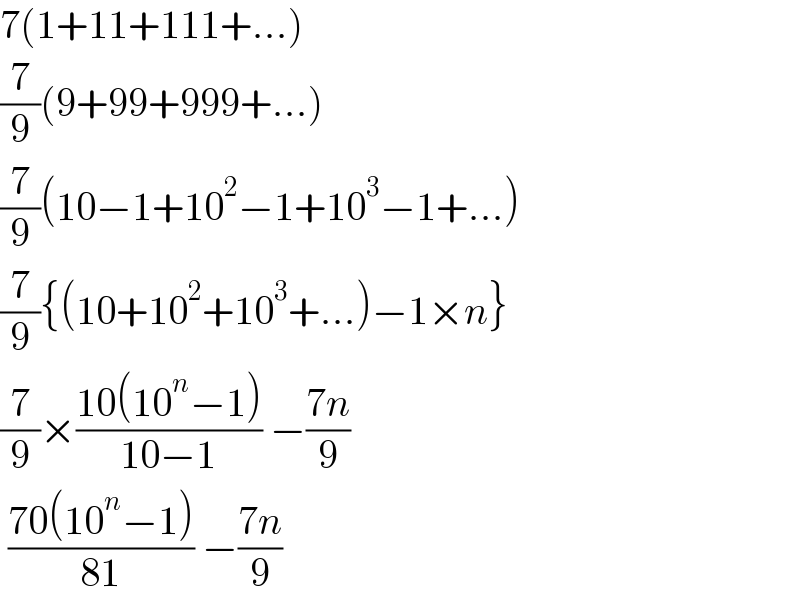
$$\mathrm{7}\left(\mathrm{1}+\mathrm{11}+\mathrm{111}+…\right) \\ $$$$\frac{\mathrm{7}}{\mathrm{9}}\left(\mathrm{9}+\mathrm{99}+\mathrm{999}+…\right) \\ $$$$\frac{\mathrm{7}}{\mathrm{9}}\left(\mathrm{10}−\mathrm{1}+\mathrm{10}^{\mathrm{2}} −\mathrm{1}+\mathrm{10}^{\mathrm{3}} −\mathrm{1}+…\right) \\ $$$$\frac{\mathrm{7}}{\mathrm{9}}\left\{\left(\mathrm{10}+\mathrm{10}^{\mathrm{2}} +\mathrm{10}^{\mathrm{3}} +…\right)−\mathrm{1}×{n}\right\} \\ $$$$\frac{\mathrm{7}}{\mathrm{9}}×\frac{\mathrm{10}\left(\mathrm{10}^{{n}} −\mathrm{1}\right)}{\mathrm{10}−\mathrm{1}}\:−\frac{\mathrm{7}{n}}{\mathrm{9}} \\ $$$$\:\frac{\mathrm{70}\left(\mathrm{10}^{{n}} −\mathrm{1}\right)}{\mathrm{81}}\:−\frac{\mathrm{7}{n}}{\mathrm{9}} \\ $$
Commented by Rasheed.Sindhi last updated on 30/Jun/22

$$\mathbb{T}\mathrm{han}\Bbbk\mathrm{s}\:\mathrm{sir}! \\ $$
Commented by Tawa11 last updated on 01/Jul/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$
Commented by peter frank last updated on 03/Jul/22

$$\mathrm{thank}\:\mathrm{you} \\ $$
