Question Number 149598 by naka3546 last updated on 06/Aug/21
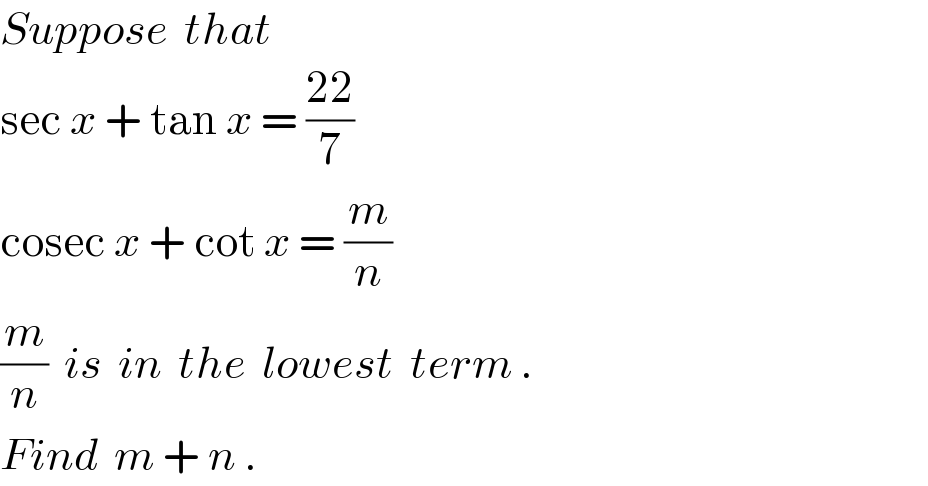
$${Suppose}\:\:{that}\:\: \\ $$$$\mathrm{sec}\:{x}\:+\:\mathrm{tan}\:{x}\:=\:\frac{\mathrm{22}}{\mathrm{7}} \\ $$$$\mathrm{cosec}\:{x}\:+\:\mathrm{cot}\:{x}\:=\:\frac{{m}}{{n}} \\ $$$$\frac{{m}}{{n}}\:\:{is}\:\:{in}\:\:{the}\:\:{lowest}\:\:{term}\:. \\ $$$${Find}\:\:{m}\:+\:{n}\:. \\ $$
Answered by iloveisrael last updated on 06/Aug/21
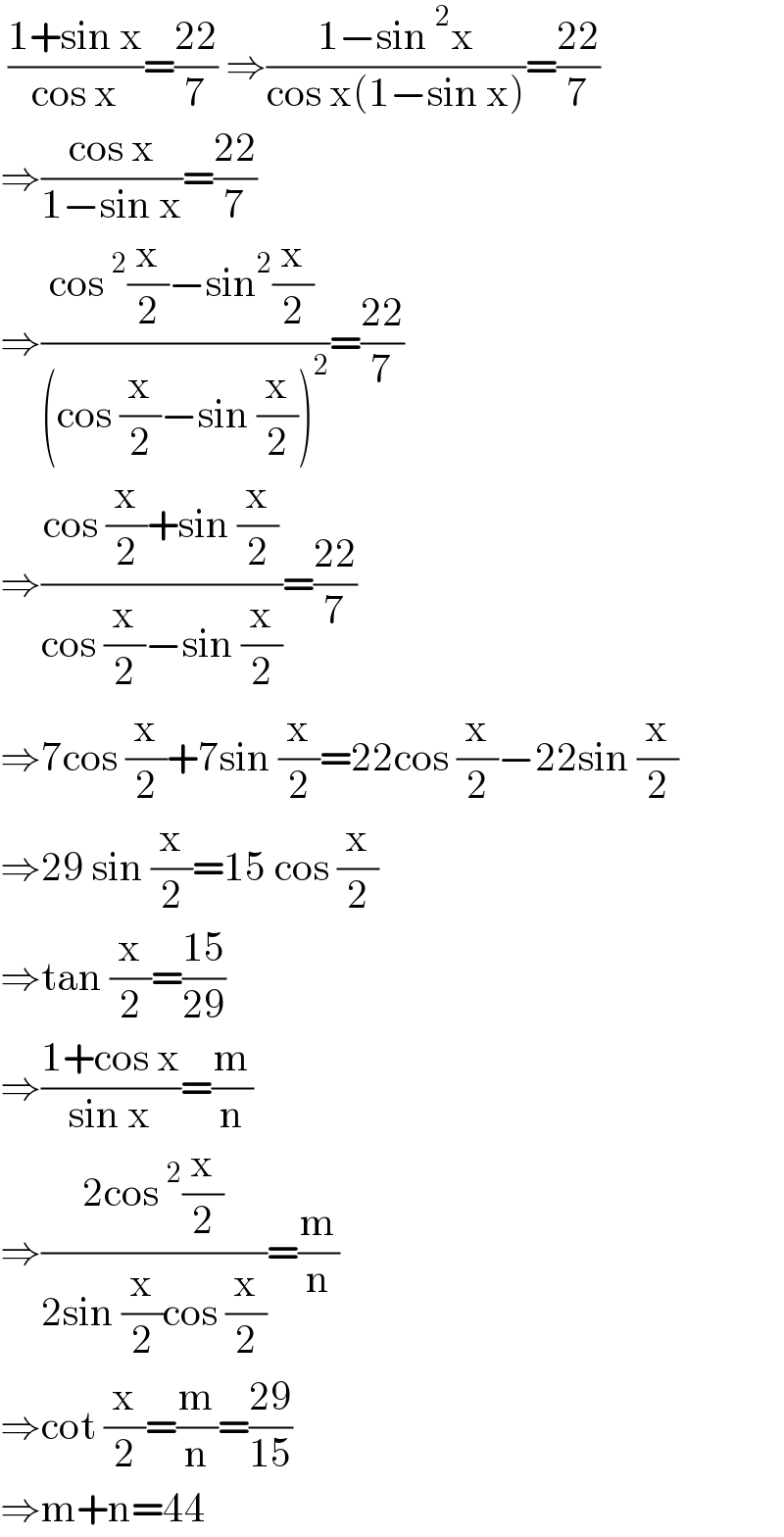
$$\:\frac{\mathrm{1}+\mathrm{sin}\:\mathrm{x}}{\mathrm{cos}\:\mathrm{x}}=\frac{\mathrm{22}}{\mathrm{7}}\:\Rightarrow\frac{\mathrm{1}−\mathrm{sin}\:^{\mathrm{2}} \mathrm{x}}{\mathrm{cos}\:\mathrm{x}\left(\mathrm{1}−\mathrm{sin}\:\mathrm{x}\right)}=\frac{\mathrm{22}}{\mathrm{7}} \\ $$$$\Rightarrow\frac{\mathrm{cos}\:\mathrm{x}}{\mathrm{1}−\mathrm{sin}\:\mathrm{x}}=\frac{\mathrm{22}}{\mathrm{7}} \\ $$$$\Rightarrow\frac{\mathrm{cos}\:^{\mathrm{2}} \frac{\mathrm{x}}{\mathrm{2}}−\mathrm{sin}^{\mathrm{2}} \frac{\mathrm{x}}{\mathrm{2}}\:}{\left(\mathrm{cos}\:\frac{\mathrm{x}}{\mathrm{2}}−\mathrm{sin}\:\frac{\mathrm{x}}{\mathrm{2}}\right)^{\mathrm{2}} }=\frac{\mathrm{22}}{\mathrm{7}} \\ $$$$\Rightarrow\frac{\mathrm{cos}\:\frac{\mathrm{x}}{\mathrm{2}}+\mathrm{sin}\:\frac{\mathrm{x}}{\mathrm{2}}}{\mathrm{cos}\:\frac{\mathrm{x}}{\mathrm{2}}−\mathrm{sin}\:\frac{\mathrm{x}}{\mathrm{2}}}=\frac{\mathrm{22}}{\mathrm{7}} \\ $$$$\Rightarrow\mathrm{7cos}\:\frac{\mathrm{x}}{\mathrm{2}}+\mathrm{7sin}\:\frac{\mathrm{x}}{\mathrm{2}}=\mathrm{22cos}\:\frac{\mathrm{x}}{\mathrm{2}}−\mathrm{22sin}\:\frac{\mathrm{x}}{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{29}\:\mathrm{sin}\:\frac{\mathrm{x}}{\mathrm{2}}=\mathrm{15}\:\mathrm{cos}\:\frac{\mathrm{x}}{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{tan}\:\frac{\mathrm{x}}{\mathrm{2}}=\frac{\mathrm{15}}{\mathrm{29}} \\ $$$$\Rightarrow\frac{\mathrm{1}+\mathrm{cos}\:\mathrm{x}}{\mathrm{sin}\:\mathrm{x}}=\frac{\mathrm{m}}{\mathrm{n}} \\ $$$$\Rightarrow\frac{\mathrm{2cos}\:^{\mathrm{2}} \frac{\mathrm{x}}{\mathrm{2}}}{\mathrm{2sin}\:\frac{\mathrm{x}}{\mathrm{2}}\mathrm{cos}\:\frac{\mathrm{x}}{\mathrm{2}}}=\frac{\mathrm{m}}{\mathrm{n}} \\ $$$$\Rightarrow\mathrm{cot}\:\frac{\mathrm{x}}{\mathrm{2}}=\frac{\mathrm{m}}{\mathrm{n}}=\frac{\mathrm{29}}{\mathrm{15}} \\ $$$$\Rightarrow\mathrm{m}+\mathrm{n}=\mathrm{44} \\ $$
Answered by nimnim last updated on 06/Aug/21

$$\:\:\:\:\:\:\:\:\:{secx}+{tanx}=\frac{\mathrm{22}}{\mathrm{7}}…..\left({i}\right) \\ $$$$\Rightarrow\:\:\:{secx}−{tanx}=\frac{\mathrm{7}}{\mathrm{22}}….\left({ii}\right) \\ $$$$\left({i}\right)+\left({ii}\right)\Rightarrow\mathrm{2}{secx}=\left(\frac{\mathrm{22}}{\mathrm{7}}+\frac{\mathrm{7}}{\mathrm{22}}\right)\Rightarrow{secx}=\frac{\mathrm{533}}{\mathrm{308}} \\ $$$$\left({i}\right)−\left({ii}\right)=\mathrm{2}{tanx}=\left(\frac{\mathrm{22}}{\mathrm{7}}−\frac{\mathrm{7}}{\mathrm{22}}\right)\Rightarrow{tanx}=\frac{\mathrm{435}}{\mathrm{308}}\: \\ $$$$\:\:\:\:\:\:{cosecx}=\frac{{secx}}{{tanx}}=\frac{\mathrm{533}}{\mathrm{435}}\:\:{and}\:\:{cotx}=\frac{\mathrm{308}}{\mathrm{435}} \\ $$$$\:\:\:\:\:\:\Rightarrow\:{cosecx}+{cotx}=\frac{\mathrm{533}}{\mathrm{435}}+\frac{\mathrm{308}}{\mathrm{435}}=\frac{{m}}{{n}} \\ $$$$\:\:\:\:\:\:\:\:\Rightarrow\frac{\mathrm{841}}{\mathrm{435}}=\frac{{m}}{{n}}\Rightarrow\frac{\mathrm{29}}{\mathrm{15}}=\frac{{m}}{{n}} \\ $$$$\:\:\:\:\therefore\:{m}+{n}=\mathrm{29}+\mathrm{15}=\mathrm{44}\bigstar \\ $$
