Question Number 157584 by MathsFan last updated on 24/Oct/21

$${suppose}\: \\ $$$${the}\:{ratio}\:{of}\:{Jim}\:{to}\:{Rohn}\:{is}\:\mathrm{2}:\mathrm{1} \\ $$$$\:{and}\:{the}\:{ratio}\:{of}\:{Rohn}\:{to}\:{Bill}\:{is} \\ $$$$\:\mathrm{3}:\mathrm{4},\:{how}\:{do}\:{i}\:{find}\:{for}\:{the}\:{ratio} \\ $$$${of}\:{Jim}\:{to}\:{Bill}…..??? \\ $$
Answered by peter frank last updated on 25/Oct/21
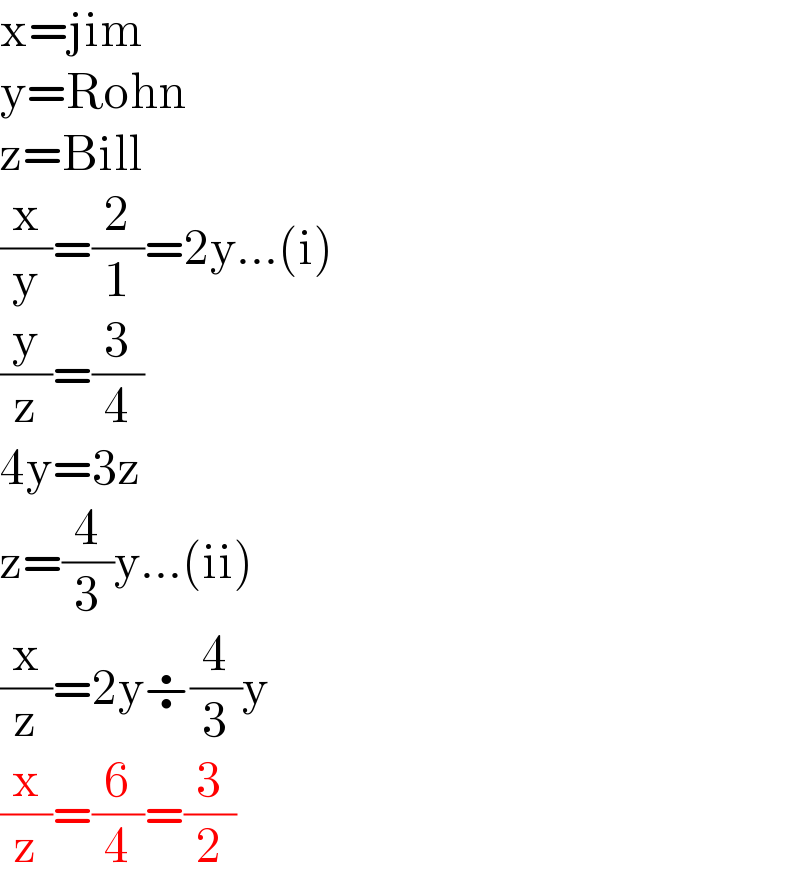
$$\mathrm{x}=\mathrm{jim} \\ $$$$\mathrm{y}=\mathrm{Rohn} \\ $$$$\mathrm{z}=\mathrm{Bill} \\ $$$$\frac{\mathrm{x}}{\mathrm{y}}=\frac{\mathrm{2}}{\mathrm{1}}=\mathrm{2y}…\left(\mathrm{i}\right) \\ $$$$\frac{\mathrm{y}}{\mathrm{z}}=\frac{\mathrm{3}}{\mathrm{4}} \\ $$$$\mathrm{4y}=\mathrm{3z} \\ $$$$\mathrm{z}=\frac{\mathrm{4}}{\mathrm{3}}\mathrm{y}…\left(\mathrm{ii}\right) \\ $$$$\frac{\mathrm{x}}{\mathrm{z}}=\mathrm{2y}\boldsymbol{\div}\frac{\mathrm{4}}{\mathrm{3}}\mathrm{y} \\ $$$$\frac{\mathrm{x}}{\mathrm{z}}=\frac{\mathrm{6}}{\mathrm{4}}=\frac{\mathrm{3}}{\mathrm{2}} \\ $$
Commented by MathsFan last updated on 25/Oct/21

$${thanks} \\ $$
Answered by Rasheed.Sindhi last updated on 25/Oct/21
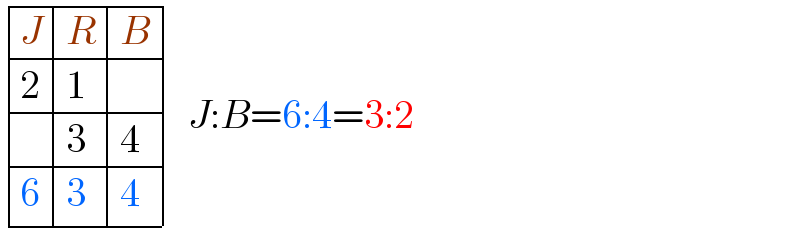
$$\begin{array}{|c|c|c|c|}{{J}}&\hline{{R}}&\hline{{B}}\\{\mathrm{2}}&\hline{\mathrm{1}}&\hline{}\\{}&\hline{\mathrm{3}}&\hline{\mathrm{4}}\\{\mathrm{6}}&\hline{\mathrm{3}}&\hline{\mathrm{4}}\\\hline\end{array}\:\:{J}:{B}=\mathrm{6}:\mathrm{4}=\mathrm{3}:\mathrm{2} \\ $$
Commented by MathsFan last updated on 25/Oct/21
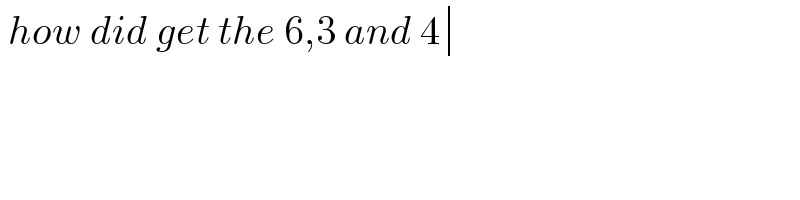
$$\:{how}\:{did}\:{get}\:{the}\:\mathrm{6},\mathrm{3}\:{and}\:\mathrm{4}\begin{array}{|c|c|c|}\\\\\\\hline\end{array} \\ $$
Commented by Rasheed.Sindhi last updated on 25/Oct/21

$$\begin{array}{|c|c|c|c|c|c|}{{J}}&\hline{{R}}&\hline{{B}}&\hline{}\\{\mathrm{2}}&\hline{\mathrm{1}^{\bigstar} }&\hline{}&\hline{}\\{}&\hline{\mathrm{3}^{\bigstar} }&\hline{\mathrm{4}}&\hline{}\\{\mathrm{6}}&\hline{\mathrm{3}^{\ast} }&\hline{}&\hline{\underset{\underset{\mathrm{3}^{\ast} ={LCM}\left(\mathrm{1}^{\bigstar} ,\mathrm{3}^{\bigstar} \right)} {\left({to}\:{meet}\:\mathrm{3}\:{in}\:\mathrm{2}{nd}\:{position}\right)}} {{mutiplied}\:{by}\:\mathrm{3}\:{to}\:\mathrm{1}{st}\:{ratio}}}\\{}&\hline{\mathrm{3}}&\hline{\mathrm{4}}&\hline{\underset{\left({to}\:{meet}\:\mathrm{3}\left({LCM}\left(\mathrm{1}^{\bigstar} ,\mathrm{3}^{\bigstar} \right)\right)\:{in}\:\mathrm{1}{st}\:\:{position}\right)} {{mutiplied}\:{by}\:\mathrm{1}\:{to}\:\mathrm{2}{nd}\:{ratio}}}\\{\mathrm{6}}&\hline{\mathrm{3}}&\hline{\mathrm{4}}&\hline{}\\\hline\end{array}\:\:{J}:{B}=\mathrm{6}:\mathrm{4}=\mathrm{3}:\mathrm{2} \\ $$$$\:\:\:\:\:\:\mathrm{OR} \\ $$$$\:\begin{array}{|c|c|c|c|}{{J}}&\hline{{R}}&\hline{{B}}\\{{a}}&\hline{{b}}&\hline{}\\{}&\hline{{c}}&\hline{{d}}\\{{ac}}&\hline{{bc}}&\hline{{bd}}\\\hline\end{array}\:\:{J}:{B}={ac}:{bd} \\ $$
Commented by MathsFan last updated on 25/Oct/21

$${interesting} \\ $$$${thank}\:{you} \\ $$
Answered by mr W last updated on 25/Oct/21
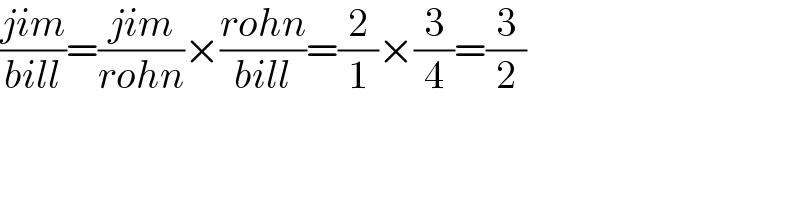
$$\frac{{jim}}{{bill}}=\frac{{jim}}{{rohn}}×\frac{{rohn}}{{bill}}=\frac{\mathrm{2}}{\mathrm{1}}×\frac{\mathrm{3}}{\mathrm{4}}=\frac{\mathrm{3}}{\mathrm{2}} \\ $$
Commented by MathsFan last updated on 25/Oct/21

$${im}\:{grateful}\:{sir} \\ $$
