Question Number 125977 by liberty last updated on 16/Dec/20

$$\:{Suppose}\:{you}\:{put}\:\$\mathrm{3000}\:{in}\:{a}\:{savings}\:{account} \\ $$$${with}\:{a}\:\mathrm{5\%}\:{annual}\:{interesrate}\:,\:{compounded} \\ $$$${continously}\:.\:{How}\:{long}\:{would}\:{it}\:{take}\:{for} \\ $$$${your}\:{money}\:{tl}\:{double}\:?\: \\ $$
Answered by bramlexs22 last updated on 16/Dec/20
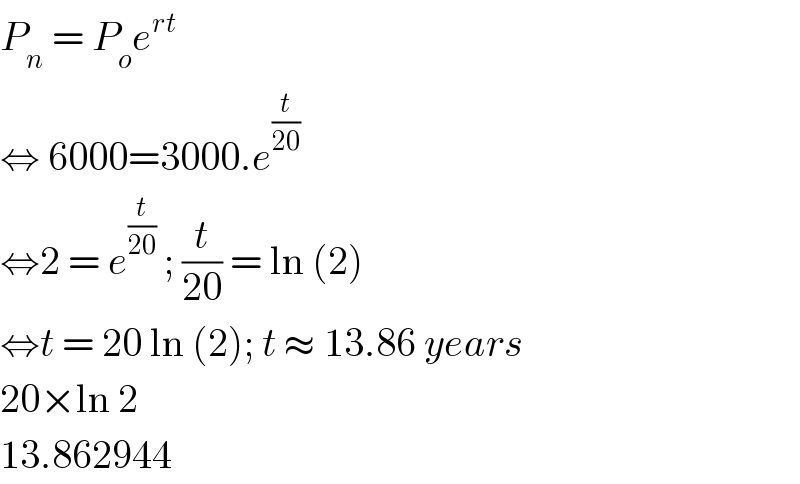
$${P}_{{n}} \:=\:{P}_{{o}} {e}^{{rt}} \\ $$$$\Leftrightarrow\:\mathrm{6000}=\mathrm{3000}.{e}^{\frac{{t}}{\mathrm{20}}} \\ $$$$\Leftrightarrow\mathrm{2}\:=\:{e}^{\frac{{t}}{\mathrm{20}}} \:;\:\frac{{t}}{\mathrm{20}}\:=\:\mathrm{ln}\:\left(\mathrm{2}\right) \\ $$$$\Leftrightarrow{t}\:=\:\mathrm{20}\:\mathrm{ln}\:\left(\mathrm{2}\right);\:{t}\:\approx\:\mathrm{13}.\mathrm{86}\:{years} \\ $$$$\mathrm{20}×\mathrm{ln}\:\mathrm{2} \\ $$$$\mathrm{13}.\mathrm{862944} \\ $$
