Question Number 93683 by i jagooll last updated on 14/May/20
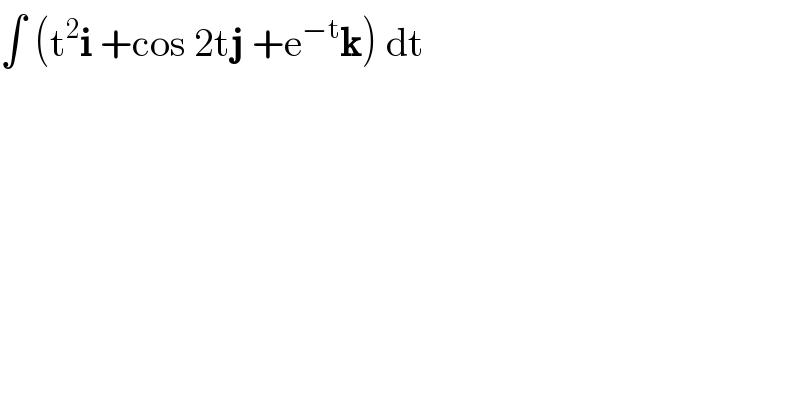
$$\int\:\left(\mathrm{t}^{\mathrm{2}} \boldsymbol{\mathrm{i}}\:+\mathrm{cos}\:\mathrm{2t}\boldsymbol{\mathrm{j}}\:+\mathrm{e}^{−\mathrm{t}} \boldsymbol{\mathrm{k}}\right)\:\mathrm{dt}\: \\ $$
Answered by john santu last updated on 14/May/20
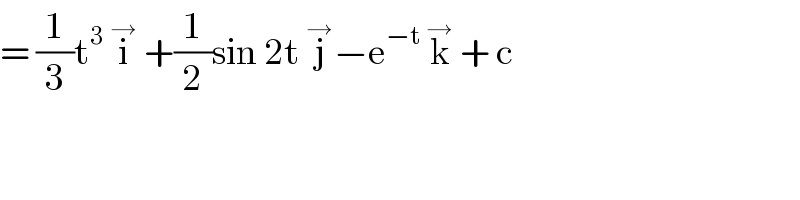
$$=\:\frac{\mathrm{1}}{\mathrm{3}}\mathrm{t}^{\mathrm{3}} \:\overset{\rightarrow} {\mathrm{i}}\:+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\:\mathrm{2t}\:\overset{\rightarrow} {\mathrm{j}}−\mathrm{e}^{−\mathrm{t}} \:\overset{\rightarrow} {\mathrm{k}}\:+\:\mathrm{c}\: \\ $$
