Question Number 45373 by arvinddayama01@gmail.com last updated on 12/Oct/18

$$\int\frac{\mathrm{t}^{\mathrm{3}} }{\mathrm{1}+\mathrm{t}}\mathrm{dt}=? \\ $$
Commented by maxmathsup by imad last updated on 12/Oct/18
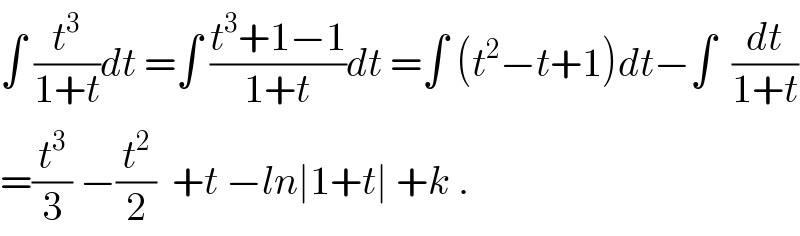
$$\int\:\frac{{t}^{\mathrm{3}} }{\mathrm{1}+{t}}{dt}\:=\int\:\frac{{t}^{\mathrm{3}} +\mathrm{1}−\mathrm{1}}{\mathrm{1}+{t}}{dt}\:=\int\:\left({t}^{\mathrm{2}} −{t}+\mathrm{1}\right){dt}−\int\:\:\frac{{dt}}{\mathrm{1}+{t}} \\ $$$$=\frac{{t}^{\mathrm{3}} }{\mathrm{3}}\:−\frac{{t}^{\mathrm{2}} }{\mathrm{2}}\:\:+{t}\:−{ln}\mid\mathrm{1}+{t}\mid\:+{k}\:. \\ $$
Answered by ajfour last updated on 12/Oct/18

$$\int\frac{\left(\mathrm{1}+{t}\right)\left(\mathrm{1}−{t}+{t}^{\mathrm{2}} \right)}{\mathrm{1}+{t}}{dt}−\int\frac{{dt}}{\mathrm{1}+{t}} \\ $$$$=\:{t}−\frac{{t}^{\mathrm{2}} }{\mathrm{2}}+\frac{{t}^{\mathrm{3}} }{\mathrm{3}}−\mathrm{ln}\:\mid\mathrm{1}+{t}\mid+{c}\:. \\ $$
