Menu Close

t-3-2t-t-1-t-t-2-1-dt-

Tinku Tara 0 Comments
Pin




Question Number 92869 by phenom last updated on 09/May/20
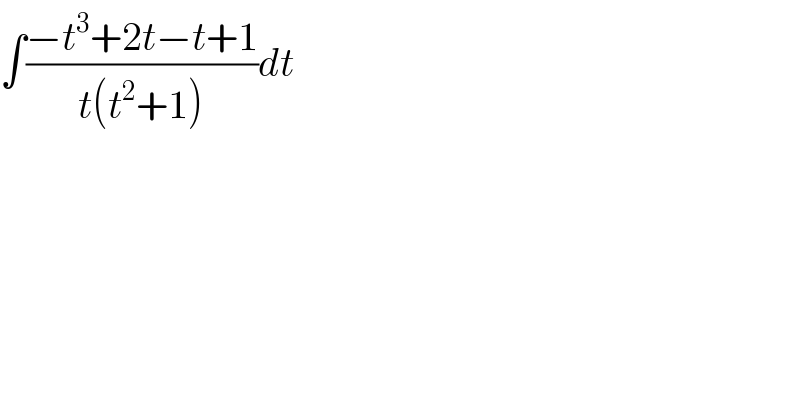
∫((−t^3 +2t−t+1)/(t(t^2 +1)))dt
$$\int\frac{−{t}^{\mathrm{3}} +\mathrm{2}{t}−{t}+\mathrm{1}}{{t}\left({t}^{\mathrm{2}} +\mathrm{1}\right)}{dt} \\ $$
Commented by phenom last updated on 09/May/20
yh it is 2t^2 sorry
$${yh}\:{it}\:{is}\:\mathrm{2}{t}^{\mathrm{2}} \:{sorry} \\ $$
Commented by phenom last updated on 09/May/20
yh it is 2t^2 sorry
$${yh}\:{it}\:{is}\:\mathrm{2}{t}^{\mathrm{2}} \:{sorry} \\ $$
Commented by john santu last updated on 09/May/20
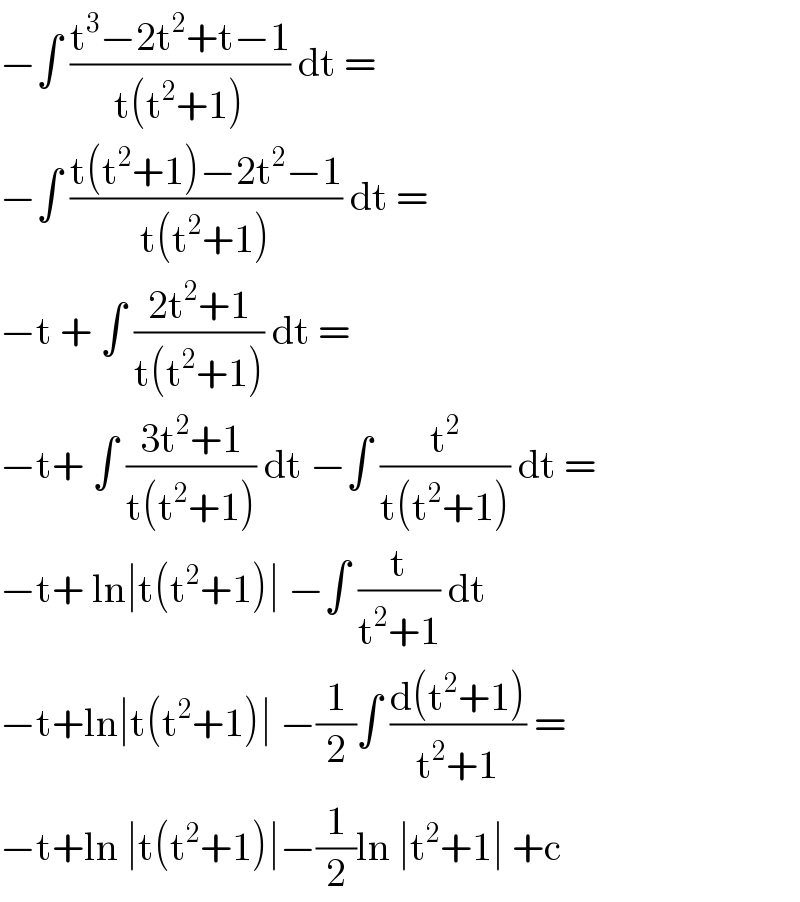
−∫ ((t^3 −2t^2 +t−1)/(t(t^2 +1))) dt = −∫ ((t(t^2 +1)−2t^2 −1)/(t(t^2 +1))) dt = −t + ∫ ((2t^2 +1)/(t(t^2 +1))) dt = −t+ ∫ ((3t^2 +1)/(t(t^2 +1))) dt −∫ (t^2 /(t(t^2 +1))) dt = −t+ ln∣t(t^2 +1)∣ −∫ (t/(t^2 +1)) dt −t+ln∣t(t^2 +1)∣ −(1/2)∫ ((d(t^2 +1))/(t^2 +1)) = −t+ln ∣t(t^2 +1)∣−(1/2)ln ∣t^2 +1∣ +c
$$−\int\:\frac{\mathrm{t}^{\mathrm{3}} −\mathrm{2t}^{\mathrm{2}} +\mathrm{t}−\mathrm{1}}{\mathrm{t}\left(\mathrm{t}^{\mathrm{2}} +\mathrm{1}\right)}\:\mathrm{dt}\:=\: \\ $$$$−\int\:\frac{\mathrm{t}\left(\mathrm{t}^{\mathrm{2}} +\mathrm{1}\right)−\mathrm{2t}^{\mathrm{2}} −\mathrm{1}}{\mathrm{t}\left(\mathrm{t}^{\mathrm{2}} +\mathrm{1}\right)}\:\mathrm{dt}\:= \\ $$$$−\mathrm{t}\:+\:\int\:\frac{\mathrm{2t}^{\mathrm{2}} +\mathrm{1}}{\mathrm{t}\left(\mathrm{t}^{\mathrm{2}} +\mathrm{1}\right)}\:\mathrm{dt}\:=\: \\ $$$$−\mathrm{t}+\:\int\:\frac{\mathrm{3t}^{\mathrm{2}} +\mathrm{1}}{\mathrm{t}\left(\mathrm{t}^{\mathrm{2}} +\mathrm{1}\right)}\:\mathrm{dt}\:−\int\:\frac{\mathrm{t}^{\mathrm{2}} }{\mathrm{t}\left(\mathrm{t}^{\mathrm{2}} +\mathrm{1}\right)}\:\mathrm{dt}\:= \\ $$$$−\mathrm{t}+\:\mathrm{ln}\mid\mathrm{t}\left(\mathrm{t}^{\mathrm{2}} +\mathrm{1}\right)\mid\:−\int\:\frac{\mathrm{t}}{\mathrm{t}^{\mathrm{2}} +\mathrm{1}}\:\mathrm{dt}\: \\ $$$$−\mathrm{t}+\mathrm{ln}\mid\mathrm{t}\left(\mathrm{t}^{\mathrm{2}} +\mathrm{1}\right)\mid\:−\frac{\mathrm{1}}{\mathrm{2}}\int\:\frac{\mathrm{d}\left(\mathrm{t}^{\mathrm{2}} +\mathrm{1}\right)}{\mathrm{t}^{\mathrm{2}} +\mathrm{1}}\:= \\ $$$$−\mathrm{t}+\mathrm{ln}\:\mid\mathrm{t}\left(\mathrm{t}^{\mathrm{2}} +\mathrm{1}\right)\mid−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\mid\mathrm{t}^{\mathrm{2}} +\mathrm{1}\mid\:+\mathrm{c}\: \\ $$
Commented by s.ayeni14@yahoo.com last updated on 09/May/20
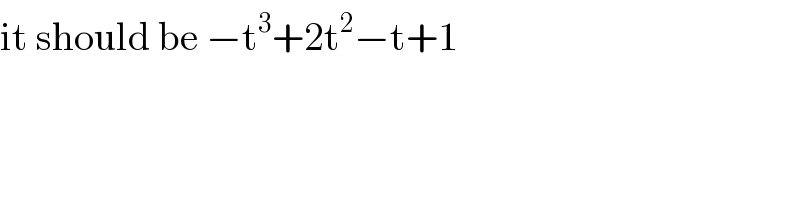
it should be −t^3 +2t^2 −t+1
$$\mathrm{it}\:\mathrm{should}\:\mathrm{be}\:−\mathrm{t}^{\mathrm{3}} +\mathrm{2t}^{\mathrm{2}} −\mathrm{t}+\mathrm{1} \\ $$
Commented by phenom last updated on 09/May/20
thanks
$$ \\ $$$${thanks} \\ $$
Commented by s.ayeni14@yahoo.com last updated on 09/May/20
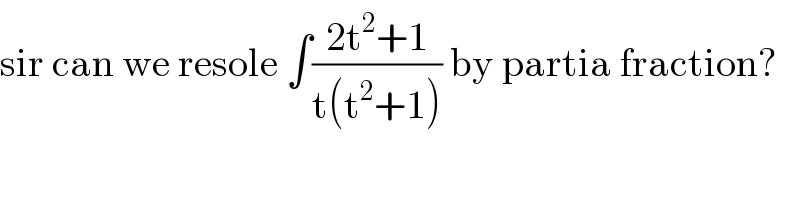
sir can we resole ∫((2t^2 +1)/(t(t^2 +1))) by partia fraction?
$$\mathrm{sir}\:\mathrm{can}\:\mathrm{we}\:\mathrm{resole}\:\int\frac{\mathrm{2t}^{\mathrm{2}} +\mathrm{1}}{\mathrm{t}\left(\mathrm{t}^{\mathrm{2}} +\mathrm{1}\right)}\:\mathrm{by}\:\mathrm{partia}\:\mathrm{fraction}? \\ $$
Commented by mathmax by abdo last updated on 10/May/20
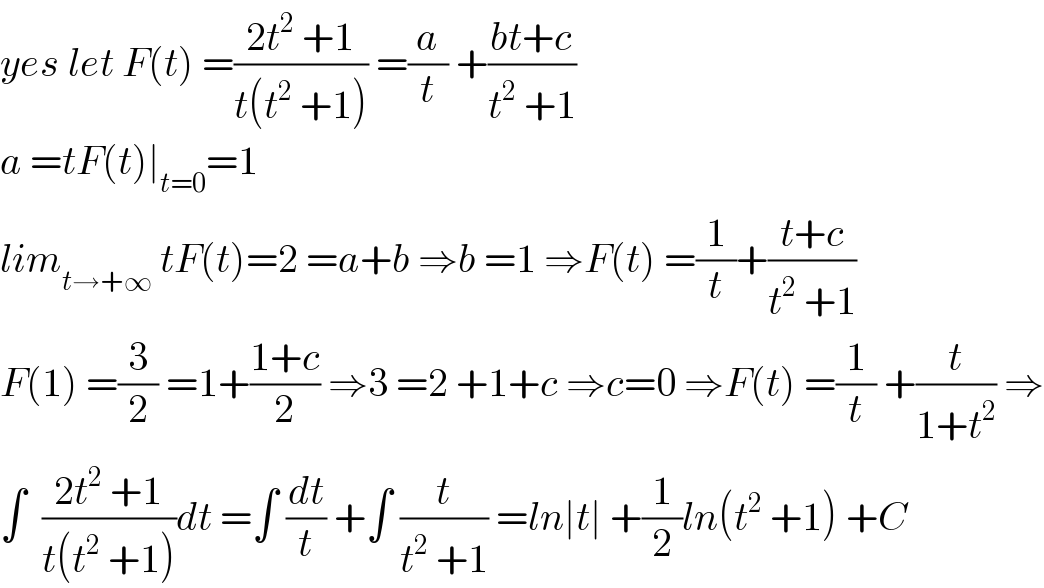
yes let F(t) =((2t^2 +1)/(t(t^2 +1))) =(a/t) +((bt+c)/(t^2 +1)) a =tF(t)∣_(t=0) =1 lim_(t→+∞) tF(t)=2 =a+b ⇒b =1 ⇒F(t) =(1/t)+((t+c)/(t^2 +1)) F(1) =(3/2) =1+((1+c)/2) ⇒3 =2 +1+c ⇒c=0 ⇒F(t) =(1/t) +(t/(1+t^2 )) ⇒ ∫ ((2t^2 +1)/(t(t^2 +1)))dt =∫ (dt/t) +∫ (t/(t^2 +1)) =ln∣t∣ +(1/2)ln(t^2 +1) +C
$${yes}\:{let}\:{F}\left({t}\right)\:=\frac{\mathrm{2}{t}^{\mathrm{2}} \:+\mathrm{1}}{{t}\left({t}^{\mathrm{2}} \:+\mathrm{1}\right)}\:=\frac{{a}}{{t}}\:+\frac{{bt}+{c}}{{t}^{\mathrm{2}} \:+\mathrm{1}} \\ $$$${a}\:={tF}\left({t}\right)\mid_{{t}=\mathrm{0}} =\mathrm{1} \\ $$$${lim}_{{t}\rightarrow+\infty} \:{tF}\left({t}\right)=\mathrm{2}\:={a}+{b}\:\Rightarrow{b}\:=\mathrm{1}\:\Rightarrow{F}\left({t}\right)\:=\frac{\mathrm{1}}{{t}}+\frac{{t}+{c}}{{t}^{\mathrm{2}} \:+\mathrm{1}} \\ $$$${F}\left(\mathrm{1}\right)\:=\frac{\mathrm{3}}{\mathrm{2}}\:=\mathrm{1}+\frac{\mathrm{1}+{c}}{\mathrm{2}}\:\Rightarrow\mathrm{3}\:=\mathrm{2}\:+\mathrm{1}+{c}\:\Rightarrow{c}=\mathrm{0}\:\Rightarrow{F}\left({t}\right)\:=\frac{\mathrm{1}}{{t}}\:+\frac{{t}}{\mathrm{1}+{t}^{\mathrm{2}} }\:\Rightarrow \\ $$$$\int\:\:\frac{\mathrm{2}{t}^{\mathrm{2}} \:+\mathrm{1}}{{t}\left({t}^{\mathrm{2}} \:+\mathrm{1}\right)}{dt}\:=\int\:\frac{{dt}}{{t}}\:+\int\:\frac{{t}}{{t}^{\mathrm{2}} \:+\mathrm{1}}\:={ln}\mid{t}\mid\:+\frac{\mathrm{1}}{\mathrm{2}}{ln}\left({t}^{\mathrm{2}} \:+\mathrm{1}\right)\:+{C} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *