Question Number 165794 by SANOGO last updated on 08/Feb/22
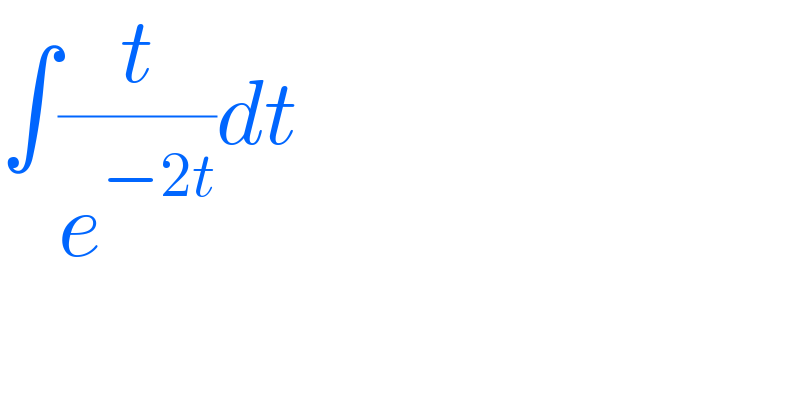
$$\int\frac{{t}}{{e}^{−\mathrm{2}{t}} }{dt} \\ $$
Answered by TheSupreme last updated on 08/Feb/22
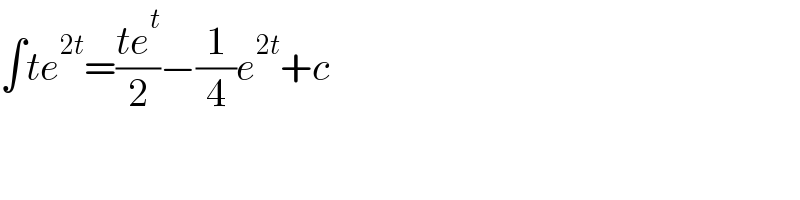
$$\int{te}^{\mathrm{2}{t}} =\frac{{te}^{{t}} }{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{4}}{e}^{\mathrm{2}{t}} +{c} \\ $$$$ \\ $$
Commented by alephzero last updated on 08/Feb/22

$$\mathrm{Reonsider}\:\frac{{te}^{\boldsymbol{{t}}} }{\mathrm{2}}.\:\mathrm{Are}\:\mathrm{you}\:\mathrm{sure}\:\mathrm{there} \\ $$$$\mathrm{is}\:\mathrm{only}\:\boldsymbol{{t}}? \\ $$
Answered by alephzero last updated on 08/Feb/22
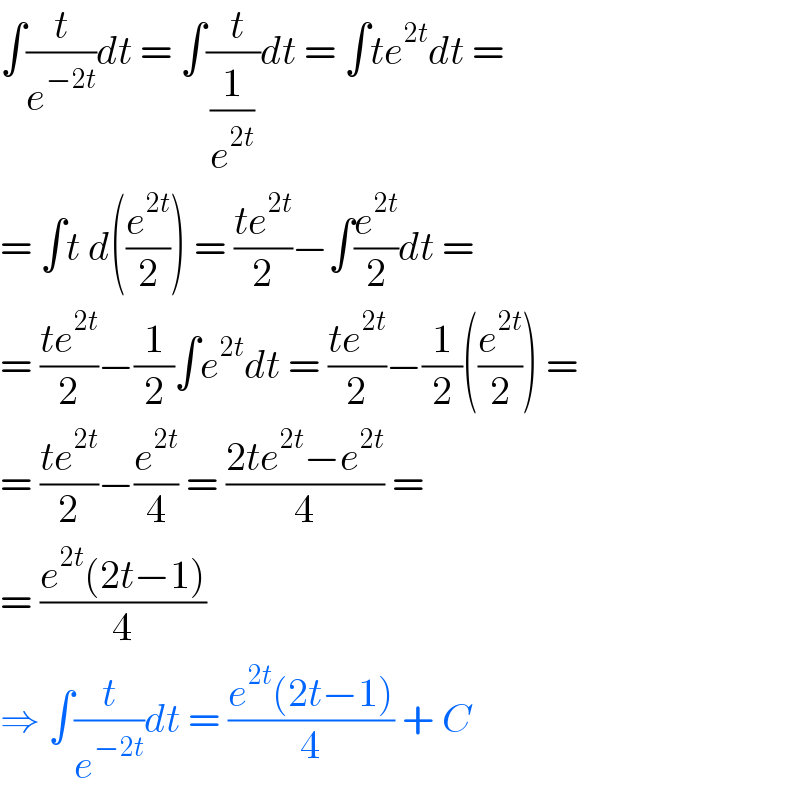
$$\int\frac{{t}}{{e}^{−\mathrm{2}{t}} }{dt}\:=\:\int\frac{\:\:\:{t}\:\:}{\frac{\mathrm{1}}{{e}^{\mathrm{2}{t}} }}{dt}\:=\:\int{te}^{\mathrm{2}{t}} {dt}\:= \\ $$$$=\:\int{t}\:{d}\left(\frac{{e}^{\mathrm{2}{t}} }{\mathrm{2}}\right)\:=\:\frac{{te}^{\mathrm{2}{t}} }{\mathrm{2}}−\int\frac{{e}^{\mathrm{2}{t}} }{\mathrm{2}}{dt}\:= \\ $$$$=\:\frac{{te}^{\mathrm{2}{t}} }{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}\int{e}^{\mathrm{2}{t}} {dt}\:=\:\frac{{te}^{\mathrm{2}{t}} }{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{{e}^{\mathrm{2}{t}} }{\mathrm{2}}\right)\:= \\ $$$$=\:\frac{{te}^{\mathrm{2}{t}} }{\mathrm{2}}−\frac{{e}^{\mathrm{2}{t}} }{\mathrm{4}}\:=\:\frac{\mathrm{2}{te}^{\mathrm{2}{t}} −{e}^{\mathrm{2}{t}} }{\mathrm{4}}\:= \\ $$$$=\:\frac{{e}^{\mathrm{2}{t}} \left(\mathrm{2}{t}−\mathrm{1}\right)}{\mathrm{4}}\: \\ $$$$\Rightarrow\:\int\frac{{t}}{{e}^{−\mathrm{2}{t}} }{dt}\:=\:\frac{{e}^{\mathrm{2}{t}} \left(\mathrm{2}{t}−\mathrm{1}\right)}{\mathrm{4}}\:+\:{C} \\ $$
