Menu Close

t-ml-t-g-l-sin-t-0-

Tinku Tara 0 Comments
Pin




Question Number 129985 by Dwaipayan Shikari last updated on 21/Jan/21
θ^(••) (t)−(γ/(ml))θ^• (t)+(g/l)sinθ(t)=0
θ∙∙(t)−γmlθ∙(t)+glsinθ(t)=0
Answered by Olaf last updated on 21/Jan/21
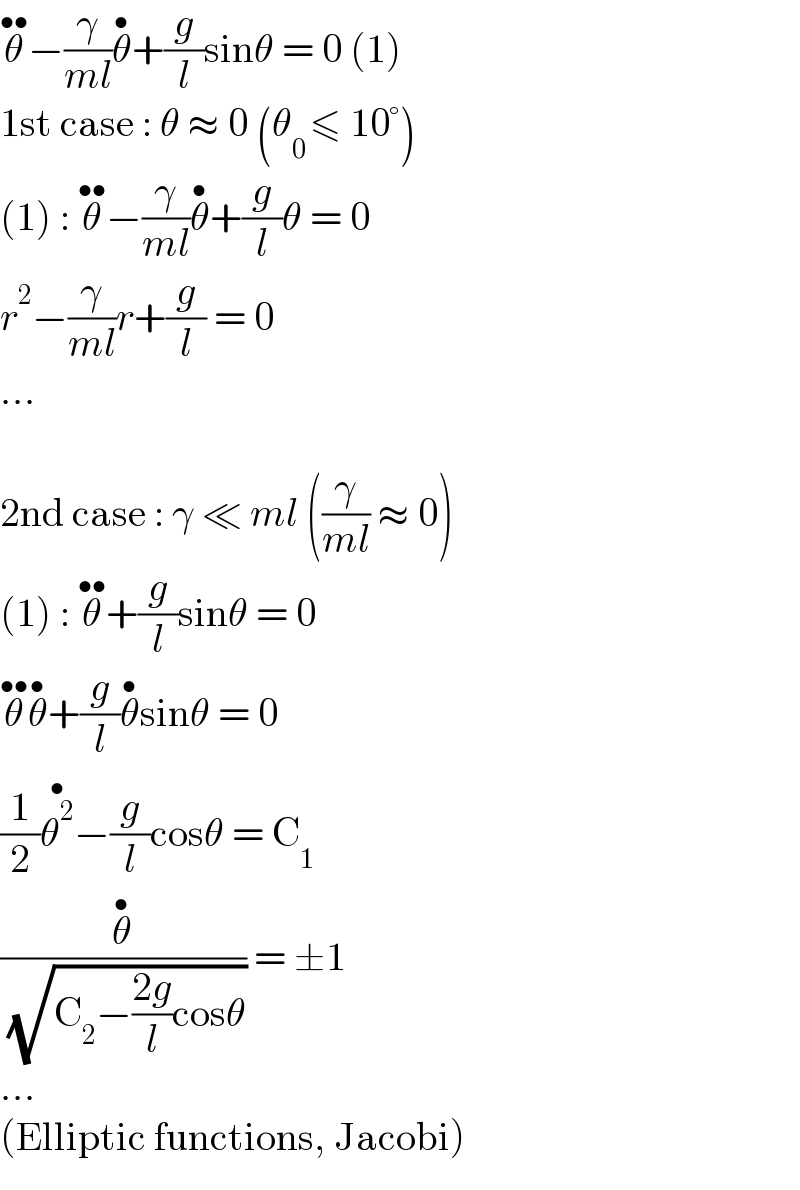
θ^(••) −(γ/(ml))θ^• +(g/l)sinθ = 0 (1) 1st case : θ ≈ 0 (θ_(0 ) ≤ 10°) (1) : θ^(••) −(γ/(ml))θ^• +(g/l)θ = 0 r^2 −(γ/(ml))r+(g/l) = 0 ... 2nd case : γ ≪ ml ((γ/(ml)) ≈ 0) (1) : θ^(••) +(g/l)sinθ = 0 θ^(••) θ^• +(g/l)θ^• sinθ = 0 (1/2)θ^2 ^(•) −(g/l)cosθ = C_1 (θ^• /( (√(C_2 −((2g)/l)cosθ)))) = ±1 ... (Elliptic functions, Jacobi)
θ∙∙−γmlθ∙+glsinθ=0(1)1stcase:θ≈0(θ0⩽10°)(1):θ∙∙−γmlθ∙+glθ=0r2−γmlr+gl=0…2ndcase:γ≪ml(γml≈0)(1):θ∙∙+glsinθ=0θ∙∙θ∙+glθ∙sinθ=012θ2∙−glcosθ=C1θ∙C2−2glcosθ=±1…(Ellipticfunctions,Jacobi)
Commented by Dwaipayan Shikari last updated on 21/Jan/21
Is it possible to solve it simaltaneously? Including (γ/(ml))θ^• and (g/l)sinθ ?
Isitpossibletosolveitsimaltaneously?Includingγmlθ∙andglsinθ?

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *