Question Number 120761 by bramlexs22 last updated on 02/Nov/20
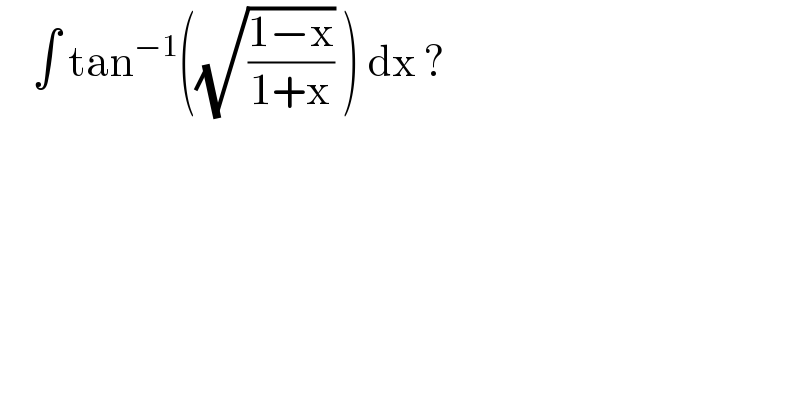
$$\:\:\:\:\int\:\mathrm{tan}^{−\mathrm{1}} \left(\sqrt{\frac{\mathrm{1}−\mathrm{x}}{\mathrm{1}+\mathrm{x}}}\:\right)\:\mathrm{dx}\:? \\ $$
Answered by liberty last updated on 02/Nov/20
![We put x = cos ψ ⇒dx = −sin ψ dψ ∫ tan^(−1) (√((1−cos ψ)/(1+cos ψ))) (−sin ψ dψ) = ∫ tan^(−1) (√((2sin^2 (ψ/2))/(2cos^2 (ψ/2)))) (−sin ψ dψ )= ∫ tan^(−1) (tan (ψ/2))(−sin ψ dψ) = ∫ −((ψ/2))sin ψ dψ = −(1/2)[ −ψ cos ψ+sin ψ ] +c =−(1/2)[ −x cos^(−1) (x)+(√(1−x^2 )) ] + c](https://www.tinkutara.com/question/Q120762.png)
$$\mathrm{We}\:\mathrm{put}\:\mathrm{x}\:=\:\mathrm{cos}\:\psi\:\Rightarrow\mathrm{dx}\:=\:−\mathrm{sin}\:\psi\:\mathrm{d}\psi \\ $$$$\int\:\mathrm{tan}^{−\mathrm{1}} \:\sqrt{\frac{\mathrm{1}−\mathrm{cos}\:\psi}{\mathrm{1}+\mathrm{cos}\:\psi}}\:\left(−\mathrm{sin}\:\psi\:\mathrm{d}\psi\right)\:= \\ $$$$\int\:\mathrm{tan}^{−\mathrm{1}} \sqrt{\frac{\mathrm{2sin}\:^{\mathrm{2}} \left(\psi/\mathrm{2}\right)}{\mathrm{2cos}\:^{\mathrm{2}} \left(\psi/\mathrm{2}\right)}}\:\left(−\mathrm{sin}\:\psi\:\mathrm{d}\psi\:\right)= \\ $$$$\int\:\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{tan}\:\left(\psi/\mathrm{2}\right)\right)\left(−\mathrm{sin}\:\psi\:\mathrm{d}\psi\right)\:= \\ $$$$\int\:−\left(\frac{\psi}{\mathrm{2}}\right)\mathrm{sin}\:\psi\:\mathrm{d}\psi\:=\:−\frac{\mathrm{1}}{\mathrm{2}}\left[\:−\psi\:\mathrm{cos}\:\psi+\mathrm{sin}\:\psi\:\right]\:+\mathrm{c} \\ $$$$\:=−\frac{\mathrm{1}}{\mathrm{2}}\left[\:−\mathrm{x}\:\mathrm{cos}^{−\mathrm{1}} \left(\mathrm{x}\right)+\sqrt{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }\:\right]\:+\:\mathrm{c}\: \\ $$
