tan-1-1-x-x-1-dx-

Question Number 112666 by bemath last updated on 09/Sep/20

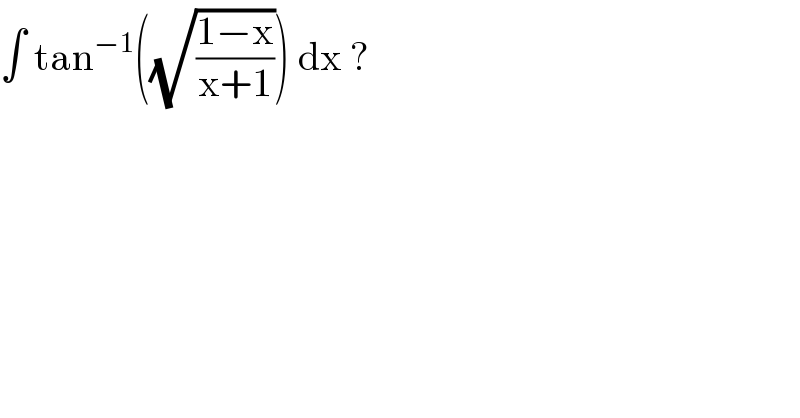
$$\int\:\mathrm{tan}^{−\mathrm{1}} \left(\sqrt{\frac{\mathrm{1}−\mathrm{x}}{\mathrm{x}+\mathrm{1}}}\right)\:\mathrm{dx}\:? \\ $$

Answered by Her_Majesty last updated on 09/Sep/20

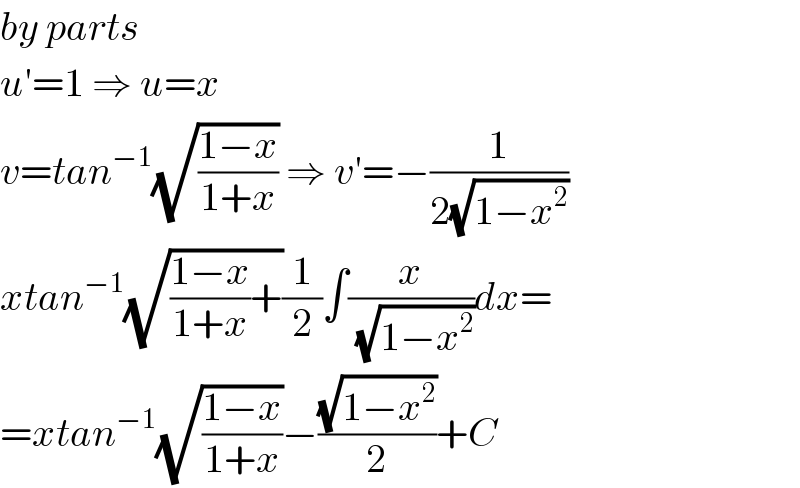
by parts u′=1 ⇒ u=x v=tan^(−1) (√((1−x)/(1+x))) ⇒ v′=−(1/(2(√(1−x^2 )))) xtan^(−1) (√(((1−x)/(1+x))+))(1/2)∫(x/( (√(1−x^2 ))))dx= =xtan^(−1) (√((1−x)/(1+x)))−((√(1−x^2 ))/2)+C

$${by}\:{parts} \\ $$$${u}'=\mathrm{1}\:\Rightarrow\:{u}={x} \\ $$$${v}={tan}^{−\mathrm{1}} \sqrt{\frac{\mathrm{1}−{x}}{\mathrm{1}+{x}}}\:\Rightarrow\:{v}'=−\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }} \\ $$$${xtan}^{−\mathrm{1}} \sqrt{\frac{\mathrm{1}−{x}}{\mathrm{1}+{x}}+}\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{x}}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}{dx}= \\ $$$$={xtan}^{−\mathrm{1}} \sqrt{\frac{\mathrm{1}−{x}}{\mathrm{1}+{x}}}−\frac{\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}{\mathrm{2}}+{C} \\ $$

Answered by bobhans last updated on 09/Sep/20

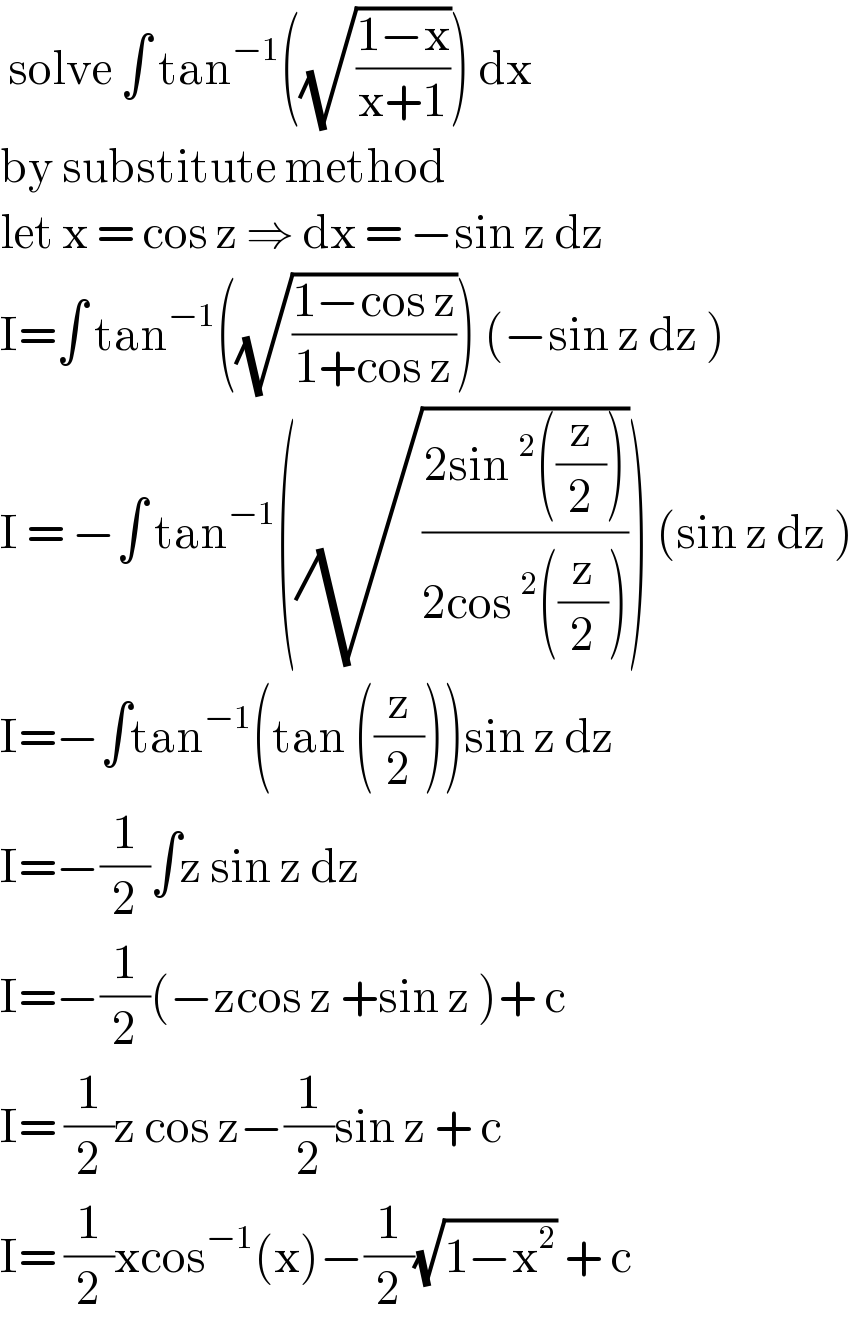
solve ∫ tan^(−1) ((√((1−x)/(x+1)))) dx by substitute method let x = cos z ⇒ dx = −sin z dz I=∫ tan^(−1) ((√((1−cos z)/(1+cos z)))) (−sin z dz ) I = −∫ tan^(−1) ((√((2sin^2 ((z/2)))/(2cos^2 ((z/2)))))) (sin z dz ) I=−∫tan^(−1) (tan ((z/2)))sin z dz I=−(1/2)∫z sin z dz I=−(1/2)(−zcos z +sin z )+ c I= (1/2)z cos z−(1/2)sin z + c I= (1/2)xcos^(−1) (x)−(1/2)(√(1−x^2 )) + c

$$\:\mathrm{solve}\:\int\:\mathrm{tan}^{−\mathrm{1}} \left(\sqrt{\frac{\mathrm{1}−\mathrm{x}}{\mathrm{x}+\mathrm{1}}}\right)\:\mathrm{dx}\: \\ $$$$\mathrm{by}\:\mathrm{substitute}\:\mathrm{method}\: \\ $$$$\mathrm{let}\:\mathrm{x}\:=\:\mathrm{cos}\:\mathrm{z}\:\Rightarrow\:\mathrm{dx}\:=\:−\mathrm{sin}\:\mathrm{z}\:\mathrm{dz} \\ $$$$\mathrm{I}=\int\:\mathrm{tan}^{−\mathrm{1}} \left(\sqrt{\frac{\mathrm{1}−\mathrm{cos}\:\mathrm{z}}{\mathrm{1}+\mathrm{cos}\:\mathrm{z}}}\right)\:\left(−\mathrm{sin}\:\mathrm{z}\:\mathrm{dz}\:\right) \\ $$$$\mathrm{I}\:=\:−\int\:\mathrm{tan}^{−\mathrm{1}} \left(\sqrt{\frac{\mathrm{2sin}\:^{\mathrm{2}} \left(\frac{\mathrm{z}}{\mathrm{2}}\right)}{\mathrm{2cos}\:^{\mathrm{2}} \left(\frac{\mathrm{z}}{\mathrm{2}}\right)}}\right)\:\left(\mathrm{sin}\:\mathrm{z}\:\mathrm{dz}\:\right) \\ $$$$\mathrm{I}=−\int\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{tan}\:\left(\frac{\mathrm{z}}{\mathrm{2}}\right)\right)\mathrm{sin}\:\mathrm{z}\:\mathrm{dz}\: \\ $$$$\mathrm{I}=−\frac{\mathrm{1}}{\mathrm{2}}\int\mathrm{z}\:\mathrm{sin}\:\mathrm{z}\:\mathrm{dz}\: \\ $$$$\mathrm{I}=−\frac{\mathrm{1}}{\mathrm{2}}\left(−\mathrm{zcos}\:\mathrm{z}\:+\mathrm{sin}\:\mathrm{z}\:\right)+\:\mathrm{c} \\ $$$$\mathrm{I}=\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{z}\:\mathrm{cos}\:\mathrm{z}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\:\mathrm{z}\:+\:\mathrm{c}\: \\ $$$$\mathrm{I}=\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{xcos}^{−\mathrm{1}} \left(\mathrm{x}\right)−\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }\:+\:\mathrm{c} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply