Question Number 92781 by i jagooll last updated on 09/May/20
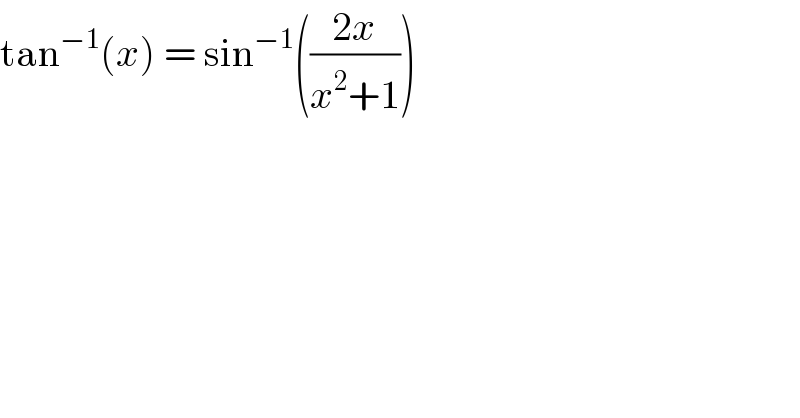
$$\mathrm{tan}^{−\mathrm{1}} \left({x}\right)\:=\:\mathrm{sin}^{−\mathrm{1}} \left(\frac{\mathrm{2}{x}}{{x}^{\mathrm{2}} +\mathrm{1}}\right)\: \\ $$
Commented by john santu last updated on 09/May/20
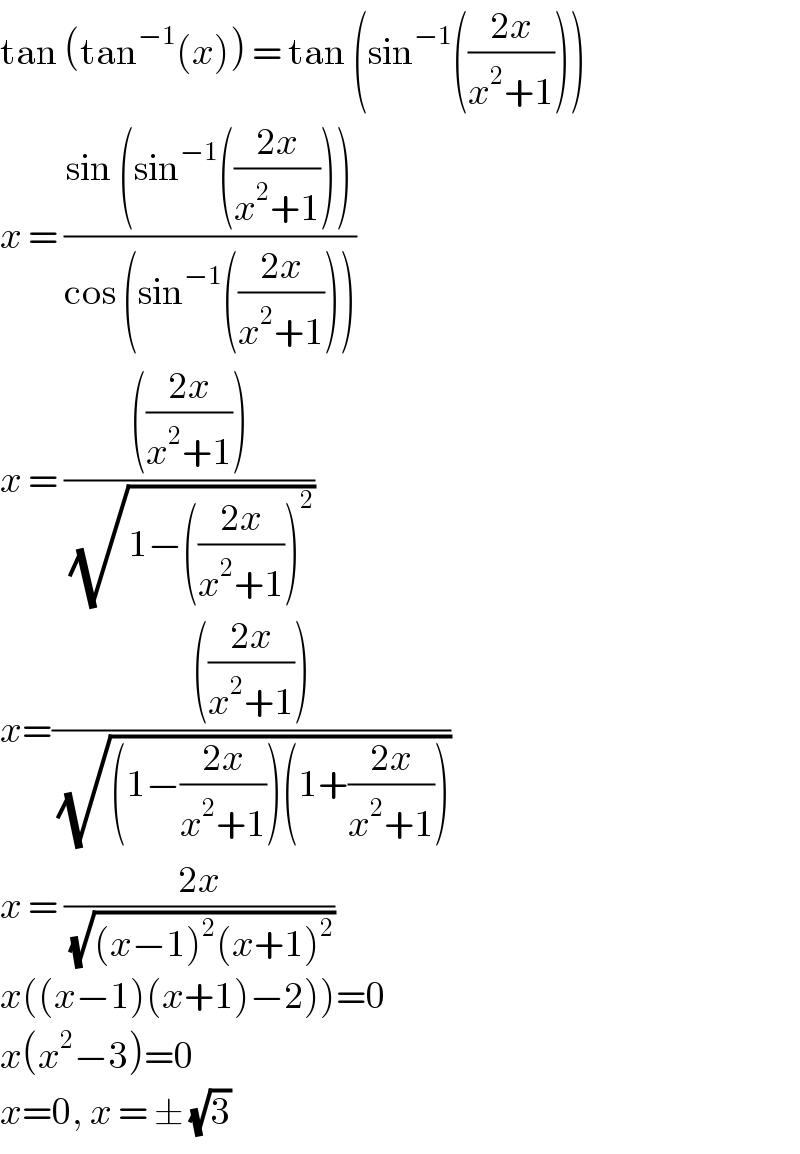
$$\mathrm{tan}\:\left(\mathrm{tan}^{−\mathrm{1}} \left({x}\right)\right)\:=\:\mathrm{tan}\:\left(\mathrm{sin}^{−\mathrm{1}} \left(\frac{\mathrm{2}{x}}{{x}^{\mathrm{2}} +\mathrm{1}}\right)\right) \\ $$$${x}\:=\:\frac{\mathrm{sin}\:\left(\mathrm{sin}^{−\mathrm{1}} \left(\frac{\mathrm{2}{x}}{{x}^{\mathrm{2}} +\mathrm{1}}\right)\right)}{\mathrm{cos}\:\left(\mathrm{sin}^{−\mathrm{1}} \left(\frac{\mathrm{2}{x}}{{x}^{\mathrm{2}} +\mathrm{1}}\right)\right)} \\ $$$${x}\:=\:\frac{\left(\frac{\mathrm{2}{x}}{{x}^{\mathrm{2}} +\mathrm{1}}\right)}{\:\sqrt{\mathrm{1}−\left(\frac{\mathrm{2}{x}}{{x}^{\mathrm{2}} +\mathrm{1}}\right)^{\mathrm{2}} }} \\ $$$${x}=\frac{\left(\frac{\mathrm{2}{x}}{{x}^{\mathrm{2}} +\mathrm{1}}\right)}{\:\sqrt{\left(\mathrm{1}−\frac{\mathrm{2}{x}}{{x}^{\mathrm{2}} +\mathrm{1}}\right)\left(\mathrm{1}+\frac{\mathrm{2}{x}}{{x}^{\mathrm{2}} +\mathrm{1}}\right)}} \\ $$$${x}\:=\:\frac{\mathrm{2}{x}}{\:\sqrt{\left({x}−\mathrm{1}\right)^{\mathrm{2}} \left({x}+\mathrm{1}\right)^{\mathrm{2}} }} \\ $$$$\left.{x}\left(\left({x}−\mathrm{1}\right)\left({x}+\mathrm{1}\right)−\mathrm{2}\right)\right)=\mathrm{0} \\ $$$${x}\left({x}^{\mathrm{2}} −\mathrm{3}\right)=\mathrm{0} \\ $$$${x}=\mathrm{0},\:{x}\:=\:\pm\:\sqrt{\mathrm{3}}\: \\ $$
Answered by Ar Brandon last updated on 09/May/20
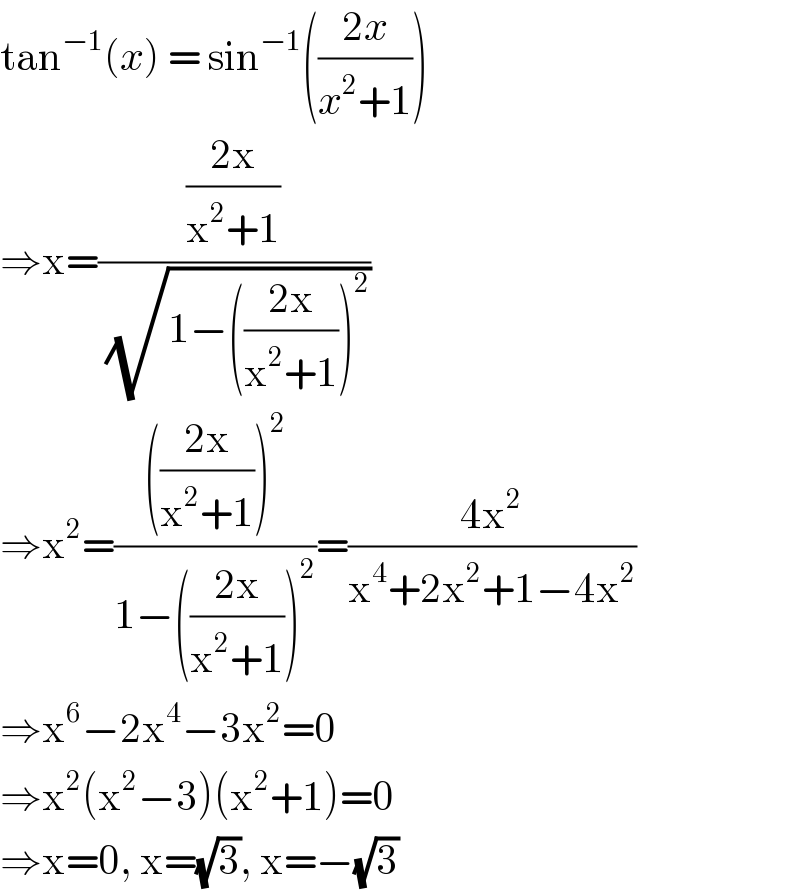
$$\mathrm{tan}^{−\mathrm{1}} \left({x}\right)\:=\:\mathrm{sin}^{−\mathrm{1}} \left(\frac{\mathrm{2}{x}}{{x}^{\mathrm{2}} +\mathrm{1}}\right) \\ $$$$\Rightarrow\mathrm{x}=\frac{\frac{\mathrm{2x}}{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}}{\:\sqrt{\mathrm{1}−\left(\frac{\mathrm{2x}}{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}\right)^{\mathrm{2}} }} \\ $$$$\Rightarrow\mathrm{x}^{\mathrm{2}} =\frac{\left(\frac{\mathrm{2x}}{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}\right)^{\mathrm{2}} }{\mathrm{1}−\left(\frac{\mathrm{2x}}{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}\right)^{\mathrm{2}} }=\frac{\mathrm{4x}^{\mathrm{2}} }{\mathrm{x}^{\mathrm{4}} +\mathrm{2x}^{\mathrm{2}} +\mathrm{1}−\mathrm{4x}^{\mathrm{2}} } \\ $$$$\Rightarrow\mathrm{x}^{\mathrm{6}} −\mathrm{2x}^{\mathrm{4}} −\mathrm{3x}^{\mathrm{2}} =\mathrm{0} \\ $$$$\Rightarrow\mathrm{x}^{\mathrm{2}} \left(\mathrm{x}^{\mathrm{2}} −\mathrm{3}\right)\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)=\mathrm{0} \\ $$$$\Rightarrow\mathrm{x}=\mathrm{0},\:\mathrm{x}=\sqrt{\mathrm{3}},\:\mathrm{x}=−\sqrt{\mathrm{3}} \\ $$
Commented by i jagooll last updated on 09/May/20
cool man ����
Commented by Ar Brandon last updated on 09/May/20
��
