Menu Close

tan-1-x-x-2-dx-

Tinku Tara 0 Comments
Pin




Question Number 51421 by Tawa1 last updated on 26/Dec/18
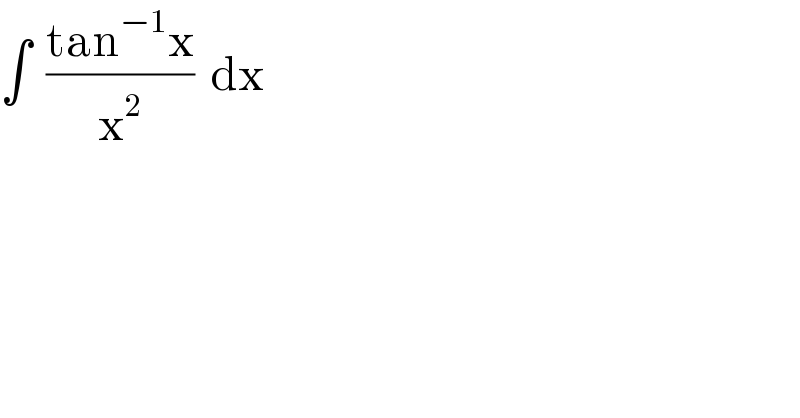
∫ ((tan^(−1) x)/x^2 ) dx
$$\int\:\:\frac{\mathrm{tan}^{−\mathrm{1}} \mathrm{x}}{\mathrm{x}^{\mathrm{2}} }\:\:\mathrm{dx} \\ $$
Commented by Tawa1 last updated on 27/Dec/18
God bless you sir
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Commented by maxmathsup by imad last updated on 26/Dec/18
let determine f(t) =∫ ((arctan(tx))/x^2 )dx with t>0 by parts f(t) =−(1/x) arctan(tx) −∫ −(1/x) (t/(1+t^2 x^2 ))dx =−((arctan(tx))/x) + t ∫ (dx/(x(1+t^2 x^2 ))) but ∫ (dx/(x(1+t^2 x^2 ))) =_(tx=u) ∫ (du/(t(u/t)(1+u^2 ))) = ∫ (du/(u(1+u^2 ))) =∫ ((1/u) −(u/(1+u^2 ))) =ln∣u∣ −(1/2)ln(1+u^2 ) = ln(((∣u∣)/( (√(1+u^2 ))))) +c =ln(((∣tx∣)/( (√(1+t^2 x^2 ))))) ⇒f(t) =−((arctan(tx))/x) +t ln(((∣tx∣)/( (√(1+t^2 x^2 )))))+c and ∫ ((arctan(x))/x^2 )dx =f(1) =−((arctanx)/x) +ln(((∣x∣)/( (√(1+x^2 )))))+C .
$${let}\:{determine}\:{f}\left({t}\right)\:=\int\:\:\frac{{arctan}\left({tx}\right)}{{x}^{\mathrm{2}} }{dx}\:\:{with}\:{t}>\mathrm{0}\:\:{by}\:{parts} \\ $$$${f}\left({t}\right)\:=−\frac{\mathrm{1}}{{x}}\:{arctan}\left({tx}\right)\:\:−\int\:\:−\frac{\mathrm{1}}{{x}}\:\:\frac{{t}}{\mathrm{1}+{t}^{\mathrm{2}} {x}^{\mathrm{2}} }{dx} \\ $$$$=−\frac{{arctan}\left({tx}\right)}{{x}}\:+\:{t}\:\int\:\:\:\:\:\frac{{dx}}{{x}\left(\mathrm{1}+{t}^{\mathrm{2}} {x}^{\mathrm{2}} \right)}\:{but} \\ $$$$\int\:\:\frac{{dx}}{{x}\left(\mathrm{1}+{t}^{\mathrm{2}} {x}^{\mathrm{2}} \right)}\:=_{{tx}={u}} \:\:\:\:\:\int\:\:\frac{{du}}{{t}\frac{{u}}{{t}}\left(\mathrm{1}+{u}^{\mathrm{2}} \right)}\:=\:\int\:\:\:\frac{{du}}{{u}\left(\mathrm{1}+{u}^{\mathrm{2}} \right)} \\ $$$$=\int\:\left(\frac{\mathrm{1}}{{u}}\:−\frac{{u}}{\mathrm{1}+{u}^{\mathrm{2}} }\right)\:={ln}\mid{u}\mid\:−\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\mathrm{1}+{u}^{\mathrm{2}} \right)\:=\:{ln}\left(\frac{\mid{u}\mid}{\:\sqrt{\mathrm{1}+{u}^{\mathrm{2}} }}\right)\:+{c} \\ $$$$={ln}\left(\frac{\mid{tx}\mid}{\:\sqrt{\mathrm{1}+{t}^{\mathrm{2}} \:{x}^{\mathrm{2}} }}\right)\:\Rightarrow{f}\left({t}\right)\:=−\frac{{arctan}\left({tx}\right)}{{x}}\:+{t}\:{ln}\left(\frac{\mid{tx}\mid}{\:\sqrt{\mathrm{1}+{t}^{\mathrm{2}} {x}^{\mathrm{2}} }}\right)+{c}\:\:{and} \\ $$$$\int\:\:\frac{{arctan}\left({x}\right)}{{x}^{\mathrm{2}} }{dx}\:={f}\left(\mathrm{1}\right)\:=−\frac{{arctanx}}{{x}}\:+{ln}\left(\frac{\mid{x}\mid}{\:\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}\right)+{C}\:. \\ $$
Commented by Abdo msup. last updated on 30/Dec/18
you are welcome sir.
$${you}\:{are}\:{welcome}\:{sir}. \\ $$
Answered by ajfour last updated on 26/Dec/18
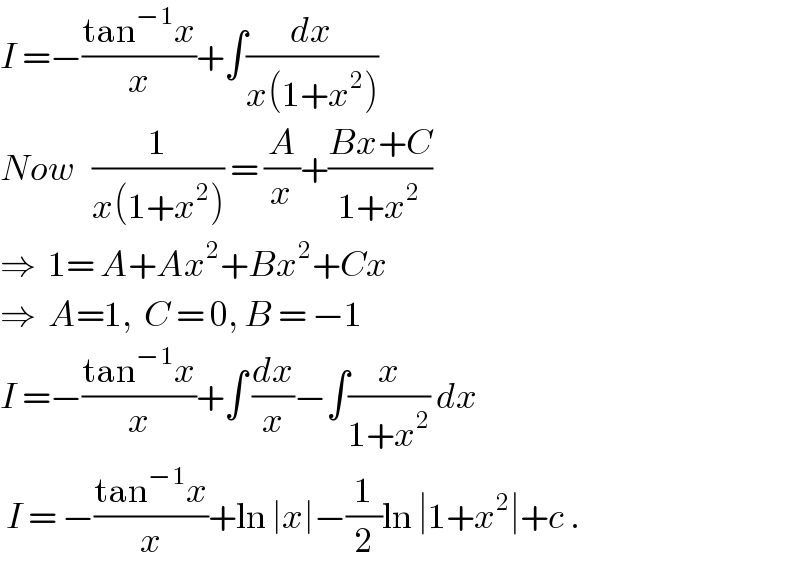
I =−((tan^(−1) x)/x)+∫(dx/(x(1+x^2 ))) Now (1/(x(1+x^2 ))) = (A/x)+((Bx+C)/(1+x^2 )) ⇒ 1= A+Ax^2 +Bx^2 +Cx ⇒ A=1, C = 0, B = −1 I =−((tan^(−1) x)/x)+∫ (dx/x)−∫(x/(1+x^2 )) dx I = −((tan^(−1) x)/x)+ln ∣x∣−(1/2)ln ∣1+x^2 ∣+c .
$${I}\:=−\frac{\mathrm{tan}^{−\mathrm{1}} {x}}{{x}}+\int\frac{{dx}}{{x}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)} \\ $$$${Now}\:\:\:\frac{\mathrm{1}}{{x}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)}\:=\:\frac{{A}}{{x}}+\frac{{Bx}+{C}}{\mathrm{1}+{x}^{\mathrm{2}} } \\ $$$$\Rightarrow\:\:\mathrm{1}=\:{A}+{Ax}^{\mathrm{2}} +{Bx}^{\mathrm{2}} +{Cx} \\ $$$$\Rightarrow\:\:{A}=\mathrm{1},\:\:{C}\:=\:\mathrm{0},\:{B}\:=\:−\mathrm{1} \\ $$$${I}\:=−\frac{\mathrm{tan}^{−\mathrm{1}} {x}}{{x}}+\int\:\frac{{dx}}{{x}}−\int\frac{{x}}{\mathrm{1}+{x}^{\mathrm{2}} }\:{dx} \\ $$$$\:{I}\:=\:−\frac{\mathrm{tan}^{−\mathrm{1}} {x}}{{x}}+\mathrm{ln}\:\mid{x}\mid−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\mid\mathrm{1}+{x}^{\mathrm{2}} \mid+{c}\:. \\ $$
Commented by Tawa1 last updated on 26/Dec/18
God bless you sir
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Answered by Smail last updated on 26/Dec/18
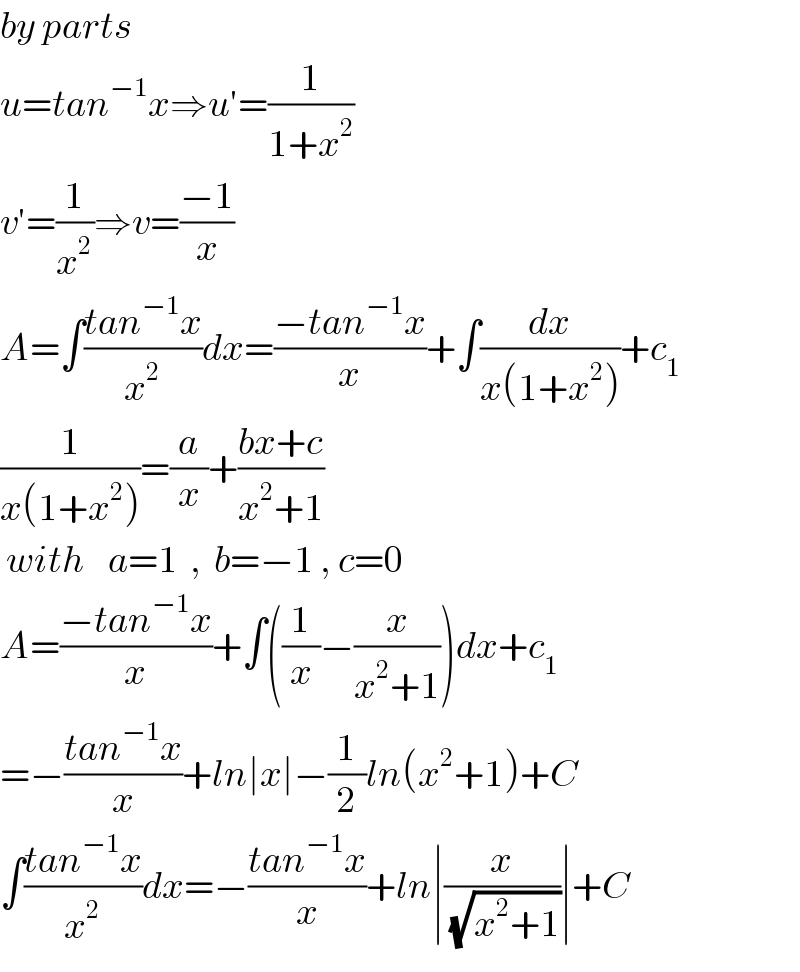
by parts u=tan^(−1) x⇒u′=(1/(1+x^2 )) v′=(1/x^2 )⇒v=((−1)/x) A=∫((tan^(−1) x)/x^2 )dx=((−tan^(−1) x)/x)+∫(dx/(x(1+x^2 )))+c_1 (1/(x(1+x^2 )))=(a/x)+((bx+c)/(x^2 +1)) with a=1 , b=−1 , c=0 A=((−tan^(−1) x)/x)+∫((1/x)−(x/(x^2 +1)))dx+c_1 =−((tan^(−1) x)/x)+ln∣x∣−(1/2)ln(x^2 +1)+C ∫((tan^(−1) x)/x^2 )dx=−((tan^(−1) x)/x)+ln∣(x/( (√(x^2 +1))))∣+C
$${by}\:{parts} \\ $$$${u}={tan}^{−\mathrm{1}} {x}\Rightarrow{u}'=\frac{\mathrm{1}}{\mathrm{1}+{x}^{\mathrm{2}} } \\ $$$${v}'=\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\Rightarrow{v}=\frac{−\mathrm{1}}{{x}} \\ $$$${A}=\int\frac{{tan}^{−\mathrm{1}} {x}}{{x}^{\mathrm{2}} }{dx}=\frac{−{tan}^{−\mathrm{1}} {x}}{{x}}+\int\frac{{dx}}{{x}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)}+{c}_{\mathrm{1}} \\ $$$$\frac{\mathrm{1}}{{x}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)}=\frac{{a}}{{x}}+\frac{{bx}+{c}}{{x}^{\mathrm{2}} +\mathrm{1}} \\ $$$$\:{with}\:\:\:\:{a}=\mathrm{1}\:\:,\:\:{b}=−\mathrm{1}\:,\:{c}=\mathrm{0} \\ $$$${A}=\frac{−{tan}^{−\mathrm{1}} {x}}{{x}}+\int\left(\frac{\mathrm{1}}{{x}}−\frac{{x}}{{x}^{\mathrm{2}} +\mathrm{1}}\right){dx}+{c}_{\mathrm{1}} \\ $$$$=−\frac{{tan}^{−\mathrm{1}} {x}}{{x}}+{ln}\mid{x}\mid−\frac{\mathrm{1}}{\mathrm{2}}{ln}\left({x}^{\mathrm{2}} +\mathrm{1}\right)+{C} \\ $$$$\int\frac{{tan}^{−\mathrm{1}} {x}}{{x}^{\mathrm{2}} }{dx}=−\frac{{tan}^{−\mathrm{1}} {x}}{{x}}+{ln}\mid\frac{{x}}{\:\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}}\mid+{C} \\ $$
Commented by Tawa1 last updated on 26/Dec/18
God bless you sir
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *