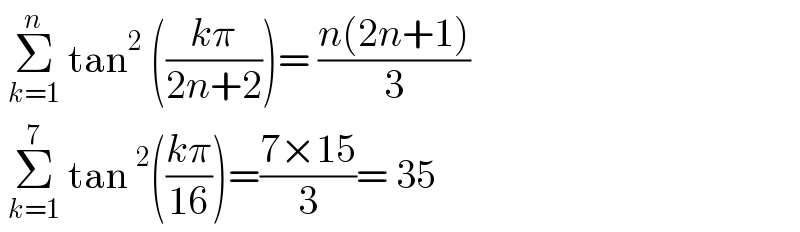tan-2-pi-16-tan-2-2pi-16-tan-2-7pi-16-

Question Number 155466 by cortano last updated on 01/Oct/21

\tan^{2} (\frac{π}{16}) + \tan^{2} (\frac{2 π}{16}) + \dots + \tan^{2} (\frac{7 π}{16}) = ?

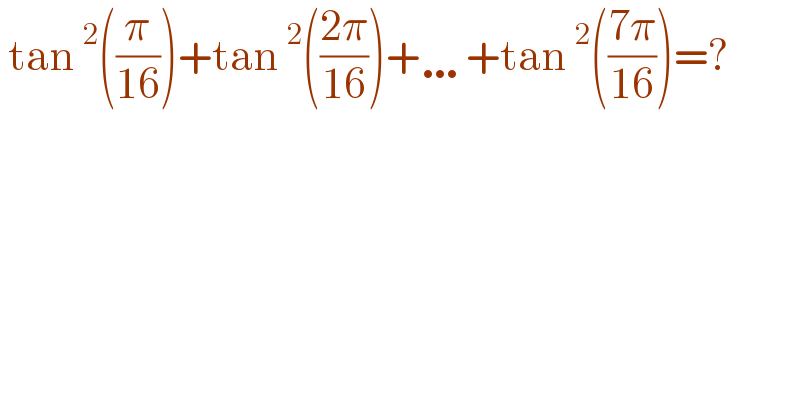
Commented by VIDDD last updated on 01/Oct/21

c a n u s h o w u s o l u t i o n

Commented by VIDDD last updated on 01/Oct/21

I wanna see ur sulotion plz

Answered by puissant last updated on 01/Oct/21

{t a n}^{2} (\frac{π}{16}) + {t a n}^{2} (\frac{2 π}{12}) + \dots + {t a n}^{2} (\frac{7 π}{16})

= \frac{4}{{s i n}^{2} (\frac{π}{8})} - 2 + \frac{4}{{s i n}^{2} (\frac{π}{4})} - 2 + \frac{4}{{s i n}^{2} (\frac{3 π}{8})} - 2 + {t a n}^{2} (\frac{π}{4})

= \frac{4}{{s i n}^{2} (\frac{π}{8})} + \frac{4}{{s i n}^{2} (\frac{3 π}{8})} + 3

= 4 (\frac{1}{{s i n}^{2} (\frac{π}{8})} + \frac{1}{{s i n}^{2} (\frac{3 π}{8})}) + 3

= 4 (\frac{{s i n}^{2} (\frac{π}{8}) + {c o s}^{2} (\frac{π}{8})}{{s i n}^{2} (\frac{π}{8}) {c o s}^{2} (\frac{π}{8})}) + 3

= \frac{16}{{s i n}^{2} (\frac{π}{4})} + 3 = 32 + 3 = 35 . .

∴∵ S = \underset{k = 1}{\sum^{7}} {t a n}^{2} (\frac{k π}{16}) = 35 \dots

\dots \dots \dots \dots \dots L e p u i s s a n t \dots \dots \dots \dots \dots .

Commented by VIDDD last updated on 01/Oct/21

thanks sir ♡

Commented by peter frank last updated on 01/Oct/21

great

Answered by john_santu last updated on 01/Oct/21

\underset{k = 1}{\sum^{n}} \tan^{2} (\frac{k π}{2 n + 2}) = \frac{n (2 n + 1)}{3}

\underset{k = 1}{\sum^{7}} \tan^{2} (\frac{k π}{16}) = \frac{7 \times 15}{3} = 35