Question Number 20366 by ajfour last updated on 26/Aug/17
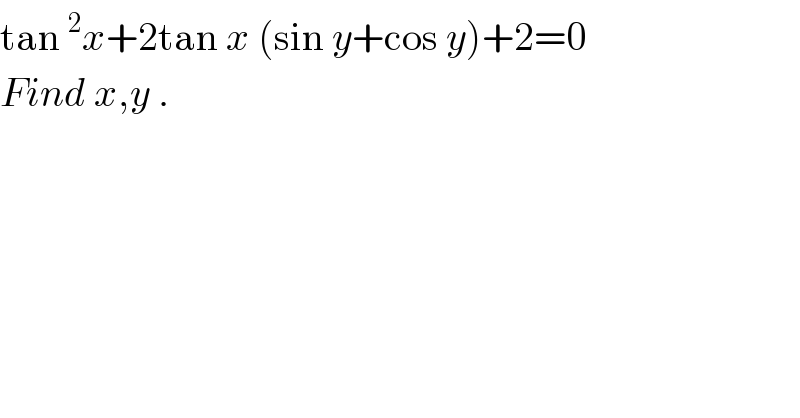
$$\mathrm{tan}\:^{\mathrm{2}} {x}+\mathrm{2tan}\:{x}\:\left(\mathrm{sin}\:{y}+\mathrm{cos}\:{y}\right)+\mathrm{2}=\mathrm{0} \\ $$$${Find}\:{x},{y}\:. \\ $$
Answered by mrW1 last updated on 26/Aug/17
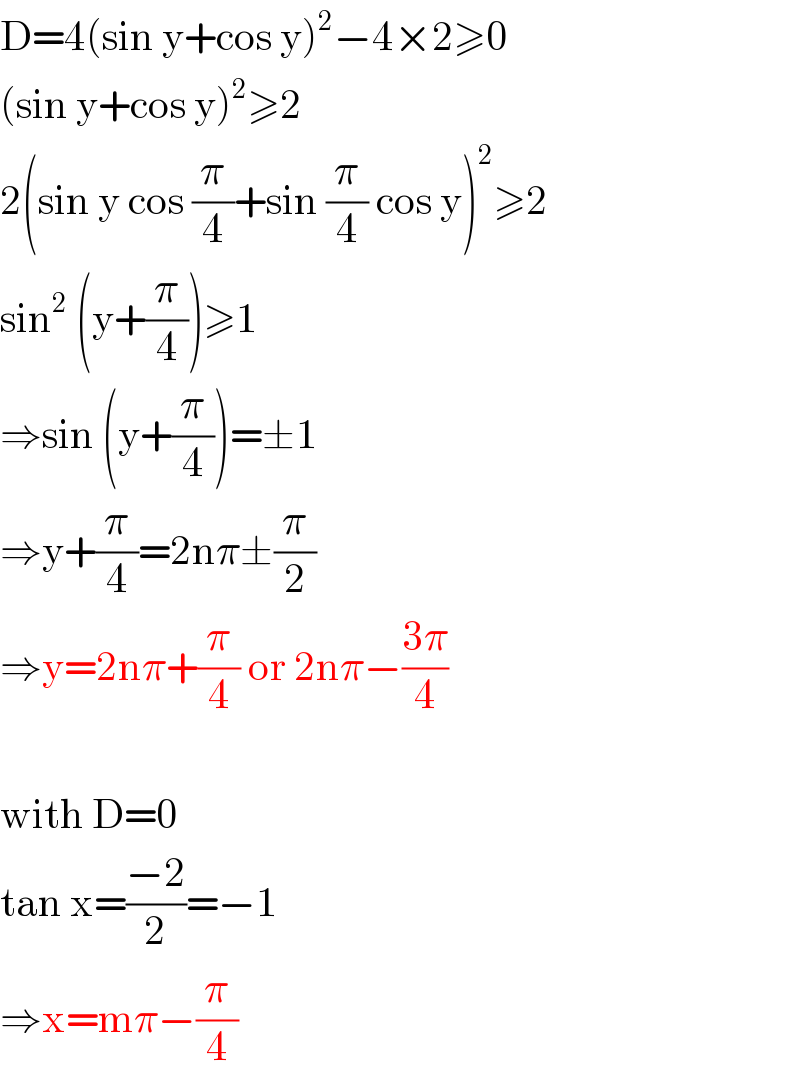
$$\mathrm{D}=\mathrm{4}\left(\mathrm{sin}\:\mathrm{y}+\mathrm{cos}\:\mathrm{y}\right)^{\mathrm{2}} −\mathrm{4}×\mathrm{2}\geqslant\mathrm{0} \\ $$$$\left(\mathrm{sin}\:\mathrm{y}+\mathrm{cos}\:\mathrm{y}\right)^{\mathrm{2}} \geqslant\mathrm{2} \\ $$$$\mathrm{2}\left(\mathrm{sin}\:\mathrm{y}\:\mathrm{cos}\:\frac{\pi}{\mathrm{4}}+\mathrm{sin}\:\frac{\pi}{\mathrm{4}}\:\mathrm{cos}\:\mathrm{y}\right)^{\mathrm{2}} \geqslant\mathrm{2} \\ $$$$\mathrm{sin}^{\mathrm{2}} \:\left(\mathrm{y}+\frac{\pi}{\mathrm{4}}\right)\geqslant\mathrm{1} \\ $$$$\Rightarrow\mathrm{sin}\:\left(\mathrm{y}+\frac{\pi}{\mathrm{4}}\right)=\pm\mathrm{1} \\ $$$$\Rightarrow\mathrm{y}+\frac{\pi}{\mathrm{4}}=\mathrm{2n}\pi\pm\frac{\pi}{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{y}=\mathrm{2n}\pi+\frac{\pi}{\mathrm{4}}\:\mathrm{or}\:\mathrm{2n}\pi−\frac{\mathrm{3}\pi}{\mathrm{4}} \\ $$$$ \\ $$$$\mathrm{with}\:\mathrm{D}=\mathrm{0} \\ $$$$\mathrm{tan}\:\mathrm{x}=\frac{−\mathrm{2}}{\mathrm{2}}=−\mathrm{1} \\ $$$$\Rightarrow\mathrm{x}=\mathrm{m}\pi−\frac{\pi}{\mathrm{4}} \\ $$
Commented by ajfour last updated on 26/Aug/17

$${thanks}\:{a}\:{lot},\:{sir}\:! \\ $$
