Question Number 116024 by mohammad17 last updated on 30/Sep/20
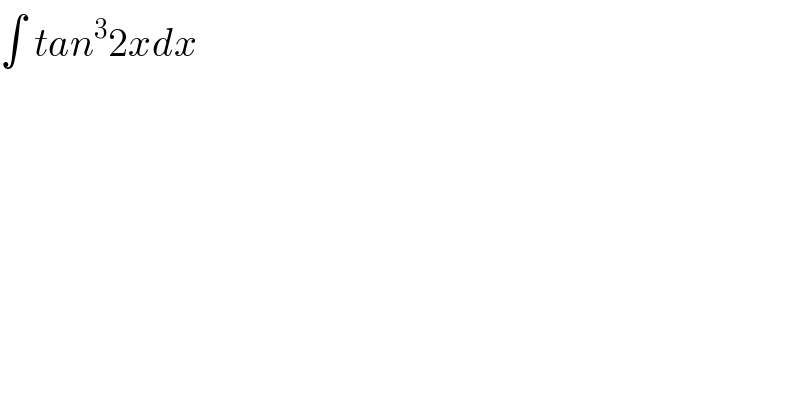
$$\int\:{tan}^{\mathrm{3}} \mathrm{2}{xdx} \\ $$
Answered by bemath last updated on 30/Sep/20
![= (1/2)∫ tan (2x)(sec^2 2x−1) d(2x) = (1/2)[ ∫ tan (2x) d(tan (2x)] −∫ ((sin (2x))/(cos (2x))) d(2x) = (1/(2 )) [(1/2)tan^2 (2x) +ln (cos (2x))]+c =(1/4)tan^2 (2x)+(1/2)ln (cos (2x)) + c](https://www.tinkutara.com/question/Q116026.png)
$$=\:\frac{\mathrm{1}}{\mathrm{2}}\int\:\mathrm{tan}\:\left(\mathrm{2}{x}\right)\left(\mathrm{sec}\:^{\mathrm{2}} \mathrm{2}{x}−\mathrm{1}\right)\:{d}\left(\mathrm{2}{x}\right) \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{2}}\left[\:\int\:\mathrm{tan}\:\left(\mathrm{2}{x}\right)\:{d}\left(\mathrm{tan}\:\left(\mathrm{2}{x}\right)\right]\:−\int\:\frac{\mathrm{sin}\:\left(\mathrm{2}{x}\right)}{\mathrm{cos}\:\left(\mathrm{2}{x}\right)}\:{d}\left(\mathrm{2}{x}\right)\right. \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{2}\:}\:\left[\frac{\mathrm{1}}{\mathrm{2}}\mathrm{tan}\:^{\mathrm{2}} \left(\mathrm{2}{x}\right)\:+\mathrm{ln}\:\left(\mathrm{cos}\:\left(\mathrm{2}{x}\right)\right)\right]+{c}\: \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\mathrm{tan}\:^{\mathrm{2}} \left(\mathrm{2}{x}\right)+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\left(\mathrm{cos}\:\left(\mathrm{2}{x}\right)\right)\:+\:{c} \\ $$
Answered by Dwaipayan Shikari last updated on 30/Sep/20
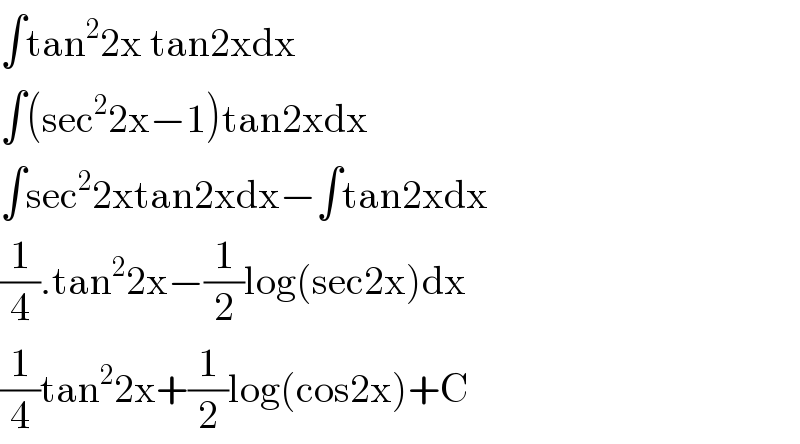
$$\int\mathrm{tan}^{\mathrm{2}} \mathrm{2x}\:\mathrm{tan2xdx} \\ $$$$\int\left(\mathrm{sec}^{\mathrm{2}} \mathrm{2x}−\mathrm{1}\right)\mathrm{tan2xdx} \\ $$$$\int\mathrm{sec}^{\mathrm{2}} \mathrm{2xtan2xdx}−\int\mathrm{tan2xdx} \\ $$$$\frac{\mathrm{1}}{\mathrm{4}}.\mathrm{tan}^{\mathrm{2}} \mathrm{2x}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{log}\left(\mathrm{sec2x}\right)\mathrm{dx} \\ $$$$\frac{\mathrm{1}}{\mathrm{4}}\mathrm{tan}^{\mathrm{2}} \mathrm{2x}+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{log}\left(\mathrm{cos2x}\right)+\mathrm{C} \\ $$
Answered by MJS_new last updated on 30/Sep/20
![∫tan^3 2x dx= [t=tan^3 2x → dx=(dt/(6t^(3/2) (t^(3/2) +1)))] =(1/6)∫(t^(1/3) /(t^(2/3) +1))dt=(1/6)∫(dt/t^(1/3) )−(1/6)∫(dt/(t^(1/3) (t^(2/3) +1)))= [u=t^(2/3) → dt=(3/2)t^(1/3) dt in the 2^(nd) one] =(1/4)t^(2/3) −(1/4)ln (t^(2/3) +1) = =(1/4)tan^2 2x −(1/4)ln (1+tan^2 2x) +C](https://www.tinkutara.com/question/Q116032.png)
$$\int\mathrm{tan}^{\mathrm{3}} \:\mathrm{2}{x}\:{dx}= \\ $$$$\:\:\:\:\:\left[{t}=\mathrm{tan}^{\mathrm{3}} \:\mathrm{2}{x}\:\rightarrow\:{dx}=\frac{{dt}}{\mathrm{6}{t}^{\mathrm{3}/\mathrm{2}} \left({t}^{\mathrm{3}/\mathrm{2}} +\mathrm{1}\right)}\right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{6}}\int\frac{{t}^{\mathrm{1}/\mathrm{3}} }{{t}^{\mathrm{2}/\mathrm{3}} +\mathrm{1}}{dt}=\frac{\mathrm{1}}{\mathrm{6}}\int\frac{{dt}}{{t}^{\mathrm{1}/\mathrm{3}} }−\frac{\mathrm{1}}{\mathrm{6}}\int\frac{{dt}}{{t}^{\mathrm{1}/\mathrm{3}} \left({t}^{\mathrm{2}/\mathrm{3}} +\mathrm{1}\right)}= \\ $$$$\:\:\:\:\:\left[{u}={t}^{\mathrm{2}/\mathrm{3}} \:\rightarrow\:{dt}=\frac{\mathrm{3}}{\mathrm{2}}{t}^{\mathrm{1}/\mathrm{3}} {dt}\:\mathrm{in}\:\mathrm{the}\:\mathrm{2}^{\mathrm{nd}} \:\mathrm{one}\right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}{t}^{\mathrm{2}/\mathrm{3}} −\frac{\mathrm{1}}{\mathrm{4}}\mathrm{ln}\:\left({t}^{\mathrm{2}/\mathrm{3}} +\mathrm{1}\right)\:= \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\mathrm{tan}^{\mathrm{2}} \:\mathrm{2}{x}\:−\frac{\mathrm{1}}{\mathrm{4}}\mathrm{ln}\:\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \:\mathrm{2}{x}\right)\:+{C} \\ $$
Answered by mnjuly1970 last updated on 30/Sep/20
![2x=t⇒dx=(1/2)dt I=(1/2)∫tan^3 (t)dt=(1/2)∫[tan^3 (t)+tan(t)−tann(t)]dt =(1/2)∫tan(t)(1+tan^2 (t))dt+(1/2)ln(cos(t))+C =(1/4)tan^2 (t)+(1/2)ln(cos(t))+C =(1/4)tan^2 (2x)+(1/2)ln(cos(2x))+C](https://www.tinkutara.com/question/Q116047.png)
$$\mathrm{2}{x}={t}\Rightarrow{dx}=\frac{\mathrm{1}}{\mathrm{2}}{dt} \\ $$$$ \\ $$$${I}=\frac{\mathrm{1}}{\mathrm{2}}\int{tan}^{\mathrm{3}} \left({t}\right){dt}=\frac{\mathrm{1}}{\mathrm{2}}\int\left[{tan}^{\mathrm{3}} \left({t}\right)+{tan}\left({t}\right)−{tann}\left({t}\right)\right]{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int{tan}\left({t}\right)\left(\mathrm{1}+{tan}^{\mathrm{2}} \left({t}\right)\right){dt}+\frac{\mathrm{1}}{\mathrm{2}}{ln}\left({cos}\left({t}\right)\right)+{C} \\ $$$$\:\:\:=\frac{\mathrm{1}}{\mathrm{4}}{tan}^{\mathrm{2}} \left({t}\right)+\frac{\mathrm{1}}{\mathrm{2}}{ln}\left({cos}\left({t}\right)\right)+{C} \\ $$$$ \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}{tan}^{\mathrm{2}} \left(\mathrm{2}{x}\right)+\frac{\mathrm{1}}{\mathrm{2}}{ln}\left({cos}\left(\mathrm{2}{x}\right)\right)+{C} \\ $$
