tan-m-m-1-tan-1-2m-1-

Question Number 167502 by cortano1 last updated on 18/Mar/22

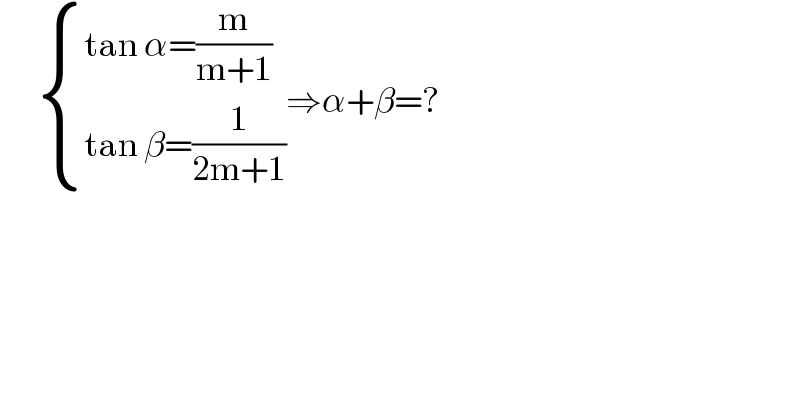
{ ((tan α=(m/(m+1)))),((tan β=(1/(2m+1)))) :}⇒α+β=?

$$\:\:\:\:\:\:\begin{cases}{\mathrm{tan}\:\alpha=\frac{\mathrm{m}}{\mathrm{m}+\mathrm{1}}}\\{\mathrm{tan}\:\beta=\frac{\mathrm{1}}{\mathrm{2m}+\mathrm{1}}}\end{cases}\Rightarrow\alpha+\beta=? \\ $$

Answered by Rasheed.Sindhi last updated on 18/Mar/22

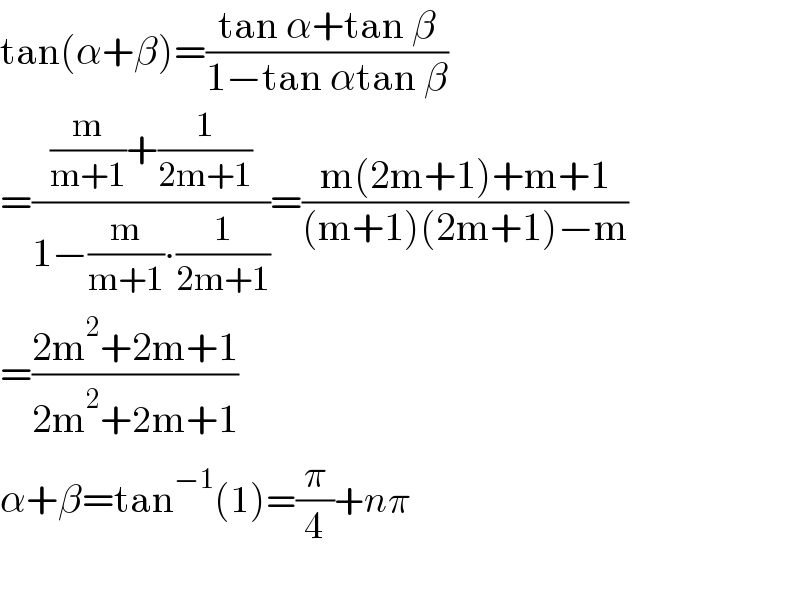
tan(α+β)=((tan α+tan β)/(1−tan αtan β)) =(((m/(m+1))+(1/(2m+1)))/(1−(m/(m+1))∙(1/(2m+1))))=((m(2m+1)+m+1)/((m+1)(2m+1)−m)) =((2m^2 +2m+1)/(2m^2 +2m+1)) α+β=tan^(−1) (1)=(π/4)+nπ

$$\mathrm{tan}\left(\alpha+\beta\right)=\frac{\mathrm{tan}\:\alpha+\mathrm{tan}\:\beta}{\mathrm{1}−\mathrm{tan}\:\alpha\mathrm{tan}\:\beta}\: \\ $$$$=\frac{\frac{\mathrm{m}}{\mathrm{m}+\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{2m}+\mathrm{1}}}{\mathrm{1}−\frac{\mathrm{m}}{\mathrm{m}+\mathrm{1}}\centerdot\frac{\mathrm{1}}{\mathrm{2m}+\mathrm{1}}}=\frac{\mathrm{m}\left(\mathrm{2m}+\mathrm{1}\right)+\mathrm{m}+\mathrm{1}}{\left(\mathrm{m}+\mathrm{1}\right)\left(\mathrm{2m}+\mathrm{1}\right)−\mathrm{m}} \\ $$$$=\frac{\mathrm{2m}^{\mathrm{2}} +\mathrm{2m}+\mathrm{1}}{\mathrm{2m}^{\mathrm{2}} +\mathrm{2m}+\mathrm{1}} \\ $$$$\alpha+\beta=\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{1}\right)=\frac{\pi}{\mathrm{4}}+{n}\pi\: \\ $$$$ \\ $$

Facebook Tweet Pin

tan-m-m-1-tan-1-2m-1-

Leave a Reply Cancel reply