Question Number 96260 by bemath last updated on 31/May/20
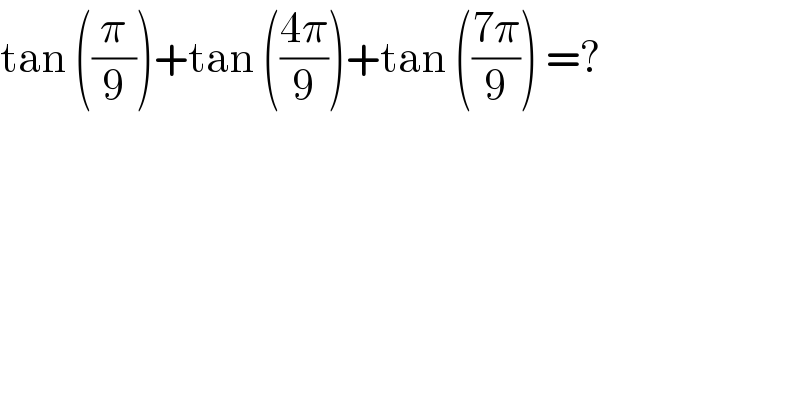
$$\mathrm{tan}\:\left(\frac{\pi}{\mathrm{9}}\right)+\mathrm{tan}\:\left(\frac{\mathrm{4}\pi}{\mathrm{9}}\right)+\mathrm{tan}\:\left(\frac{\mathrm{7}\pi}{\mathrm{9}}\right)\:=? \\ $$
Answered by john santu last updated on 31/May/20

$$\mathrm{set}\:{x}\:=\:\frac{\pi}{\mathrm{9}},\:\frac{\mathrm{4}\pi}{\mathrm{9}},\:\frac{\mathrm{7}\pi}{\mathrm{9}} \\ $$$$\mathrm{3}{x}\:=\:\frac{\pi}{\mathrm{3}},\:\frac{\mathrm{4}\pi}{\mathrm{3}},\:\frac{\mathrm{7}\pi}{\mathrm{3}}\: \\ $$$$\mathrm{tan}\:\mathrm{3}{x}\:=\:\mathrm{tan}\:\frac{\pi}{\mathrm{3}}=\mathrm{tan}\:\frac{\mathrm{4}\pi}{\mathrm{3}}=\mathrm{tan}\:\frac{\mathrm{7}\pi}{\mathrm{3}}\:=\:\sqrt{\mathrm{3}} \\ $$$$\mathrm{let}\:{q}\:=\:\mathrm{tan}\:{x}\:\Rightarrow\mathrm{tan}\:\mathrm{3}{x}\:=\:\frac{\mathrm{3}{q}−{q}^{\mathrm{3}} }{\mathrm{1}−\mathrm{3}{q}^{\mathrm{2}} } \\ $$$$\Rightarrow\sqrt{\mathrm{3}}\:−\mathrm{3}\sqrt{\mathrm{3}}\:{q}^{\mathrm{2}} \:=\:\mathrm{3}{q}−{q}^{\mathrm{3}} \\ $$$${q}^{\mathrm{3}} −\mathrm{3}\sqrt{\mathrm{3}}\:{q}^{\mathrm{2}} \:−\mathrm{3}{q}+\sqrt{\mathrm{3}}\:=\:\mathrm{0} \\ $$$${have}\:{roots}\:{are}\:\mathrm{tan}\:\frac{\pi}{\mathrm{9}},\:\mathrm{tan}\:\frac{\mathrm{4}\pi}{\mathrm{9}},\:\mathrm{tan}\:\frac{\mathrm{7}\pi}{\mathrm{9}} \\ $$$$\mathrm{by}\:\mathrm{Vieta}'\mathrm{s}\:\mathrm{rule}\: \\ $$$$\mathrm{tan}\:\frac{\pi}{\mathrm{9}}\:+\:\mathrm{tan}\:\frac{\mathrm{4}\pi}{\mathrm{9}}\:+\:\mathrm{tan}\:\frac{\mathrm{7}\pi}{\mathrm{9}}\:=\:\mathrm{3}\sqrt{\mathrm{3}}\: \\ $$
