Question Number 25335 by mubeen897@hotmail.com last updated on 08/Dec/17
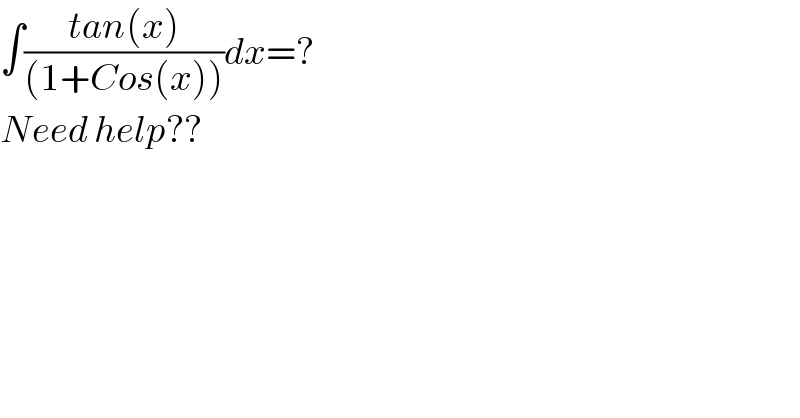
$$\int\frac{{tan}\left({x}\right)}{\left(\mathrm{1}+{Cos}\left({x}\right)\right)}{dx}=? \\ $$$${Need}\:{help}?? \\ $$$$ \\ $$
Answered by ajfour last updated on 08/Dec/17
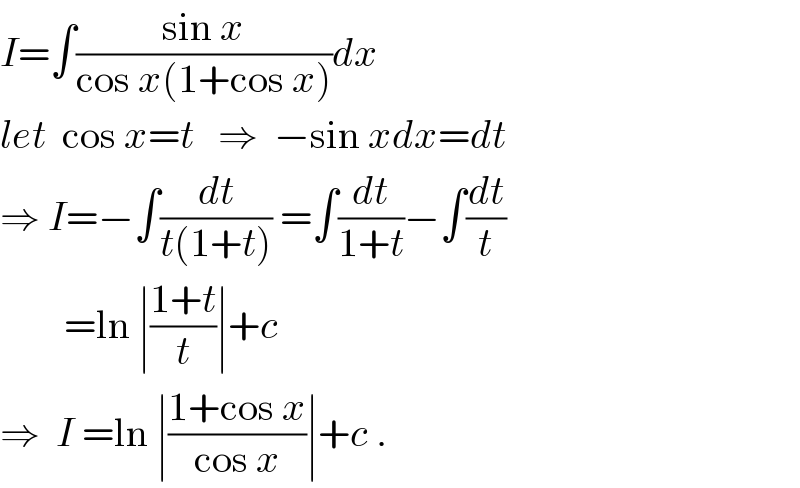
$${I}=\int\frac{\mathrm{sin}\:{x}}{\mathrm{cos}\:{x}\left(\mathrm{1}+\mathrm{cos}\:{x}\right)}{dx} \\ $$$${let}\:\:\mathrm{cos}\:{x}={t}\:\:\:\Rightarrow\:\:−\mathrm{sin}\:{xdx}={dt} \\ $$$$\Rightarrow\:{I}=−\int\frac{{dt}}{{t}\left(\mathrm{1}+{t}\right)}\:=\int\frac{{dt}}{\mathrm{1}+{t}}−\int\frac{{dt}}{{t}} \\ $$$$\:\:\:\:\:\:\:\:=\mathrm{ln}\:\mid\frac{\mathrm{1}+{t}}{{t}}\mid+{c} \\ $$$$\Rightarrow\:\:{I}\:=\mathrm{ln}\:\mid\frac{\mathrm{1}+\mathrm{cos}\:{x}}{\mathrm{cos}\:{x}}\mid+{c}\:. \\ $$
Answered by $@ty@m last updated on 08/Dec/17
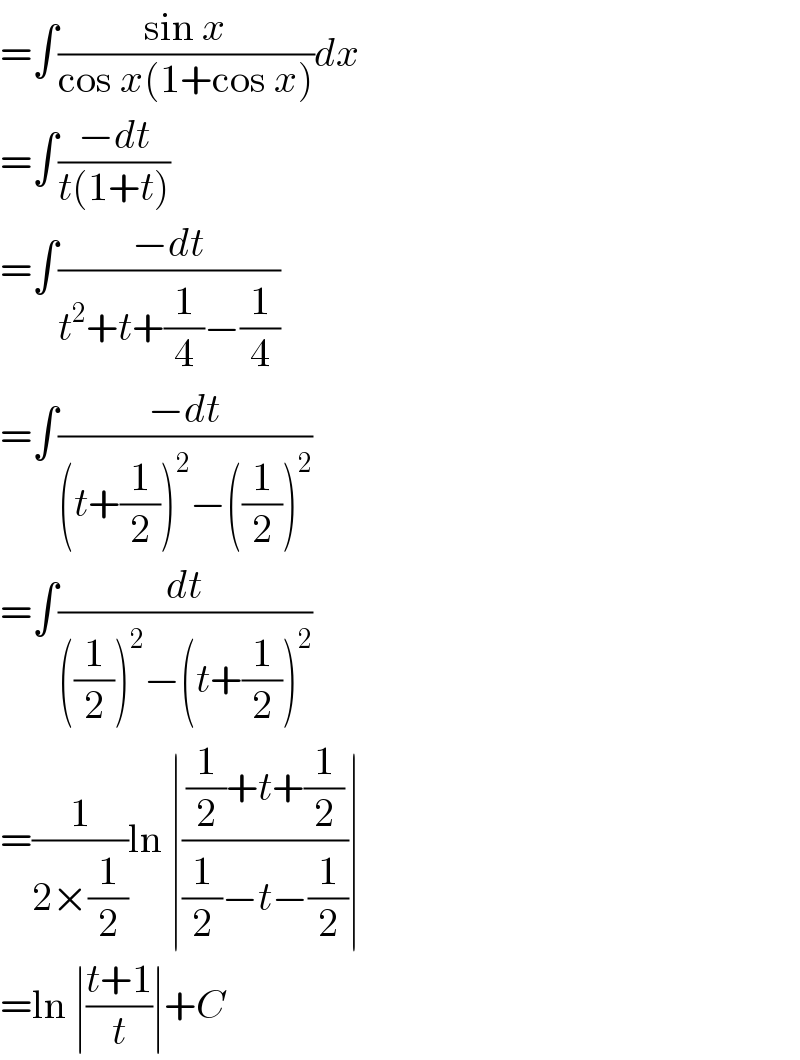
$$=\int\frac{\mathrm{sin}\:{x}}{\mathrm{cos}\:{x}\left(\mathrm{1}+\mathrm{cos}\:{x}\right)}{dx} \\ $$$$=\int\frac{−{dt}}{{t}\left(\mathrm{1}+{t}\right)} \\ $$$$=\int\frac{−{dt}}{{t}^{\mathrm{2}} +{t}+\frac{\mathrm{1}}{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{4}}} \\ $$$$=\int\frac{−{dt}}{\left({t}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} −\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} } \\ $$$$=\int\frac{{dt}}{\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} −\left({t}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}×\frac{\mathrm{1}}{\mathrm{2}}}\mathrm{ln}\:\mid\frac{\frac{\mathrm{1}}{\mathrm{2}}+{t}+\frac{\mathrm{1}}{\mathrm{2}}}{\frac{\mathrm{1}}{\mathrm{2}}−{t}−\frac{\mathrm{1}}{\mathrm{2}}}\mid \\ $$$$=\mathrm{ln}\:\mid\frac{{t}+\mathrm{1}}{{t}}\mid+{C} \\ $$
