Question Number 123971 by Khalmohmmad last updated on 29/Nov/20

$$\mathrm{tan}\:{x}=−\frac{\sqrt{\mathrm{39}}}{\mathrm{3}} \\ $$$$\mathrm{cos}{x}=? \\ $$
Commented by mr W last updated on 29/Nov/20
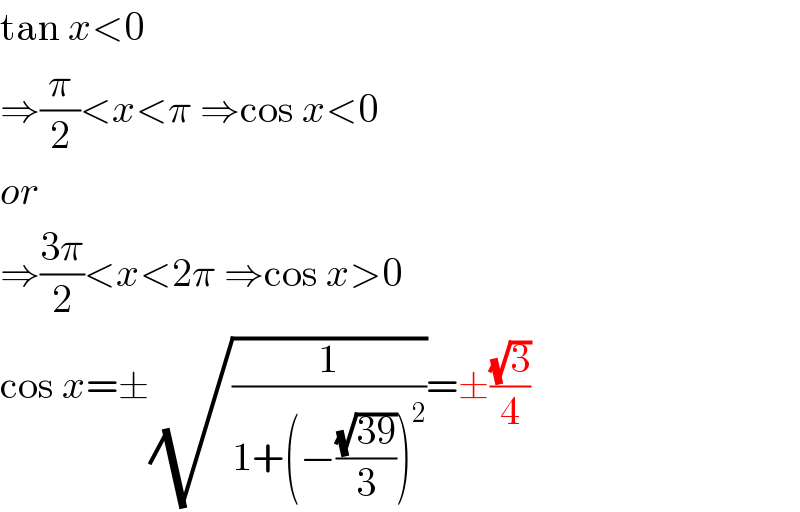
$$\mathrm{tan}\:{x}<\mathrm{0} \\ $$$$\Rightarrow\frac{\pi}{\mathrm{2}}<{x}<\pi\:\Rightarrow\mathrm{cos}\:{x}<\mathrm{0} \\ $$$${or} \\ $$$$\Rightarrow\frac{\mathrm{3}\pi}{\mathrm{2}}<{x}<\mathrm{2}\pi\:\Rightarrow\mathrm{cos}\:{x}>\mathrm{0} \\ $$$$\mathrm{cos}\:{x}=\pm\sqrt{\frac{\mathrm{1}}{\mathrm{1}+\left(−\frac{\sqrt{\mathrm{39}}}{\mathrm{3}}\right)^{\mathrm{2}} }}=\pm\frac{\sqrt{\mathrm{3}}}{\mathrm{4}} \\ $$
Answered by Dwaipayan Shikari last updated on 30/Nov/20
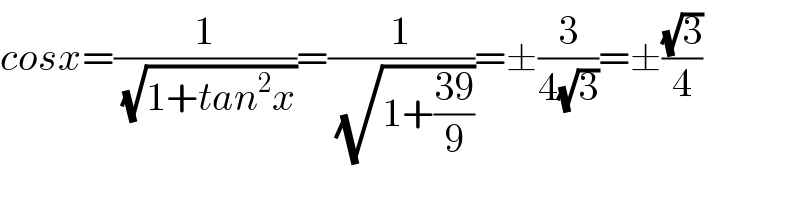
$${cosx}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+{tan}^{\mathrm{2}} {x}}}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+\frac{\mathrm{39}}{\mathrm{9}}}}=\pm\frac{\mathrm{3}}{\mathrm{4}\sqrt{\mathrm{3}}}=\pm\frac{\sqrt{\mathrm{3}}}{\mathrm{4}} \\ $$
Answered by MJS_new last updated on 29/Nov/20
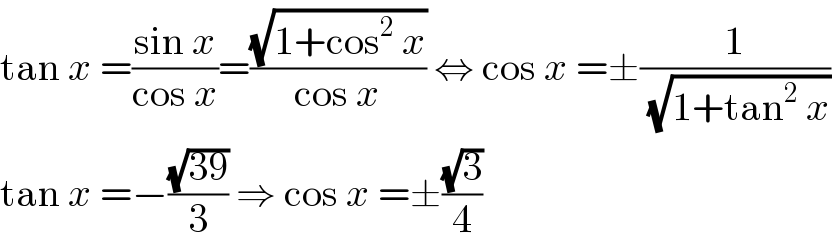
$$\mathrm{tan}\:{x}\:=\frac{\mathrm{sin}\:{x}}{\mathrm{cos}\:{x}}=\frac{\sqrt{\mathrm{1}+\mathrm{cos}^{\mathrm{2}} \:{x}}}{\mathrm{cos}\:{x}}\:\Leftrightarrow\:\mathrm{cos}\:{x}\:=\pm\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \:{x}}} \\ $$$$\mathrm{tan}\:{x}\:=−\frac{\sqrt{\mathrm{39}}}{\mathrm{3}}\:\Rightarrow\:\mathrm{cos}\:{x}\:=\pm\frac{\sqrt{\mathrm{3}}}{\mathrm{4}} \\ $$
