Question Number 94718 by john santu last updated on 20/May/20

$$\int\:\sqrt{\mathrm{tan}\:\mathrm{x}}\:\mathrm{dx}\:= \\ $$$$\int\frac{\sqrt{\mathrm{tan}\:\mathrm{x}}+\sqrt{\mathrm{cot}\:\mathrm{x}}}{\mathrm{2}}\:\mathrm{dx}\:+\:\int\:\frac{\sqrt{\mathrm{tan}\:\mathrm{x}}−\sqrt{\mathrm{cot}\:\mathrm{x}}}{\mathrm{2}}\:\mathrm{dx} \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}\:}\int\:\frac{\mathrm{sin}\:\mathrm{x}+\mathrm{cos}\:\mathrm{x}}{\:\sqrt{\mathrm{sin}\:\mathrm{2x}}}\:\mathrm{dx}\:+\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}\:}\int\:\frac{\mathrm{sin}\:\mathrm{x}−\mathrm{cos}\:\mathrm{x}}{\:\sqrt{\mathrm{sin}\:\mathrm{2x}}}\:\mathrm{dx} \\ $$$$=\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}\:}\int\:\frac{\mathrm{sin}\:\mathrm{x}+\mathrm{cos}\:\mathrm{x}}{\:\sqrt{\mathrm{1}−\left(\mathrm{sin}\:\mathrm{x}−\mathrm{cos}\:\mathrm{x}\right)^{\mathrm{2}} }}\:\mathrm{dx}\:+\: \\ $$$$\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\:\int\:\frac{\mathrm{sin}\:\mathrm{x}−\mathrm{cos}\:\mathrm{x}}{\:\sqrt{\left(\mathrm{sin}\:\mathrm{x}+\mathrm{cos}\:\mathrm{x}\right)^{\mathrm{2}} −\mathrm{1}}}\:\mathrm{dx}\: \\ $$$$=\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}\:}\int\:\frac{\mathrm{dt}}{\:\sqrt{\mathrm{1}−\mathrm{t}^{\mathrm{2}} }}\:+\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}\:}\int\:\frac{−\mathrm{du}}{\:\sqrt{\mathrm{u}^{\mathrm{2}} −\mathrm{1}}} \\ $$$$=\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}\:}\mathrm{sin}^{−\mathrm{1}} \left(\mathrm{t}\right)\:−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\:\mathrm{ln}\left(\mathrm{u}+\sqrt{\mathrm{u}^{\mathrm{2}} −\mathrm{1}}\right)\:+\mathrm{c} \\ $$$$=\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\:\mathrm{sin}^{−\mathrm{1}} \left(\mathrm{sin}\:\mathrm{x}−\mathrm{cos}\:\mathrm{x}\right)− \\ $$$$\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\:\mathrm{ln}\:\left(\mathrm{sin}\:\mathrm{x}+\mathrm{cos}\:\mathrm{x}+\sqrt{\mathrm{sin}\:\mathrm{2x}}\right)\:+\:\mathrm{c}\: \\ $$$$\mathrm{where}\:\mathrm{t}\:=\:\mathrm{sin}\:\mathrm{x}−\mathrm{cos}\:\mathrm{x}\:;\: \\ $$$$\mathrm{u}\:=\:\mathrm{sin}\:\mathrm{x}+\mathrm{cos}\:\mathrm{x}\: \\ $$
Commented by i jagooll last updated on 20/May/20

$$\mathrm{waww}\:\mathrm{simple} \\ $$
Commented by MJS last updated on 20/May/20
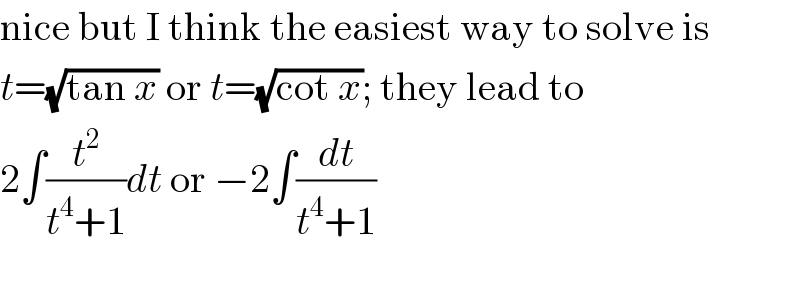
$$\mathrm{nice}\:\mathrm{but}\:\mathrm{I}\:\mathrm{think}\:\mathrm{the}\:\mathrm{easiest}\:\mathrm{way}\:\mathrm{to}\:\mathrm{solve}\:\mathrm{is} \\ $$$${t}=\sqrt{\mathrm{tan}\:{x}}\:\mathrm{or}\:{t}=\sqrt{\mathrm{cot}\:{x}};\:\mathrm{they}\:\mathrm{lead}\:\mathrm{to} \\ $$$$\mathrm{2}\int\frac{{t}^{\mathrm{2}} }{{t}^{\mathrm{4}} +\mathrm{1}}{dt}\:\mathrm{or}\:−\mathrm{2}\int\frac{{dt}}{{t}^{\mathrm{4}} +\mathrm{1}} \\ $$$$ \\ $$
Commented by peter frank last updated on 20/May/20

$$\mathrm{good} \\ $$
Commented by peter frank last updated on 20/May/20

$$\mathrm{good} \\ $$
