Question Number 149112 by bramlexs22 last updated on 03/Aug/21

$$\:\varphi\:=\:\int\:\mathrm{tan}\:\left(\mathrm{x}+\frac{\pi}{\mathrm{3}}\right)\mathrm{tan}\:\mathrm{3x}\:\mathrm{tan}\:\left(\mathrm{2x}−\frac{\pi}{\mathrm{3}}\right)\:\mathrm{dx}\:=? \\ $$
Commented by som(math1967) last updated on 03/Aug/21
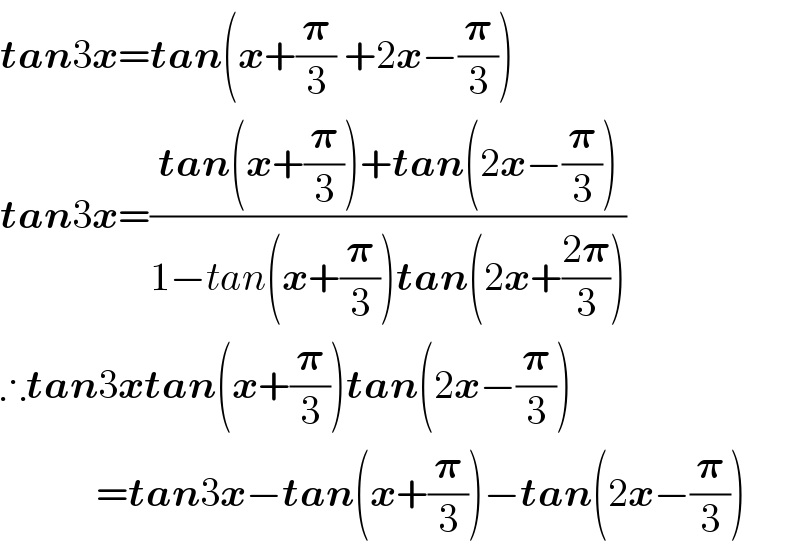
$$\boldsymbol{{tan}}\mathrm{3}\boldsymbol{{x}}=\boldsymbol{{tan}}\left(\boldsymbol{{x}}+\frac{\boldsymbol{\pi}}{\mathrm{3}}\:+\mathrm{2}\boldsymbol{{x}}−\frac{\boldsymbol{\pi}}{\mathrm{3}}\right) \\ $$$$\boldsymbol{{tan}}\mathrm{3}\boldsymbol{{x}}=\frac{\boldsymbol{{tan}}\left(\boldsymbol{{x}}+\frac{\boldsymbol{\pi}}{\mathrm{3}}\right)+\boldsymbol{{tan}}\left(\mathrm{2}\boldsymbol{{x}}−\frac{\boldsymbol{\pi}}{\mathrm{3}}\right)}{\mathrm{1}−{tan}\left(\boldsymbol{{x}}+\frac{\boldsymbol{\pi}}{\mathrm{3}}\right)\boldsymbol{{tan}}\left(\mathrm{2}\boldsymbol{{x}}+\frac{\mathrm{2}\boldsymbol{\pi}}{\mathrm{3}}\right)} \\ $$$$\therefore\boldsymbol{{tan}}\mathrm{3}\boldsymbol{{xtan}}\left(\boldsymbol{{x}}+\frac{\boldsymbol{\pi}}{\mathrm{3}}\right)\boldsymbol{{tan}}\left(\mathrm{2}\boldsymbol{{x}}−\frac{\boldsymbol{\pi}}{\mathrm{3}}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=\boldsymbol{{tan}}\mathrm{3}\boldsymbol{{x}}−\boldsymbol{{tan}}\left(\boldsymbol{{x}}+\frac{\boldsymbol{\pi}}{\mathrm{3}}\right)−\boldsymbol{{tan}}\left(\mathrm{2}\boldsymbol{{x}}−\frac{\boldsymbol{\pi}}{\mathrm{3}}\right) \\ $$
Commented by bramlexs22 last updated on 03/Aug/21

$$\mathrm{yes}\:\mathrm{thanks} \\ $$
