Question Number 144431 by imjagoll last updated on 25/Jun/21
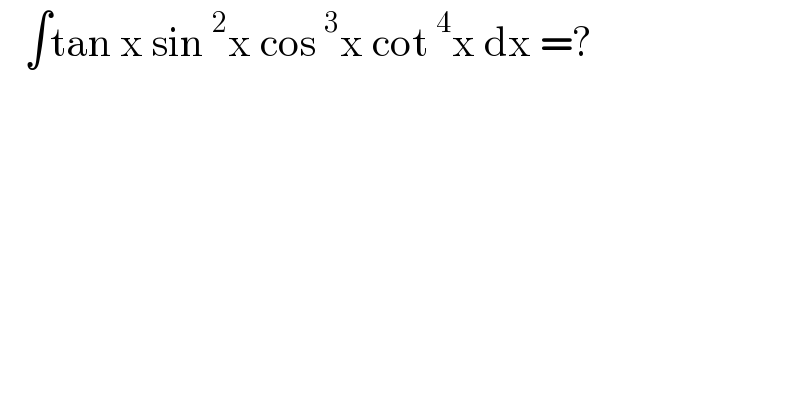
$$\:\:\:\int\mathrm{tan}\:\mathrm{x}\:\mathrm{sin}\:^{\mathrm{2}} \mathrm{x}\:\mathrm{cos}\:^{\mathrm{3}} \mathrm{x}\:\mathrm{cot}\:^{\mathrm{4}} \mathrm{x}\:\mathrm{dx}\:=? \\ $$
Answered by iloveisrael last updated on 25/Jun/21
![∫ ((cos^6 x sin x)/(sin^2 x)) dx = ∫ ((cos^6 x sin x)/(1−cos^2 x)) dx = ∫(u^6 /(u^2 −1)) du = ∫ ((u^4 (u^2 −1)+u^2 (u^2 −1)+u^2 −1+1)/(u^2 −1)) du = ∫(u^4 +u^2 +1+(1/2)[(1/(u−1))−(1/(u+1))])du =(1/5)u^5 +(1/3)u^3 +u+(1/2)ln ∣((u−1)/(u+1))∣+c = ((cos^5 x)/5)+((cos^3 x)/3)+cos x+(1/2)ln ∣((cos x−1)/(cos x+1))∣+c](https://www.tinkutara.com/question/Q144435.png)
$$\:\int\:\frac{\mathrm{cos}\:^{\mathrm{6}} \mathrm{x}\:\mathrm{sin}\:\mathrm{x}}{\mathrm{sin}\:^{\mathrm{2}} \mathrm{x}}\:\mathrm{dx}\:=\:\int\:\frac{\mathrm{cos}\:^{\mathrm{6}} \mathrm{x}\:\mathrm{sin}\:\mathrm{x}}{\mathrm{1}−\mathrm{cos}\:^{\mathrm{2}} \mathrm{x}}\:\mathrm{dx} \\ $$$$=\:\int\frac{\mathrm{u}^{\mathrm{6}} }{\mathrm{u}^{\mathrm{2}} −\mathrm{1}}\:\mathrm{du}\:=\:\int\:\frac{\mathrm{u}^{\mathrm{4}} \left(\mathrm{u}^{\mathrm{2}} −\mathrm{1}\right)+\mathrm{u}^{\mathrm{2}} \left(\mathrm{u}^{\mathrm{2}} −\mathrm{1}\right)+\mathrm{u}^{\mathrm{2}} −\mathrm{1}+\mathrm{1}}{\mathrm{u}^{\mathrm{2}} −\mathrm{1}}\:\mathrm{du} \\ $$$$=\:\int\left(\mathrm{u}^{\mathrm{4}} +\mathrm{u}^{\mathrm{2}} +\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}\left[\frac{\mathrm{1}}{\mathrm{u}−\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{u}+\mathrm{1}}\right]\right)\mathrm{du} \\ $$$$=\frac{\mathrm{1}}{\mathrm{5}}\mathrm{u}^{\mathrm{5}} +\frac{\mathrm{1}}{\mathrm{3}}\mathrm{u}^{\mathrm{3}} +\mathrm{u}+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\mid\frac{\mathrm{u}−\mathrm{1}}{\mathrm{u}+\mathrm{1}}\mid+\mathrm{c} \\ $$$$=\:\frac{\mathrm{cos}\:^{\mathrm{5}} \mathrm{x}}{\mathrm{5}}+\frac{\mathrm{cos}\:^{\mathrm{3}} \mathrm{x}}{\mathrm{3}}+\mathrm{cos}\:\mathrm{x}+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\mid\frac{\mathrm{cos}\:\mathrm{x}−\mathrm{1}}{\mathrm{cos}\:\mathrm{x}+\mathrm{1}}\mid+\mathrm{c}\:\: \\ $$
