Question Number 130809 by bemath last updated on 29/Jan/21
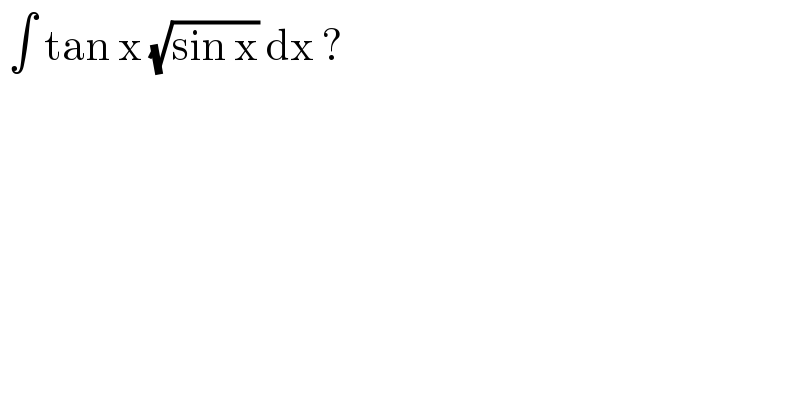
$$\:\int\:\mathrm{tan}\:\mathrm{x}\:\sqrt{\mathrm{sin}\:\mathrm{x}}\:\mathrm{dx}\:? \\ $$
Answered by EDWIN88 last updated on 29/Jan/21
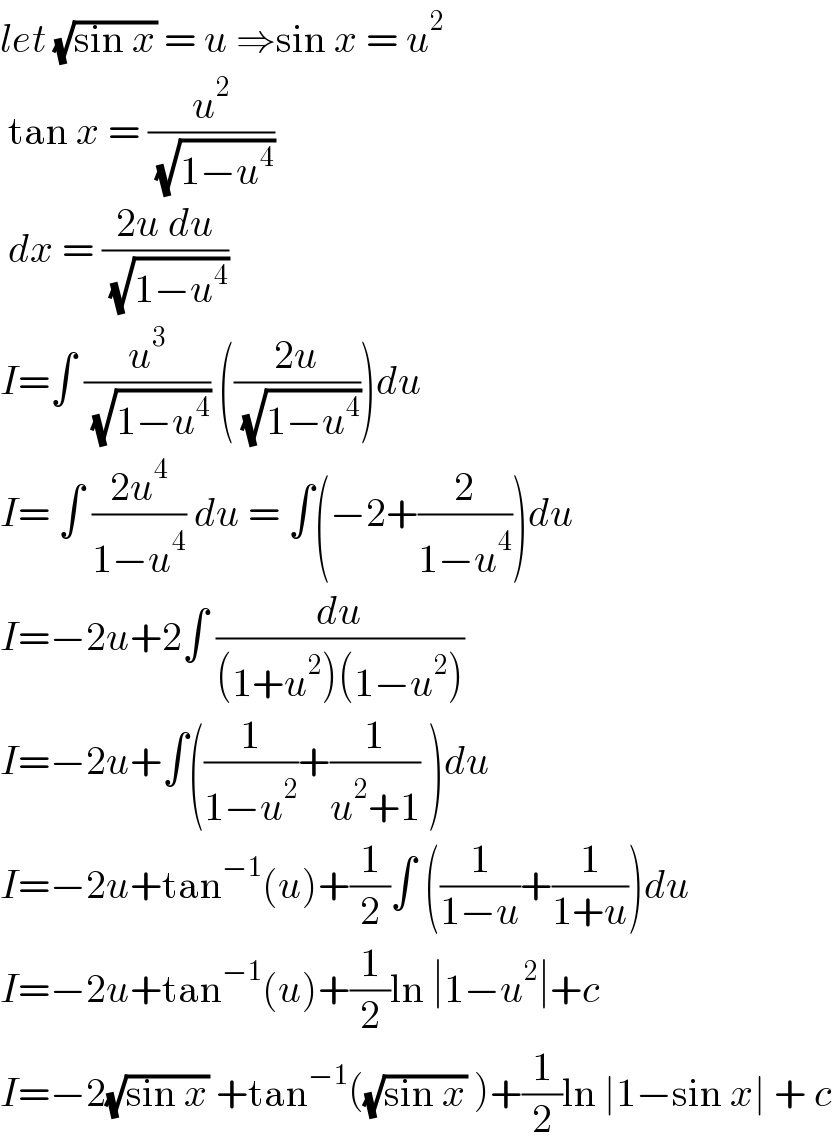
$${let}\:\sqrt{\mathrm{sin}\:{x}}\:=\:{u}\:\Rightarrow\mathrm{sin}\:{x}\:=\:{u}^{\mathrm{2}} \\ $$$$\:\mathrm{tan}\:{x}\:=\:\frac{{u}^{\mathrm{2}} }{\:\sqrt{\mathrm{1}−{u}^{\mathrm{4}} }}\: \\ $$$$\:{dx}\:=\:\frac{\mathrm{2}{u}\:{du}}{\:\sqrt{\mathrm{1}−{u}^{\mathrm{4}} }} \\ $$$${I}=\int\:\frac{{u}^{\mathrm{3}} }{\:\sqrt{\mathrm{1}−{u}^{\mathrm{4}} }}\:\left(\frac{\mathrm{2}{u}}{\:\sqrt{\mathrm{1}−{u}^{\mathrm{4}} }}\right){du} \\ $$$${I}=\:\int\:\frac{\mathrm{2}{u}^{\mathrm{4}} }{\mathrm{1}−{u}^{\mathrm{4}} }\:{du}\:=\:\int\left(−\mathrm{2}+\frac{\mathrm{2}}{\mathrm{1}−{u}^{\mathrm{4}} }\right){du} \\ $$$${I}=−\mathrm{2}{u}+\mathrm{2}\int\:\frac{{du}}{\left(\mathrm{1}+{u}^{\mathrm{2}} \right)\left(\mathrm{1}−{u}^{\mathrm{2}} \right)} \\ $$$${I}=−\mathrm{2}{u}+\int\left(\frac{\mathrm{1}}{\mathrm{1}−{u}^{\mathrm{2}} }+\frac{\mathrm{1}}{{u}^{\mathrm{2}} +\mathrm{1}}\:\right){du} \\ $$$${I}=−\mathrm{2}{u}+\mathrm{tan}^{−\mathrm{1}} \left({u}\right)+\frac{\mathrm{1}}{\mathrm{2}}\int\:\left(\frac{\mathrm{1}}{\mathrm{1}−{u}}+\frac{\mathrm{1}}{\mathrm{1}+{u}}\right){du} \\ $$$${I}=−\mathrm{2}{u}+\mathrm{tan}^{−\mathrm{1}} \left({u}\right)+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\mid\mathrm{1}−{u}^{\mathrm{2}} \mid+{c} \\ $$$${I}=−\mathrm{2}\sqrt{\mathrm{sin}\:{x}}\:+\mathrm{tan}^{−\mathrm{1}} \left(\sqrt{\mathrm{sin}\:{x}}\:\right)+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\mid\mathrm{1}−\mathrm{sin}\:{x}\mid\:+\:{c} \\ $$
