Question Number 127368 by I want to learn more last updated on 29/Dec/20
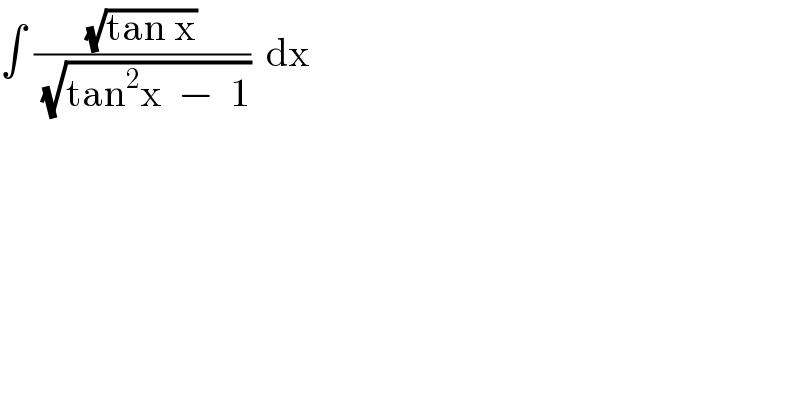
$$\int\:\frac{\sqrt{\mathrm{tan}\:\mathrm{x}}}{\:\sqrt{\mathrm{tan}^{\mathrm{2}} \mathrm{x}\:\:−\:\:\mathrm{1}}}\:\:\mathrm{dx} \\ $$
Answered by liberty last updated on 29/Dec/20

$$\:{let}\:\rightarrow\begin{cases}{\mathrm{tan}\:{x}\:\geqslant\mathrm{0}}\\{\mathrm{tan}^{\mathrm{2}} \:{x}\:>\:\mathrm{1}}\end{cases} \\ $$$${L}\:=\:\int\:\sqrt{\frac{\frac{\mathrm{sin}\:{x}}{\mathrm{cos}\:{x}}}{\frac{\mathrm{sin}\:^{\mathrm{2}} {x}−\mathrm{cos}\:^{\mathrm{2}} {x}}{\mathrm{cos}\:^{\mathrm{2}} {x}}}}\:{dx}\: \\ $$$${L}\:=\:\int\:\sqrt{\frac{\mathrm{sin}\:{x}\:\mathrm{cos}\:{x}}{\mathrm{sin}\:^{\mathrm{2}} {x}−\mathrm{cos}\:^{\mathrm{2}} {x}}}\:{dx}\:=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\int\:\sqrt{−\mathrm{tan}\:\mathrm{2}{x}}\:{dx} \\ $$$${L}\:=\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\:\int\:\sqrt{\mathrm{tan}\:\left(−\mathrm{2}{x}\right)}\:{dx} \\ $$$${putting}\:{z}\:=\:−\mathrm{2}{x}\:\Rightarrow{L}\:=\:−\frac{\sqrt{\mathrm{2}}}{\mathrm{4}}\:\int\:\sqrt{\mathrm{tan}\:{z}}\:{dz} \\ $$$${L}\:=\:−\frac{\sqrt{\mathrm{2}}}{\mathrm{4}}\:\left(\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\:\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{tan}\:{z}−\mathrm{1}}{\:\sqrt{\mathrm{2tan}\:{z}}}\right)+\frac{\sqrt{\mathrm{2}}}{\mathrm{4}}\mathrm{ln}\:\mid\:\frac{\mathrm{tan}\:{z}−\sqrt{\mathrm{2tan}\:{z}}\:+\mathrm{1}}{\mathrm{tan}\:{z}+\sqrt{\mathrm{2tan}\:{z}}\:+\mathrm{1}}\:\mid\:+\:{c}\right. \\ $$$${L}=\frac{\mathrm{1}}{\mathrm{4}}\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{tan}\:\mathrm{2}{x}+\mathrm{1}}{\:\sqrt{−\mathrm{2tan}\:\mathrm{2}{x}}}\right)+\frac{\mathrm{1}}{\mathrm{8}}\mathrm{ln}\:\:\mid\frac{\mathrm{tan}\:\mathrm{2}{x}+\sqrt{−\mathrm{2tan}\:\mathrm{2}{x}}−\mathrm{1}}{\mathrm{tan}\:\mathrm{2}{x}−\sqrt{−\mathrm{2tan}\:\mathrm{2}{x}}−\mathrm{1}}\:\mid\:+\:{c} \\ $$$$ \\ $$
Commented by I want to learn more last updated on 29/Dec/20
$$\mathrm{Thanks}\:\mathrm{sir},\:\mathrm{i}\:\mathrm{appreciate}. \\ $$
