Menu Close

tan-x-tan-2x-tan-3x-dx-

Tinku Tara 0 Comments
Pin




Question Number 118541 by bramlexs22 last updated on 18/Oct/20
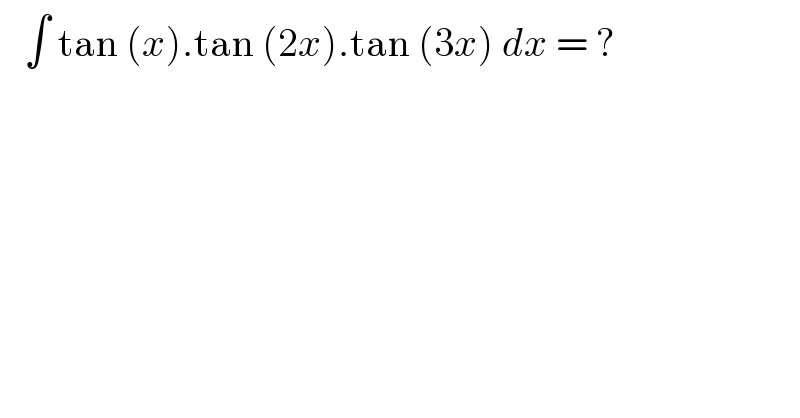
∫ tan (x).tan (2x).tan (3x) dx = ?
$$\:\:\:\int\:\mathrm{tan}\:\left({x}\right).\mathrm{tan}\:\left(\mathrm{2}{x}\right).\mathrm{tan}\:\left(\mathrm{3}{x}\right)\:{dx}\:=\:? \\ $$
Commented by bramlexs22 last updated on 18/Oct/20
thank you all
$${thank}\:{you}\:{all}\: \\ $$
Answered by Lordose last updated on 18/Oct/20
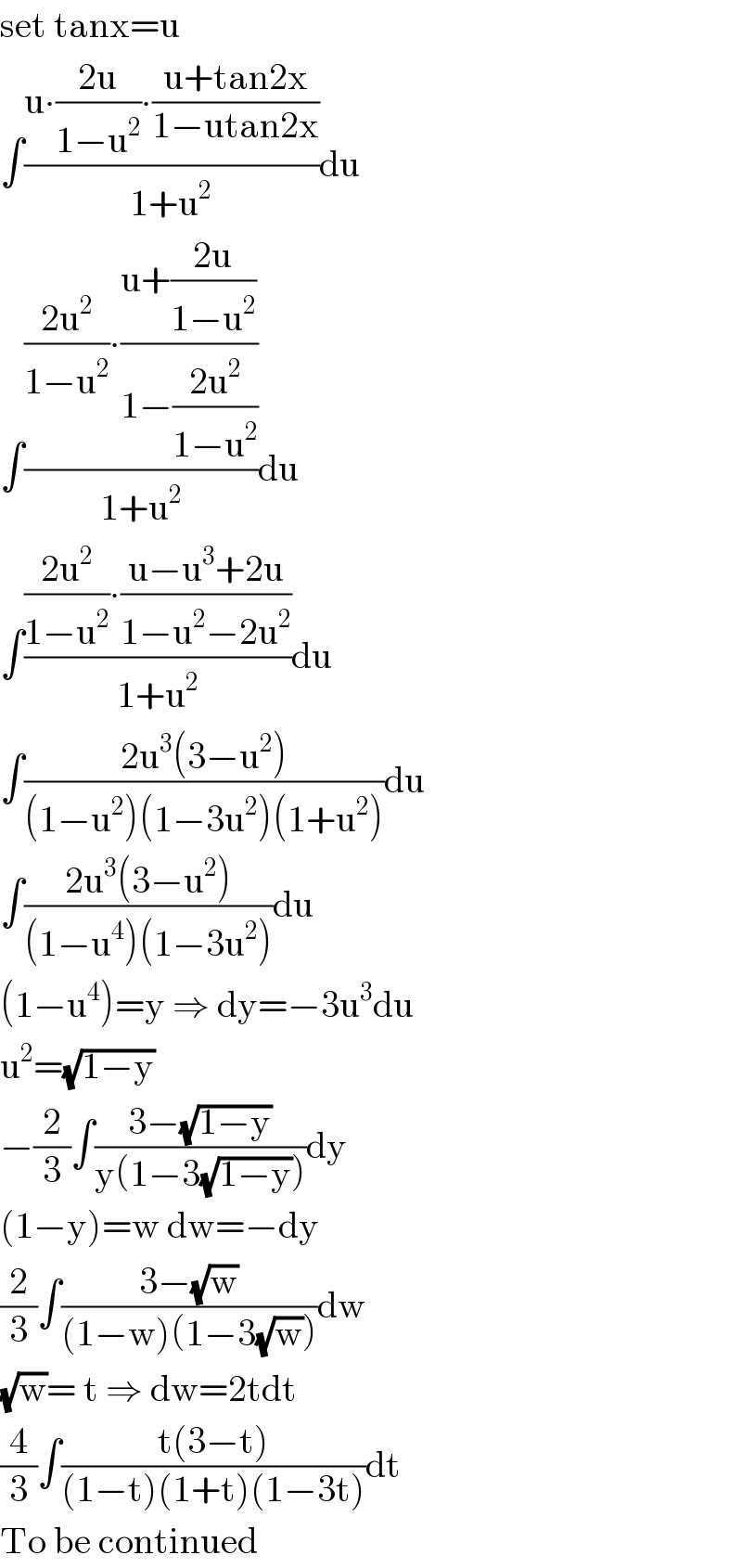
set tanx=u ∫((u∙((2u)/(1−u^2 ))∙((u+tan2x)/(1−utan2x)))/(1+u^2 ))du ∫((((2u^2 )/(1−u^2 ))∙((u+((2u)/(1−u^2 )))/(1−((2u^2 )/(1−u^2 )))))/(1+u^2 ))du ∫((((2u^2 )/(1−u^2 ))∙((u−u^3 +2u)/(1−u^2 −2u^2 )))/(1+u^2 ))du ∫((2u^3 (3−u^2 ))/((1−u^2 )(1−3u^2 )(1+u^2 )))du ∫((2u^3 (3−u^2 ))/((1−u^4 )(1−3u^2 )))du (1−u^4 )=y ⇒ dy=−3u^3 du u^2 =(√(1−y)) −(2/3)∫((3−(√(1−y)))/(y(1−3(√(1−y)))))dy (1−y)=w dw=−dy (2/3)∫((3−(√w))/((1−w)(1−3(√w))))dw (√w)= t ⇒ dw=2tdt (4/3)∫((t(3−t))/((1−t)(1+t)(1−3t)))dt To be continued
$$\mathrm{set}\:\mathrm{tanx}=\mathrm{u} \\ $$$$\int\frac{\mathrm{u}\centerdot\frac{\mathrm{2u}}{\mathrm{1}−\mathrm{u}^{\mathrm{2}} }\centerdot\frac{\mathrm{u}+\mathrm{tan2x}}{\mathrm{1}−\mathrm{utan2x}}}{\mathrm{1}+\mathrm{u}^{\mathrm{2}} }\mathrm{du} \\ $$$$\int\frac{\frac{\mathrm{2u}^{\mathrm{2}} }{\mathrm{1}−\mathrm{u}^{\mathrm{2}} }\centerdot\frac{\mathrm{u}+\frac{\mathrm{2u}}{\mathrm{1}−\mathrm{u}^{\mathrm{2}} }}{\mathrm{1}−\frac{\mathrm{2u}^{\mathrm{2}} }{\mathrm{1}−\mathrm{u}^{\mathrm{2}} }}}{\mathrm{1}+\mathrm{u}^{\mathrm{2}} }\mathrm{du} \\ $$$$\int\frac{\frac{\mathrm{2u}^{\mathrm{2}} }{\mathrm{1}−\mathrm{u}^{\mathrm{2}} }\centerdot\frac{\mathrm{u}−\mathrm{u}^{\mathrm{3}} +\mathrm{2u}}{\mathrm{1}−\mathrm{u}^{\mathrm{2}} −\mathrm{2u}^{\mathrm{2}} }}{\mathrm{1}+\mathrm{u}^{\mathrm{2}} }\mathrm{du} \\ $$$$\int\frac{\mathrm{2u}^{\mathrm{3}} \left(\mathrm{3}−\mathrm{u}^{\mathrm{2}} \right)}{\left(\mathrm{1}−\mathrm{u}^{\mathrm{2}} \right)\left(\mathrm{1}−\mathrm{3u}^{\mathrm{2}} \right)\left(\mathrm{1}+\mathrm{u}^{\mathrm{2}} \right)}\mathrm{du} \\ $$$$\int\frac{\mathrm{2u}^{\mathrm{3}} \left(\mathrm{3}−\mathrm{u}^{\mathrm{2}} \right)}{\left(\mathrm{1}−\mathrm{u}^{\mathrm{4}} \right)\left(\mathrm{1}−\mathrm{3u}^{\mathrm{2}} \right)}\mathrm{du} \\ $$$$\left(\mathrm{1}−\mathrm{u}^{\mathrm{4}} \right)=\mathrm{y}\:\Rightarrow\:\mathrm{dy}=−\mathrm{3u}^{\mathrm{3}} \mathrm{du} \\ $$$$\mathrm{u}^{\mathrm{2}} =\sqrt{\mathrm{1}−\mathrm{y}} \\ $$$$−\frac{\mathrm{2}}{\mathrm{3}}\int\frac{\mathrm{3}−\sqrt{\mathrm{1}−\mathrm{y}}}{\mathrm{y}\left(\mathrm{1}−\mathrm{3}\sqrt{\mathrm{1}−\mathrm{y}}\right)}\mathrm{dy} \\ $$$$\left(\mathrm{1}−\mathrm{y}\right)=\mathrm{w}\:\mathrm{dw}=−\mathrm{dy} \\ $$$$\frac{\mathrm{2}}{\mathrm{3}}\int\frac{\mathrm{3}−\sqrt{\mathrm{w}}}{\left(\mathrm{1}−\mathrm{w}\right)\left(\mathrm{1}−\mathrm{3}\sqrt{\mathrm{w}}\right)}\mathrm{dw} \\ $$$$\sqrt{\mathrm{w}}=\:\mathrm{t}\:\Rightarrow\:\mathrm{dw}=\mathrm{2tdt} \\ $$$$\frac{\mathrm{4}}{\mathrm{3}}\int\frac{\mathrm{t}\left(\mathrm{3}−\mathrm{t}\right)}{\left(\mathrm{1}−\mathrm{t}\right)\left(\mathrm{1}+\mathrm{t}\right)\left(\mathrm{1}−\mathrm{3t}\right)}\mathrm{dt} \\ $$$$\mathrm{To}\:\mathrm{be}\:\mathrm{continued} \\ $$
Answered by TANMAY PANACEA last updated on 18/Oct/20
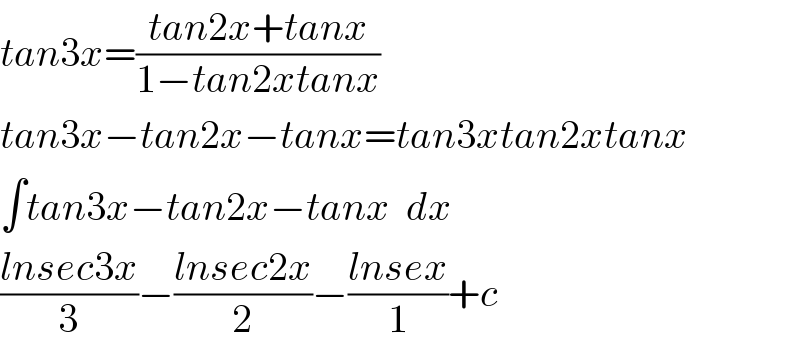
tan3x=((tan2x+tanx)/(1−tan2xtanx)) tan3x−tan2x−tanx=tan3xtan2xtanx ∫tan3x−tan2x−tanx dx ((lnsec3x)/3)−((lnsec2x)/2)−((lnsex)/1)+c
$${tan}\mathrm{3}{x}=\frac{{tan}\mathrm{2}{x}+{tanx}}{\mathrm{1}−{tan}\mathrm{2}{xtanx}} \\ $$$${tan}\mathrm{3}{x}−{tan}\mathrm{2}{x}−{tanx}={tan}\mathrm{3}{xtan}\mathrm{2}{xtanx} \\ $$$$\int{tan}\mathrm{3}{x}−{tan}\mathrm{2}{x}−{tanx}\:\:{dx} \\ $$$$\frac{{lnsec}\mathrm{3}{x}}{\mathrm{3}}−\frac{{lnsec}\mathrm{2}{x}}{\mathrm{2}}−\frac{{lnsex}}{\mathrm{1}}+{c} \\ $$
Commented by mnjuly1970 last updated on 18/Oct/20
very nice solutio sir .. thak you master...
$${very}\:{nice}\:{solutio}\:{sir}\:.. \\ $$$${thak}\:{you}\:{master}… \\ $$
Commented by TANMAY PANACEA last updated on 18/Oct/20
most welcome sir
$${most}\:{welcome}\:{sir} \\ $$
Answered by benjo_mathlover last updated on 18/Oct/20
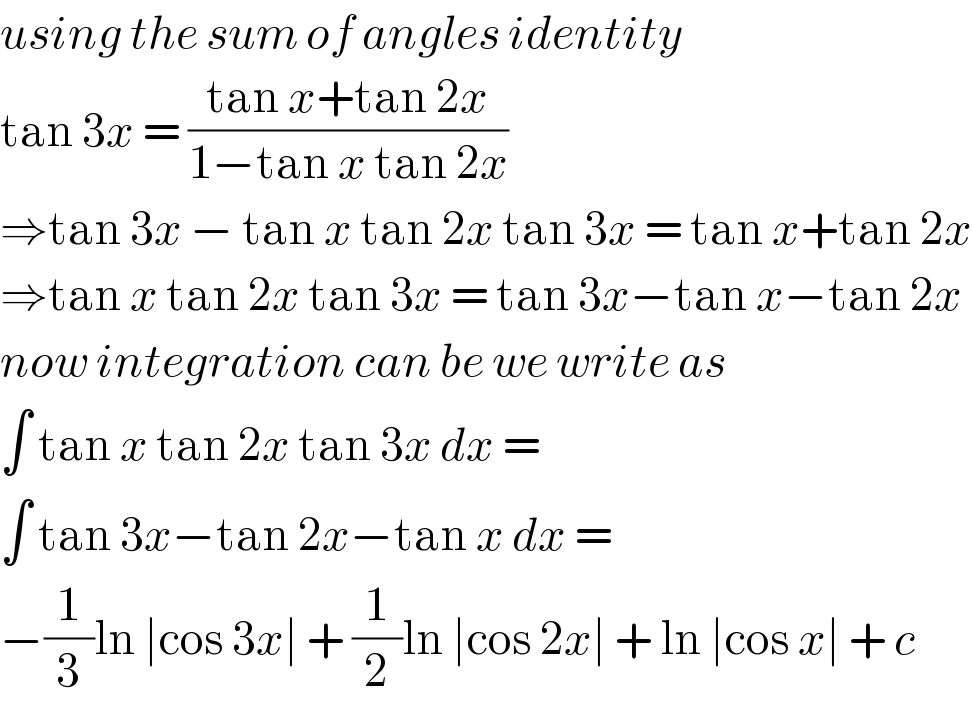
using the sum of angles identity tan 3x = ((tan x+tan 2x)/(1−tan x tan 2x)) ⇒tan 3x − tan x tan 2x tan 3x = tan x+tan 2x ⇒tan x tan 2x tan 3x = tan 3x−tan x−tan 2x now integration can be we write as ∫ tan x tan 2x tan 3x dx = ∫ tan 3x−tan 2x−tan x dx = −(1/3)ln ∣cos 3x∣ + (1/2)ln ∣cos 2x∣ + ln ∣cos x∣ + c
$${using}\:{the}\:{sum}\:{of}\:{angles}\:{identity} \\ $$$$\mathrm{tan}\:\mathrm{3}{x}\:=\:\frac{\mathrm{tan}\:{x}+\mathrm{tan}\:\mathrm{2}{x}}{\mathrm{1}−\mathrm{tan}\:{x}\:\mathrm{tan}\:\mathrm{2}{x}} \\ $$$$\Rightarrow\mathrm{tan}\:\mathrm{3}{x}\:−\:\mathrm{tan}\:{x}\:\mathrm{tan}\:\mathrm{2}{x}\:\mathrm{tan}\:\mathrm{3}{x}\:=\:\mathrm{tan}\:{x}+\mathrm{tan}\:\mathrm{2}{x} \\ $$$$\Rightarrow\mathrm{tan}\:{x}\:\mathrm{tan}\:\mathrm{2}{x}\:\mathrm{tan}\:\mathrm{3}{x}\:=\:\mathrm{tan}\:\mathrm{3}{x}−\mathrm{tan}\:{x}−\mathrm{tan}\:\mathrm{2}{x}\: \\ $$$${now}\:{integration}\:{can}\:{be}\:{we}\:{write}\:{as}\: \\ $$$$\int\:\mathrm{tan}\:{x}\:\mathrm{tan}\:\mathrm{2}{x}\:\mathrm{tan}\:\mathrm{3}{x}\:{dx}\:=\: \\ $$$$\int\:\mathrm{tan}\:\mathrm{3}{x}−\mathrm{tan}\:\mathrm{2}{x}−\mathrm{tan}\:{x}\:{dx}\:= \\ $$$$−\frac{\mathrm{1}}{\mathrm{3}}\mathrm{ln}\:\mid\mathrm{cos}\:\mathrm{3}{x}\mid\:+\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\mid\mathrm{cos}\:\mathrm{2}{x}\mid\:+\:\mathrm{ln}\:\mid\mathrm{cos}\:{x}\mid\:+\:{c} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *