Question Number 20721 by ajfour last updated on 01/Sep/17
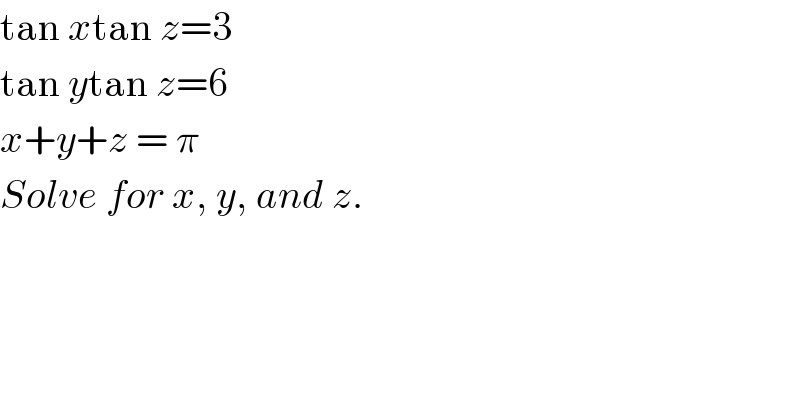
$$\mathrm{tan}\:{x}\mathrm{tan}\:{z}=\mathrm{3} \\ $$$$\mathrm{tan}\:{y}\mathrm{tan}\:{z}=\mathrm{6} \\ $$$${x}+{y}+{z}\:=\:\pi \\ $$$${Solve}\:{for}\:{x},\:{y},\:{and}\:{z}. \\ $$
Answered by sma3l2996 last updated on 02/Sep/17

$${tan}\left({x}+{y}+{z}\right)=\frac{{tan}\left({x}+{y}\right)+{tan}\left({z}\right)}{\mathrm{1}−{tan}\left({x}+{y}\right){tan}\left({z}\right)}=\mathrm{0} \\ $$$$=\frac{\frac{{tanx}+{tany}}{\mathrm{1}−{tanxtany}}+{tanz}}{\mathrm{1}−\frac{{tanx}+{tany}}{\mathrm{1}−{tanxtany}}{tanz}}=\frac{{tanx}+{tany}+{tanz}−{tanxtanytanz}}{\mathrm{1}−\left({tanxtany}+{tanxtanz}+{tanytanz}\right)}=\mathrm{0} \\ $$$${tanx}+{tany}+{tanz}−{tanxtanztanytanz}×\frac{\mathrm{1}}{{tanz}}=\mathrm{0} \\ $$$$\frac{\mathrm{3}}{{tanz}}+\frac{\mathrm{6}}{{tanz}}+{tanz}−\frac{\mathrm{18}}{{tanz}}=\mathrm{0} \\ $$$$\frac{\mathrm{1}}{{tanz}}\left({tan}^{\mathrm{2}} {z}−\mathrm{9}\right)=\mathrm{0}\Leftrightarrow{tanz}=\mathrm{3}\:{or}\:{tanz}=−\mathrm{3}\: \\ $$$${z}={tan}^{−\mathrm{1}} \left(\mathrm{3}\right)+\frac{{k}\pi}{\mathrm{2}}\: \\ $$$${so}\:{tanx}=\frac{\mathrm{3}}{{tanz}}=\frac{\mathrm{3}}{\mathrm{3}}=\mathrm{1}\:{or}\:{tanx}=−\mathrm{1}\: \\ $$$${x}=\frac{\pi}{\mathrm{4}}+\frac{{k}\pi}{\mathrm{2}}\:{and}\:{y}={tan}^{−\mathrm{1}} \left(\mathrm{2}\right)+\frac{{k}\pi}{\mathrm{2}} \\ $$$$ \\ $$
