Question Number 41902 by upadhyayrakhi20@gmail.com last updated on 15/Aug/18
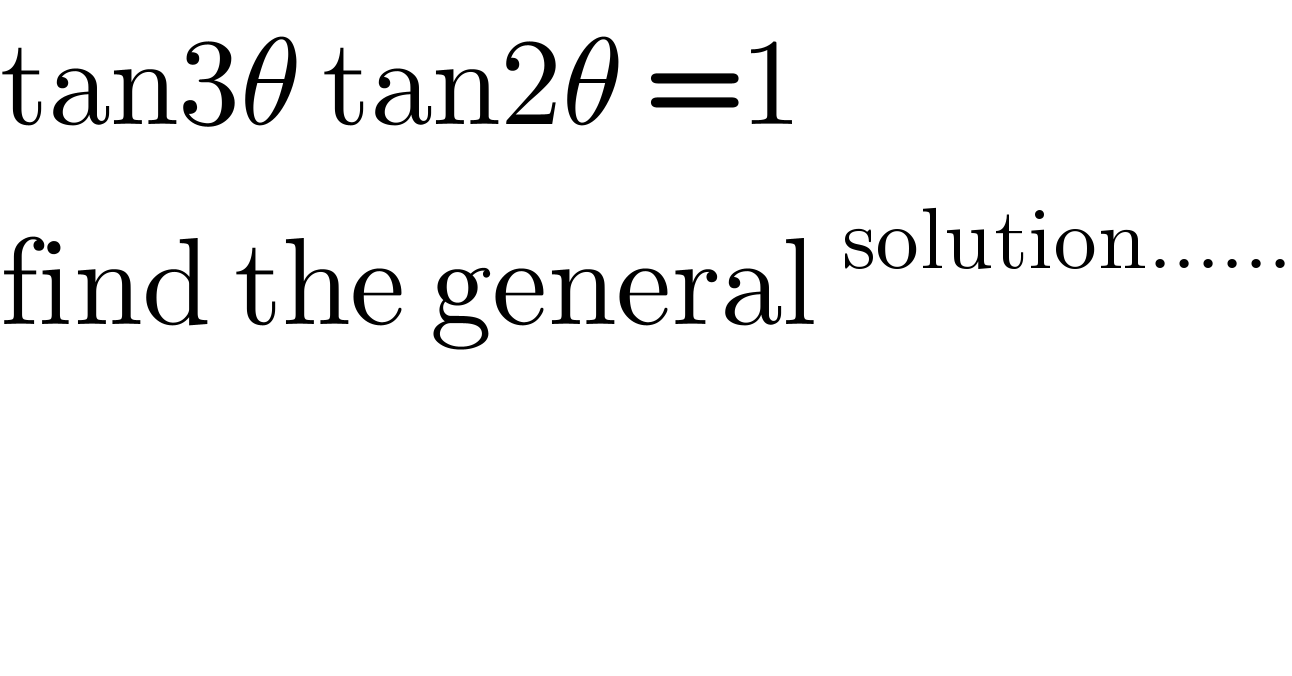
$$\mathrm{tan3}\theta\:\mathrm{tan2}\theta\:=\mathrm{1} \\ $$$$\mathrm{find}\:\mathrm{the}\:\mathrm{general}\:^{\mathrm{solution}……} \\ $$
Answered by MJS last updated on 15/Aug/18
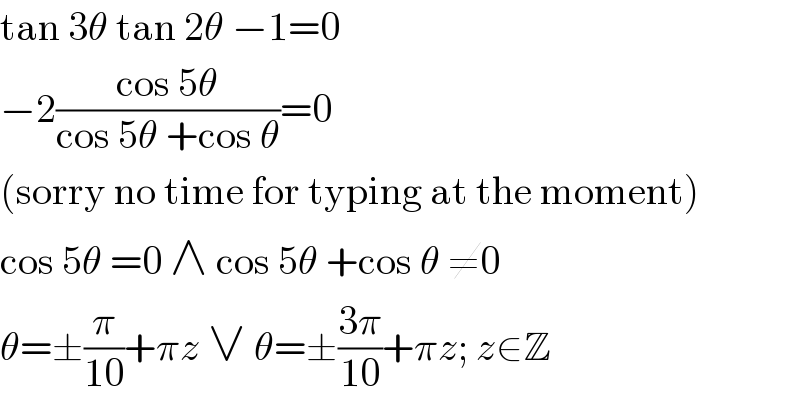
$$\mathrm{tan}\:\mathrm{3}\theta\:\mathrm{tan}\:\mathrm{2}\theta\:−\mathrm{1}=\mathrm{0} \\ $$$$−\mathrm{2}\frac{\mathrm{cos}\:\mathrm{5}\theta}{\mathrm{cos}\:\mathrm{5}\theta\:+\mathrm{cos}\:\theta}=\mathrm{0} \\ $$$$\left(\mathrm{sorry}\:\mathrm{no}\:\mathrm{time}\:\mathrm{for}\:\mathrm{typing}\:\mathrm{at}\:\mathrm{the}\:\mathrm{moment}\right) \\ $$$$\mathrm{cos}\:\mathrm{5}\theta\:=\mathrm{0}\:\wedge\:\mathrm{cos}\:\mathrm{5}\theta\:+\mathrm{cos}\:\theta\:\neq\mathrm{0} \\ $$$$\theta=\pm\frac{\pi}{\mathrm{10}}+\pi{z}\:\vee\:\theta=\pm\frac{\mathrm{3}\pi}{\mathrm{10}}+\pi{z};\:{z}\in\mathbb{Z} \\ $$
